Dynamic programming notes

Dynamical programming

Definition

1. Extremely general algorithm design technique
2. Similar to divide and conquer idea
   1. Build up answer from smaller subproblem
   2. More general than “simple” divide and conquer
3. Generally applies to algorithms where the brute force algorithm would be more exponential

General DP principles

1. Optimal value of the original problem can be computed easily from some subproblem

   OPT(j,w) = max of two subproblems

2. There are only a polynomial # of subproblems

   {(j,w)} for j = 1,…,n and w = 0,…W

3. There is a natural ordering of the subproblems from smallest to the largest such that you can obtain the solutions for a subproblem by only looking at smaller subproblems.

   Considering items {1,2,3} is a smaller problem than considering items {1,2,3,4}

Requirements for DP to apply

1. Optimal value of the original problem can be computed from some similar subproblems
2. There are only a polynomial number of subproblems
3. There is a natural ordering of subproblems, so that you can solve a subproblem by only looking at the small subproblems

DP problems

Subset sum problem

Pseudocode and Run time analysis

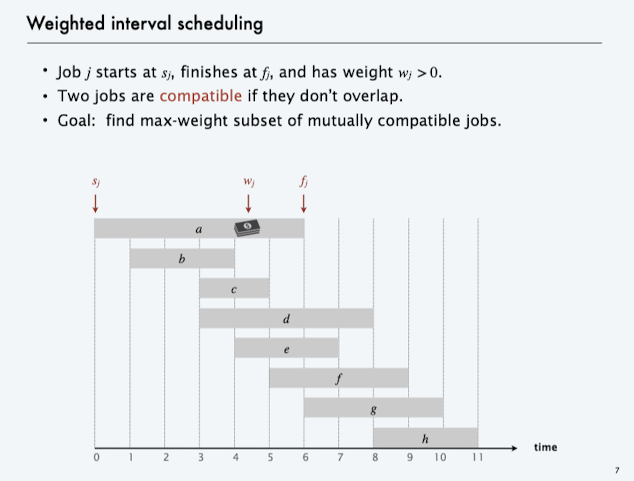
Weighted interval scheduling

0-1 Knapsack problem

Difference with the subset sum: want to maximize value instead of the weight

Noted that the greedy algorithm would not work because we are not allowed to take part of the item

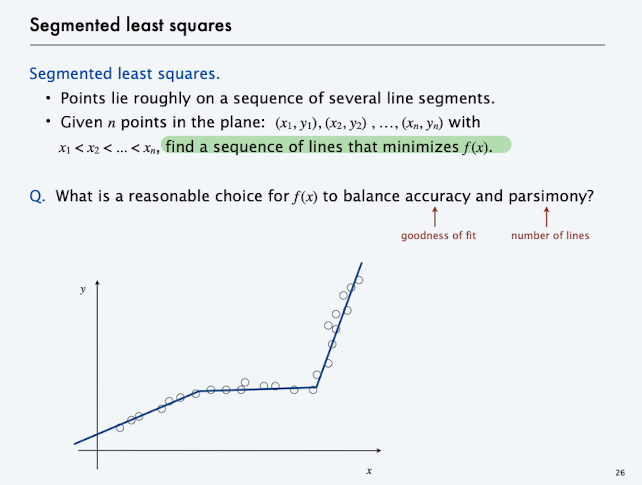
Segmented least squares problem

Internet resources

https://kartikkukreja.wordpress.com/2013/10/21/segmented-least-squares-problem/

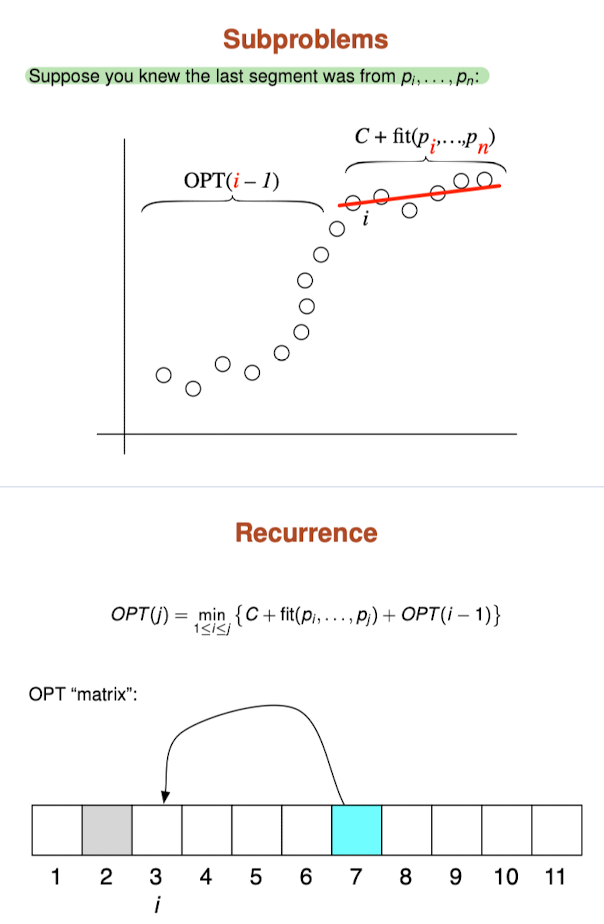
Solution

Notation:

• = minimum cost for points
• = SSE for points

To compute :

• Last segment uses points for some
• Cost =
  • Optimal substructure property (proof via exchange argument)

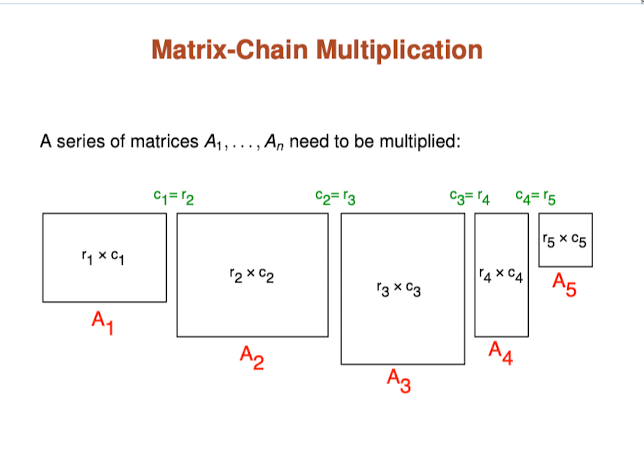
Matrix-chain multiplication

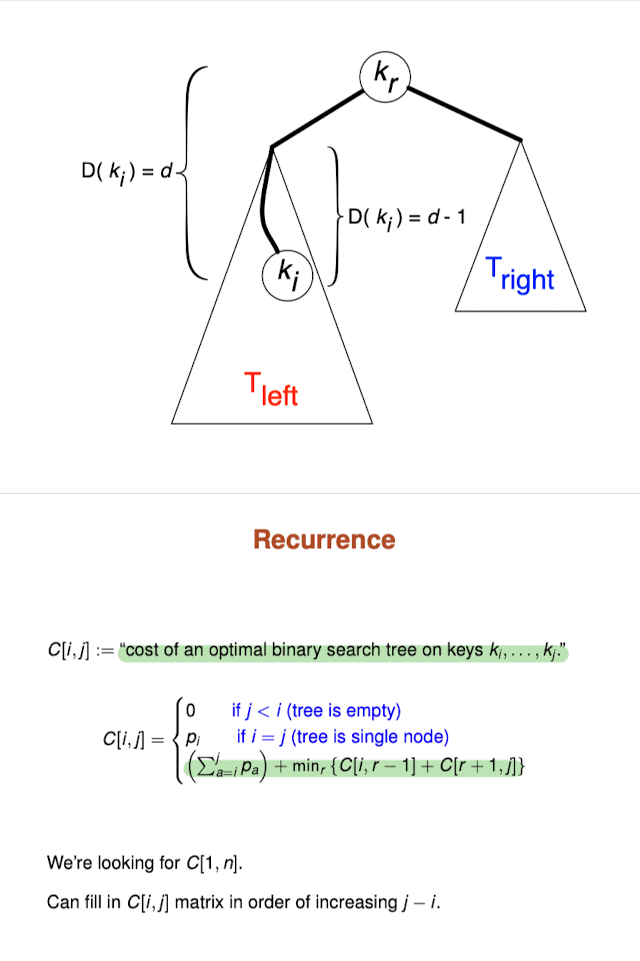
Optimal Binary Search Tree

Maximum subarray problem

Goal: Given an array x of n integer (positive or negative) find a continuous subarray whose sum is maximum

Def: OPT(i) = max sum of any subarray of x whose rightmost index is I:

Goal: max OPT(i)

Word wrap

https://www.geeksforgeeks.org/word-wrap-problem-dp-19/

String alignment problem