Network flow problem notes

Flow network

A flow network is a connected, directed graph G=(V,E)

• Each edge e has a non-negative, integer capacity
• A single source s V
• A single sink
• No edge enters the source and no edge leaves the sink

Assumptions

1. Capacities are integers
2. Every node has one edge adjacent it

Flow

Deifinition: An s-t flow is a function f that assigns a real number to each edge of the node with some constraints

• All the intermediate node, whatever flows in, whatever flows out. No accumulation of flow in the pipe (Balance)
• Capacity constraints, each flow its below or equal the capacity

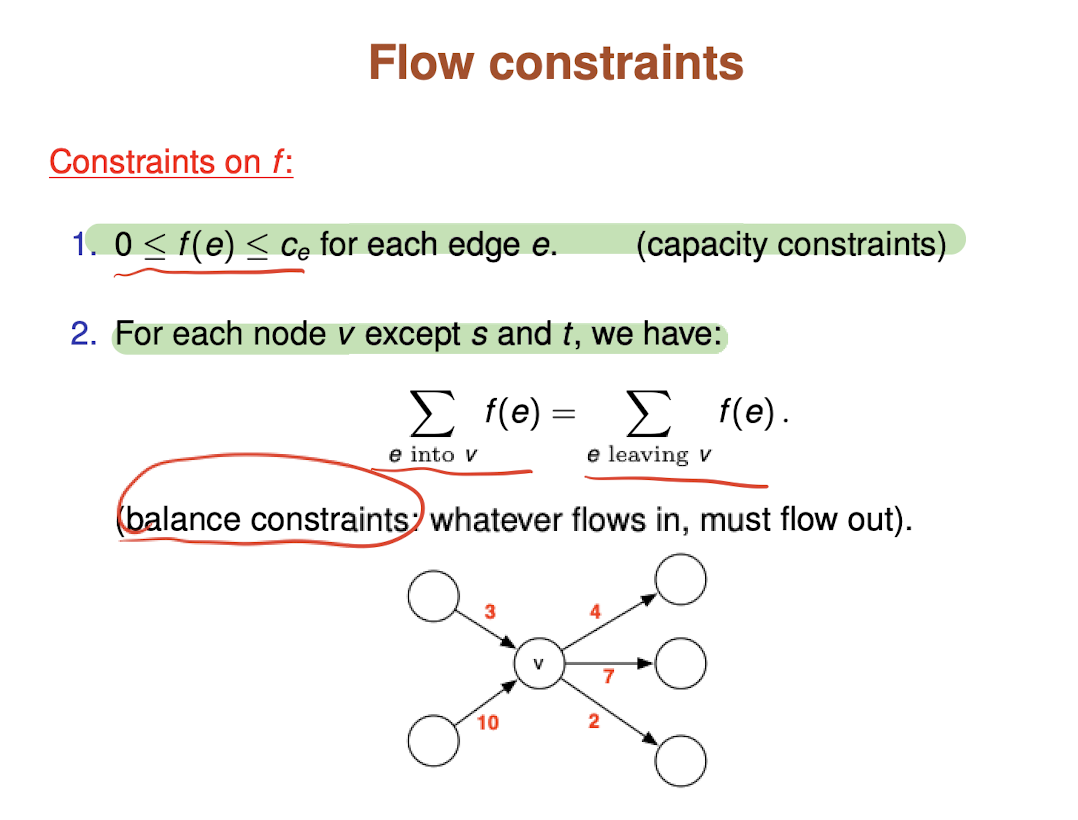
Each edge in the flow graph has a certain flow and capacity specified by the fraction adjacent to each edge. Initially, the flow through each edge is 0 and the capacity is a non negative value

Notation

The value of flow is:

Maximum flow problem

Problem: Given a flow network G, find a flow of maximum possible value.

Ford–Fulkerson method or Ford–Fulkerson algorithm (FFA) is a greedy algorithm that computes the maximum flow in a flow network.

It repeatedly finds augmenting paths through the residual graph and augments the flow until no more augmenting paths can be found.

Dual problem

The dual problem of Max Flow is Min Cut, i.e., by finding the max s-t flow of G, we also simultaneously find the min s-t cut of G, i.e., the set of edges with minimum weight that have to be removed from G so that there is no path from s to t in G.

Greedy start

A sketch of an algorithm:

1. Suppose we let f(e) = 0 for all edges (no flow anywhere)
2. Choose some s-t path and push flow along it up to the capacities. Repeat
3. When we get stuck, we can erase some flow along certain edges

E number of edge 
f(e) flow of edge 
C(e) capacity of edge 

1) Initialize : max_flow = 0  
                f(e) = 0 for every edge 'e' in E 
            
2) Repeat search for an s-t path P while it exists.   
   a) Find if there is a path from s to t using BFS
      or DFS. A path exists if f(e) < C(e) for 
      every edge e on the path.
   b) If no path found, return max_flow.
   c) Else find minimum edge value for path P
        
      // Our flow is limited by least remaining
      // capacity edge on path P.
      (i) flow = min(C(e)- f(e)) for path P ]
             max_flow += flow
      (ii) For all edge e of path increment flow 
             f(e) += flow

3) Return max_flow 

The greedy method results may not be the correct answer.

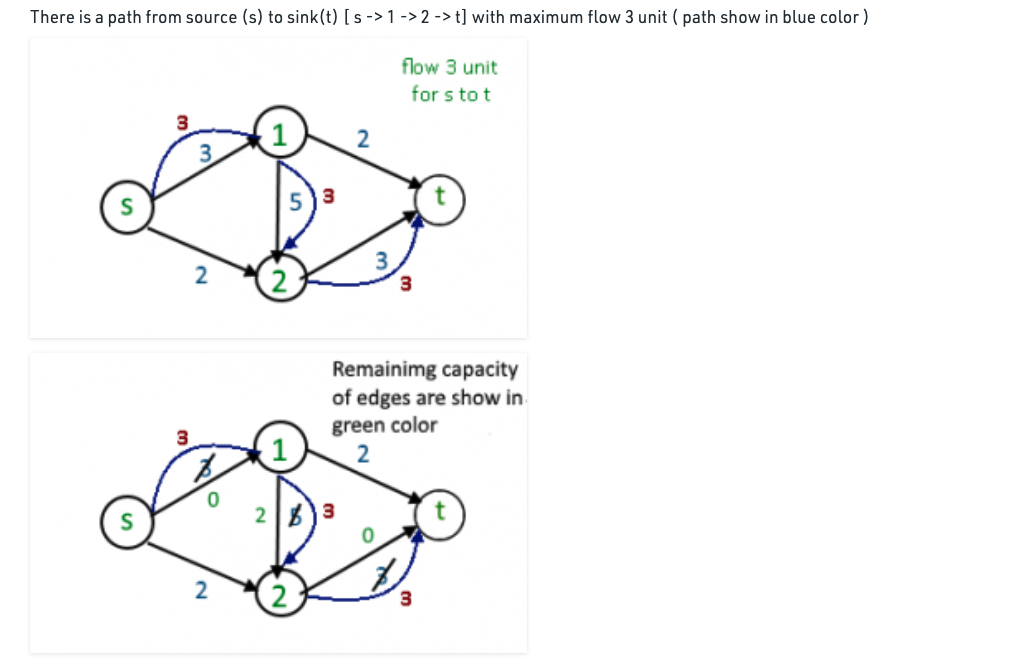
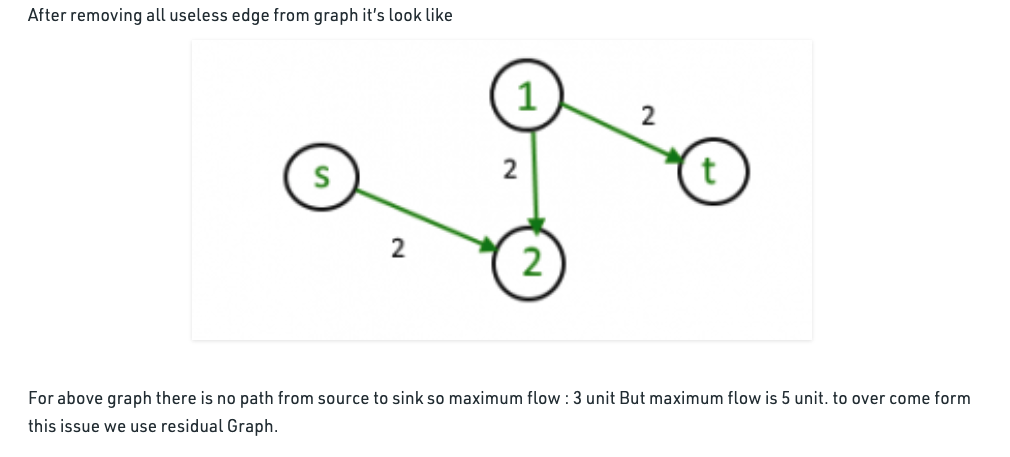
Residual Graph

The previous greedy method may only allow the add operation and in order to obtain the correct answer, the algorithm should allow the undo operation

A key realization to make at this point is that the sum of the sum of the bottlenecks found in each augmenting path is equal to the max-flow

We define a residual graph . Depends on some flow f

1. Contains some nodes as G
2. Forward edges: For each edge e = (u,v) of G for which f(e)<c(e), include an edge e’ = (u,v) in with capacity c(e)-f(e)
3. Backward edges: For each edge e = (u,v) in G with f(e)>0, we include an edge e’ = (v,u) in with capacity f(e)

Noted that, the direction of forward and backward edge are in opposite direction

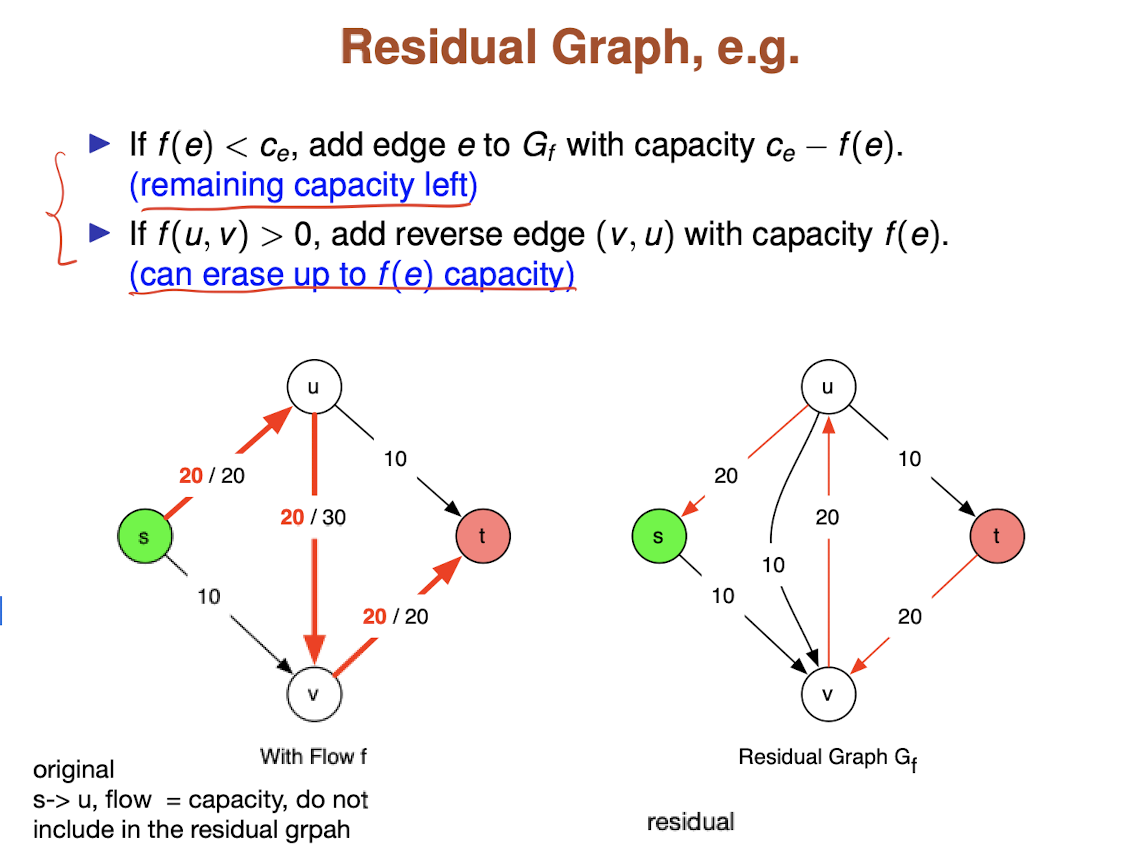
Residual graph

The edges in the residual graph store the remaining capacities of those edges that can be used by future flow(s). At the beginning, these remaining capacities equal to the original capacities as specified in the input flow graph.

A Max Flow algorithm will send flows to use some (or all) of these available capacities, iteratively.

Once the remaining capacity of an edge reaches 0, that edge can no longer admit any more flow.

Augmenting paths

Definition:

An augmenting path is a path of edges in the residual graph with unused capacity greater than zero from the source s to the sink t.

Key thing: it can only flow through edges which aren’t fully saturated yet.

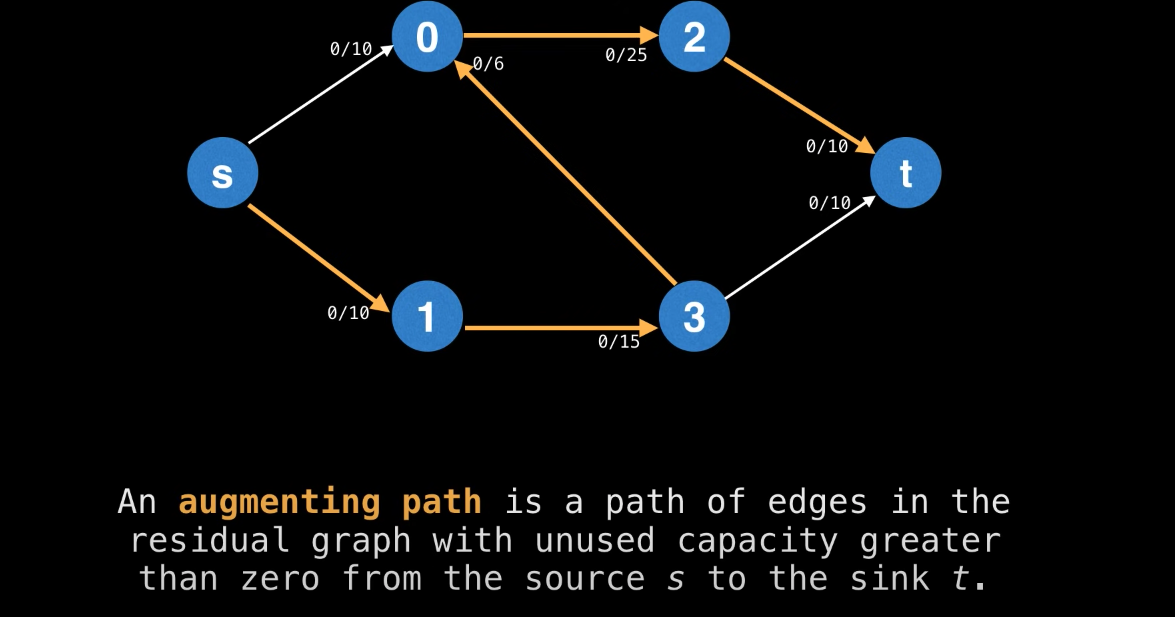
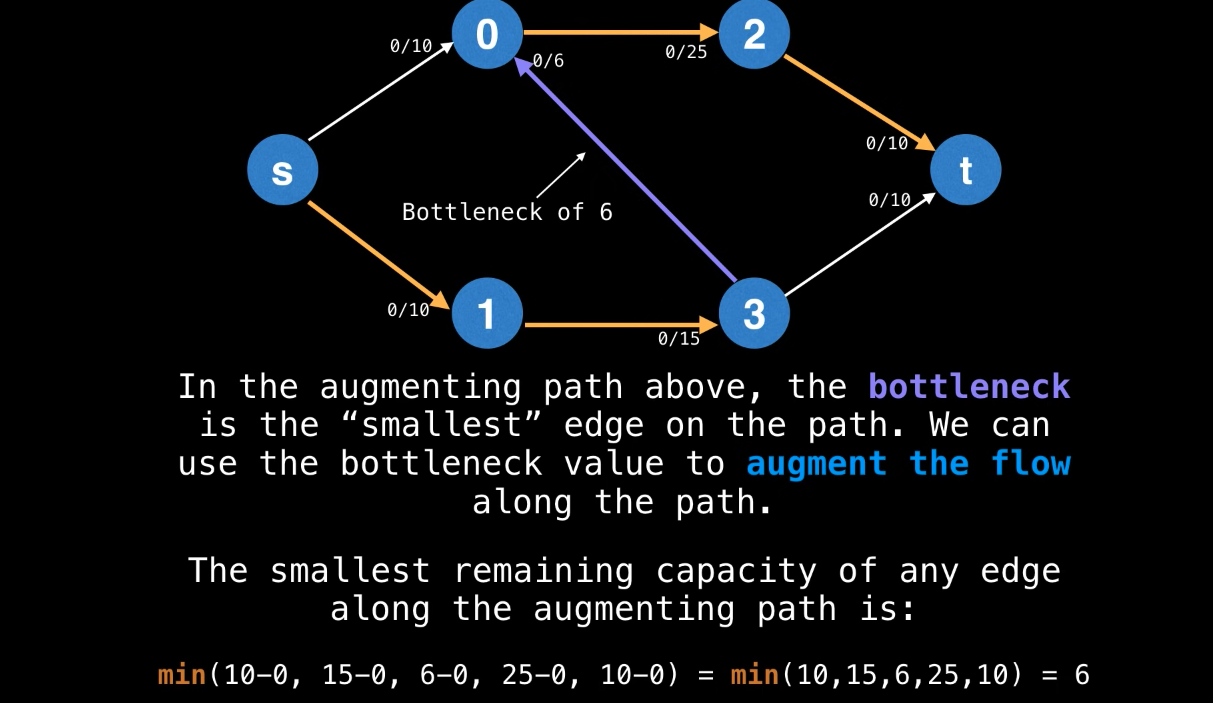
Bottleneck value

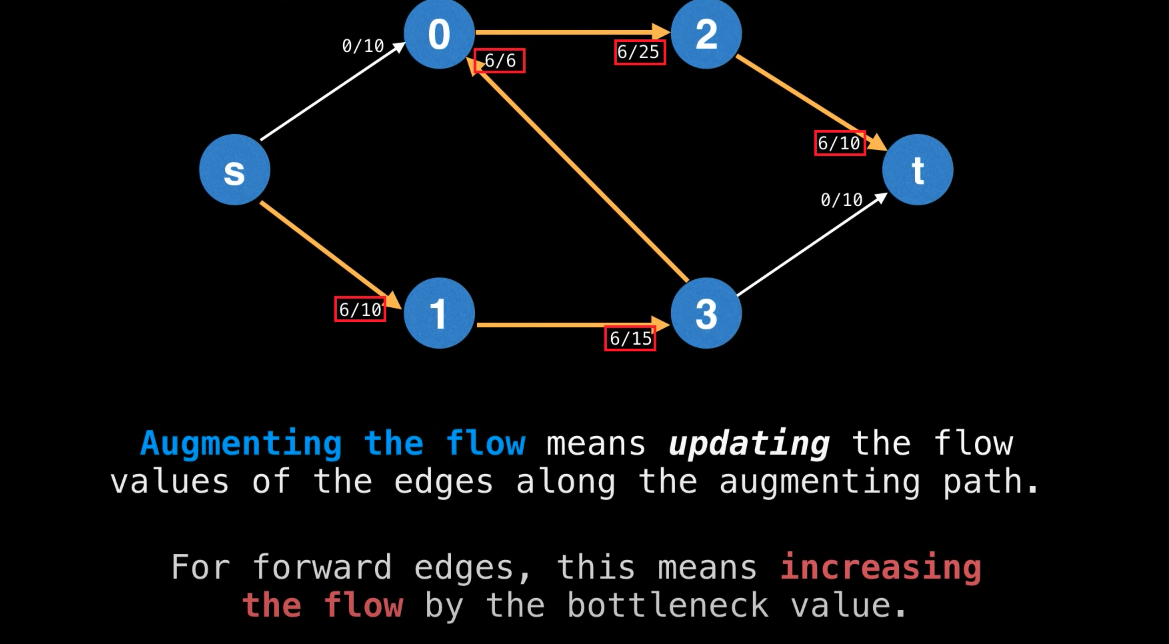
Augmenting the flow value

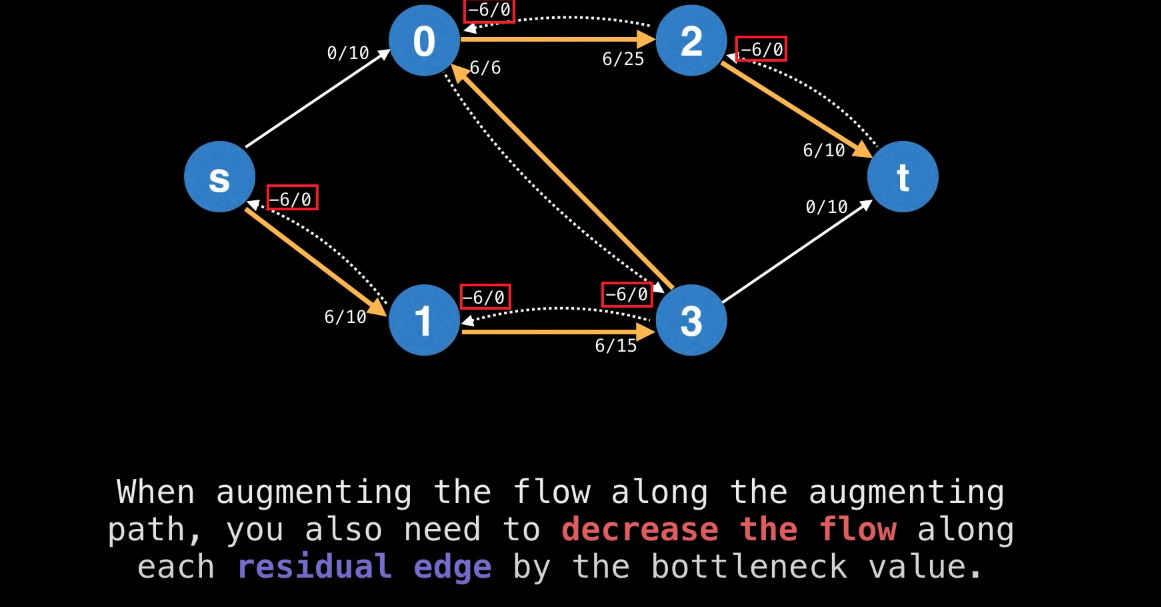
Residual graph

Residual edges exist to "undo" bad augmenting paths which do not lead to a maximum flow

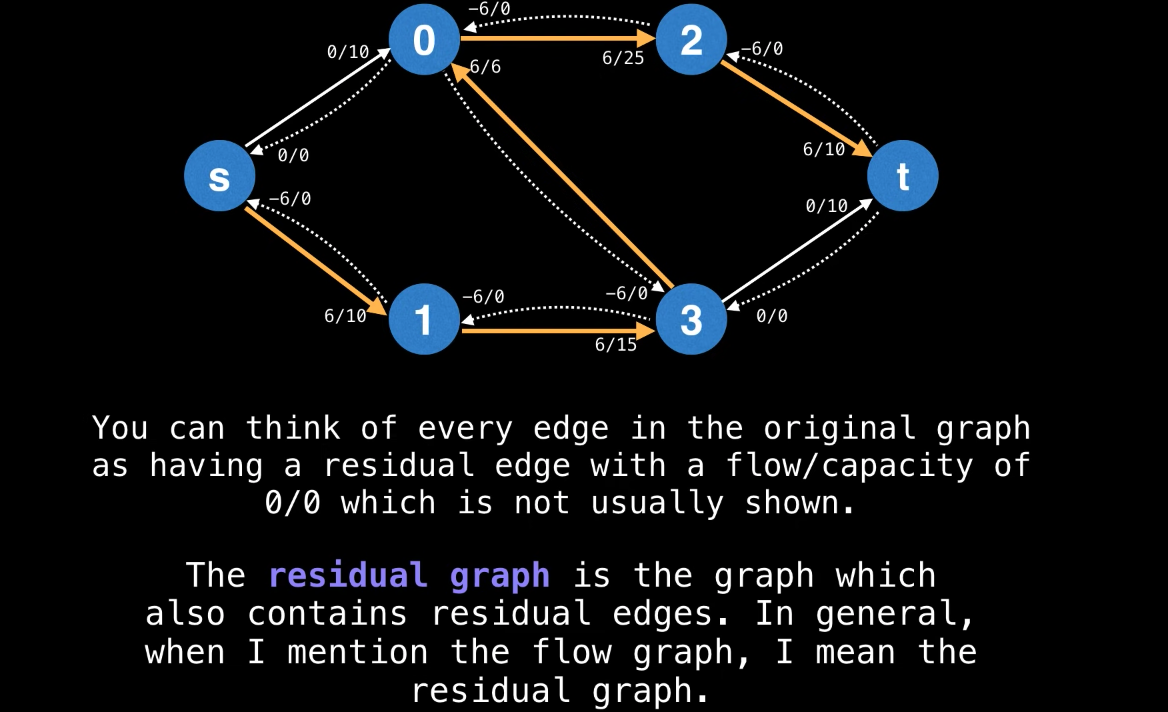
Augmenting paths

1. Let P be an s-t path in the residual graph
2. Let bottleneck(P,f) be the smallest capacity in on any edge of P.
3. If bottleneck(P,f) >0 then we can increase the flow by sending bottleneck(P,f) along the path P.

Pseudocode

Ford-Fulkerson Algorithm

MaxFlow(G):
	// initialize 
	Set f[e] = 0 for all e in G
	
	// while there is an s-t path in Gf
	while P = FindPath(s,t, Residual(G,f)!=None):
		f = augment(f,p)
		UpdateResidual(G,f)
	EndWhile
	Return f

augment(f,P):
	b = bottleneck(P,f)
	For each edge(u,v) in P:
    if e = (u,v) is a forward edge:
      Increase f(e) in G by b  // add some flow
    Else:
      e' = (v,u)
      Decrease f(e') in G by b // erease some flow
    EndIf
   EndFor
   Return f
 

Running time

1. At every step, the flow values are integers。
2. At every step we increase the amount of flow sent by at least 1 unit
3. We can never send more than

Theorem: The Ford-Fulkerson algorithm terminates in C iterations of the while loop.

Time in the while loop

1. If G has m edges, has 2m edges
2. Can find an s-t path in in time O(m+n) time with DFS or BFS
3. Since (every node is adjacent to some edge), O(m+n) = O(m)

Theorem: The Ford-Fulkerson algorithm runs in O(mC) time

Ford-Fulkerson method always terminates if the capacities are integers.

This is because every iteration of Ford-Fulkerson method always finds a new augmenting path and each augmenting path must has bottleneck capacity at least 1 (due to that integer constraint). Therefore, each iteration increases the flow of at least one edge by at least 1, edging the Ford-Fulkerson closer to termination.

As the number of edges is finite (as well as the finite max capacity per edge), this guarantees the eventual termination of Ford-Fulkerson method when the max flow mf is reached and there is no more augmenting path left.

In the worst case, Ford-Fulkerson method runs for mf iterations, and each time it uses O(E) DFS. The rough overall runtime is thus O(mf × E).

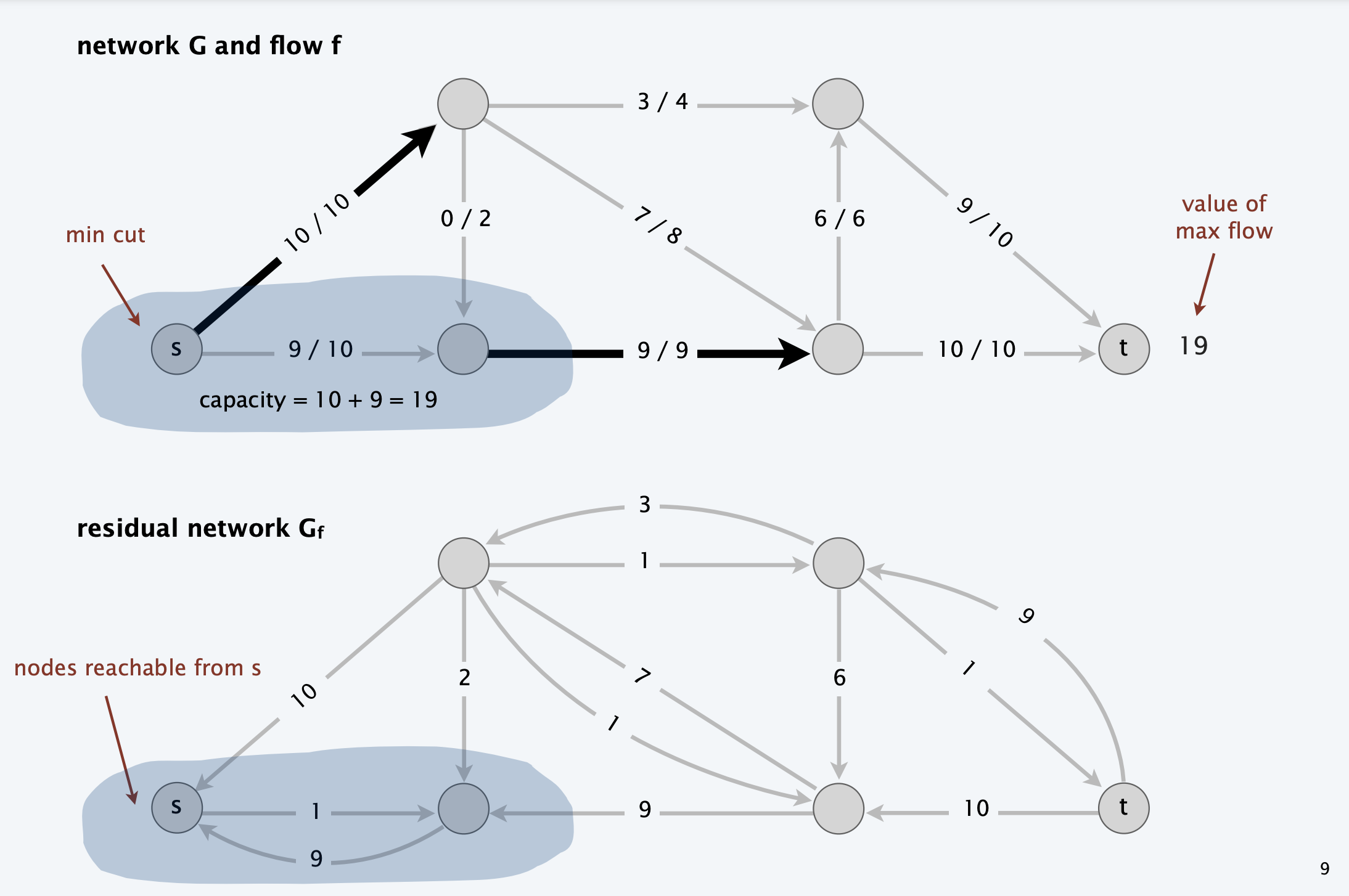
Cuts and Cut capacity

Definition: The capacity(A,B) of an s-t cut (A,B) is the sum of the capacities of edges leaving A.

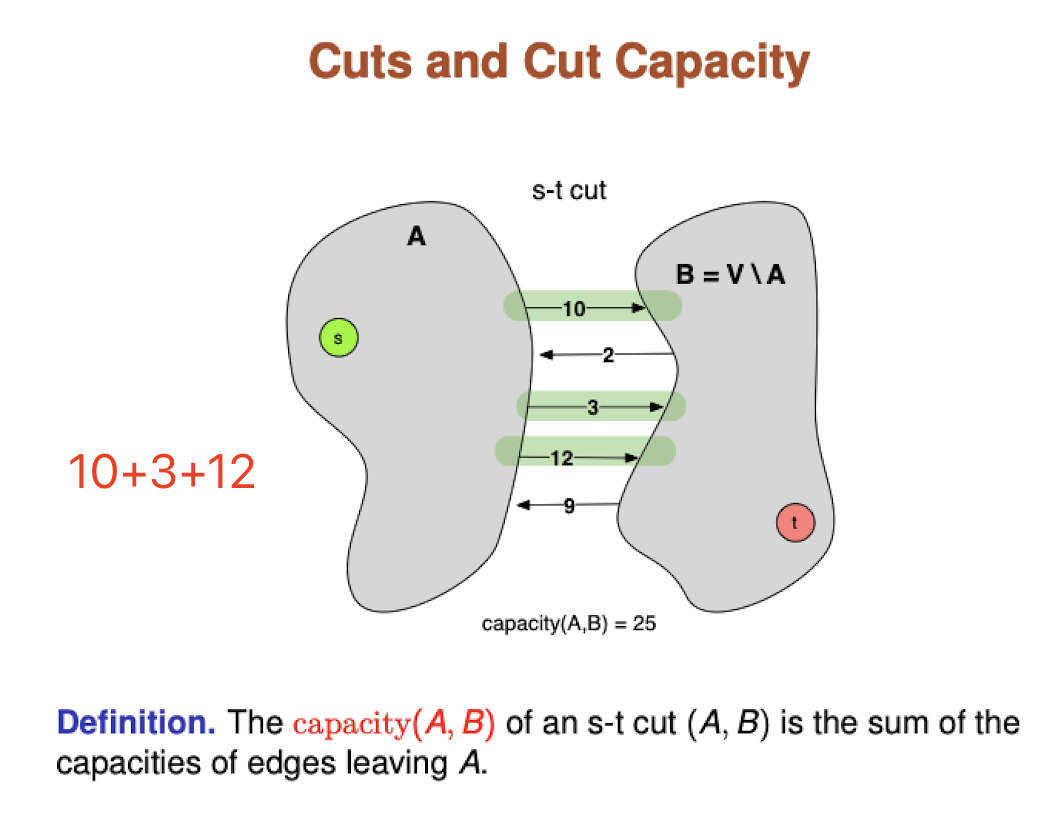
Theorem: Let f be an s-t flow and (A,B) be an s-t cut. Then v(f) =

Cuts constraint flows

Theorem:

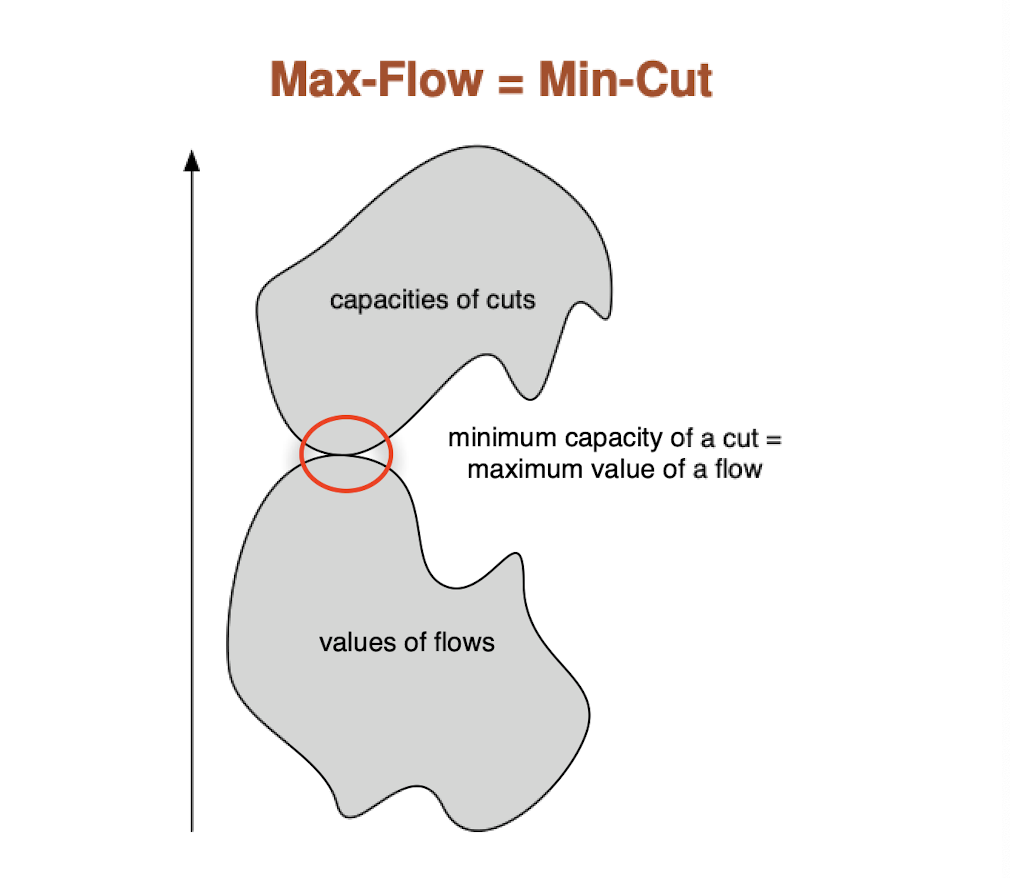
Max-Flow = Min-Cut

This famous theorem states that in a flow network, the maximum flow from s to t is equal to the total weight of the edges in a minimum cut, i.e., the smallest total weight of the edges that have to be removed to disconnect s from t.

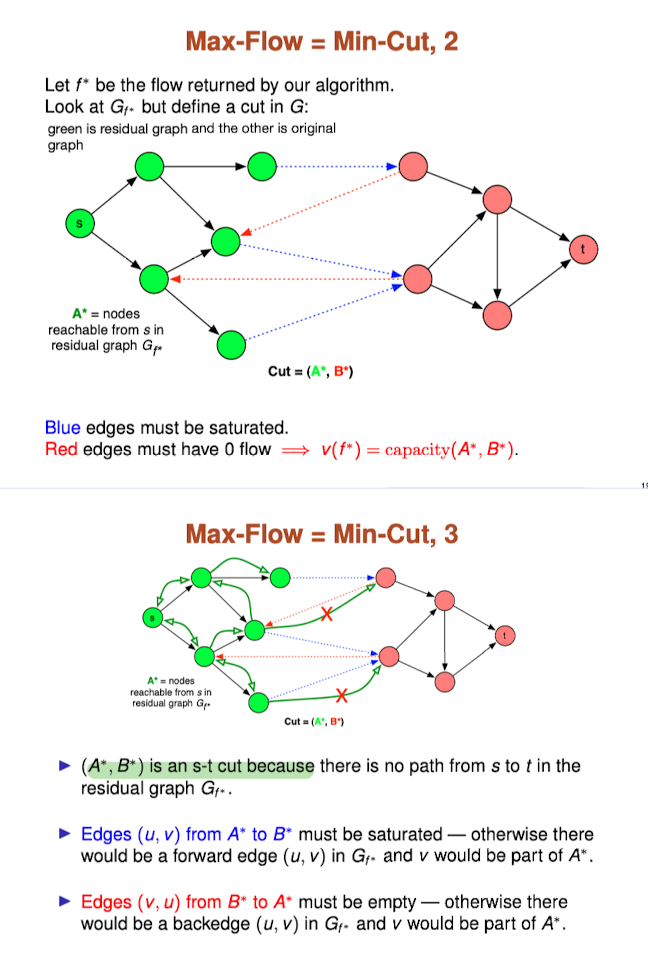
Finding the min-capacity cut

Our proof that maximum flow = minimum cut can be used to actually find the minimum capacity cut:

1. Find the maximum flow f*
2. Construct the residual graph for
3. Do a BFS to find the nodes reachable from s in . Let the set of these nodes be called
4. Let be all other nodes
5. Return () as the minimum capacity cut.

Summary of maximum flow problem

1. Ford-Fulkerson algorithm can find max flow in time
2. Send flow among some path with capacity left, possibly by “erasing “ some flow we’ve already sent.
   • Use residual graph to keep track of remaining capacities and flow we’ve already sent
   • Argument paths
3. All cuts have capacity the value of all flows
4. Now the flow is maximum because its value equals the capacity of some cut.

Bipartite graphs

1. Suppose we have a set of people and set of jobs R
2. Each person can do only some of the jobs
3. Can model this as a bipartite graph

Bipartite matching

1. A matching gives an assignment of people to tasks
2. Want to get as many tasks done as possible
3. Want a maximum matching: one that contains as many as edges possible

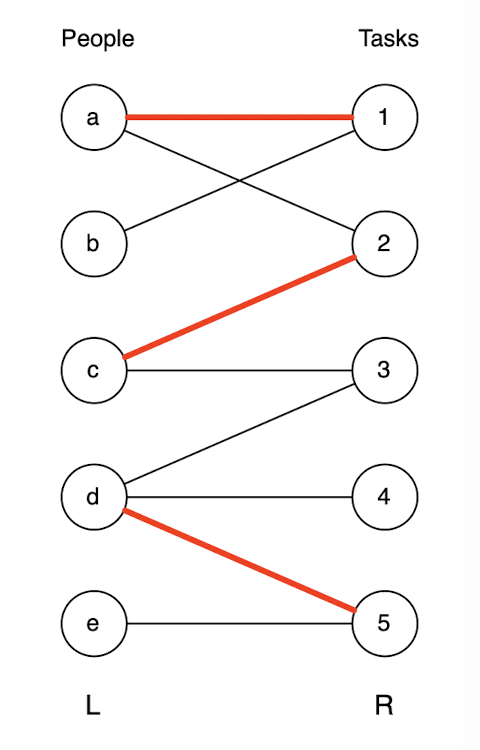
Maximum Bipartite Matching

Problem: Given a bipartite graph , find an that is a matching and is large as possible

• We’re given A and B so we don’t have to find them
• S is a perfect matching if every vertex is matched
• Maximum Maximal

Maximum (multiple): some matching, you cannot obtain by adding into the network

Maximal: cannot be improved

Reduce

1. Given an instance of bipartite matching
2. Create an instance of network flow
3. Where the solution to the network flow problem can easily be used to find the solution to bipartite matching.

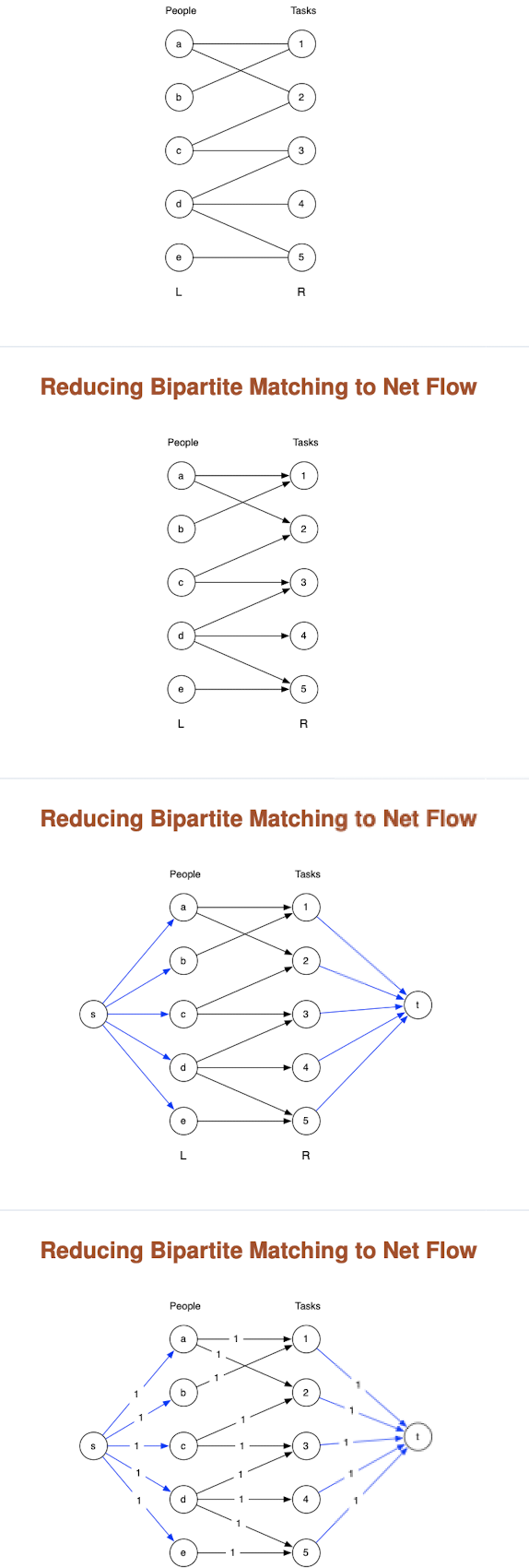
Use network flow to solve Bipartite Matching

Recap:

1. Given bipartite graph , direct the edges from A to B
2. Add new vectors s and t
3. Add an edge from s to every vertex in A
4. Add an edge from every vertex in B to t.
5. Make all the capacities 1.
6. Solve maximum network flow problem on this new graph

The edges used in the maximum network flow will correspond to the largest possible matching!

Analysis

• Because the capacities are integers, our flow will be integral
• Because the capacities are all 1, we will either:
  • Use an edge completely (sending 1 unit of flow) or
  • Not use an edge at all
• Let M be the set of edges going from A to be that we use
• We need to prove that
  • M is a matching
  • M is the largest possible matching

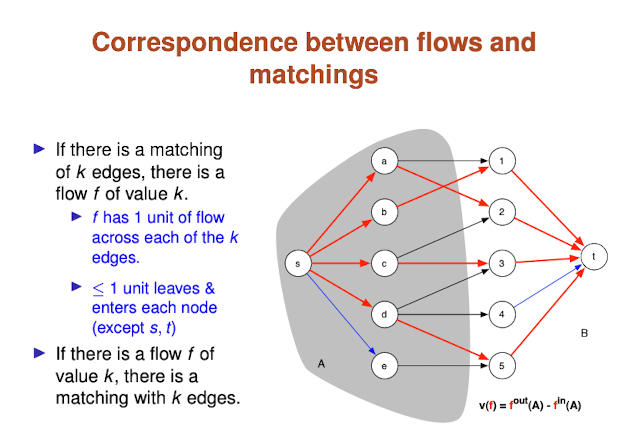
M is a matching

1. We can choose at most one edge leaving any node in A
2. We can choose at most one edge entering any node in B

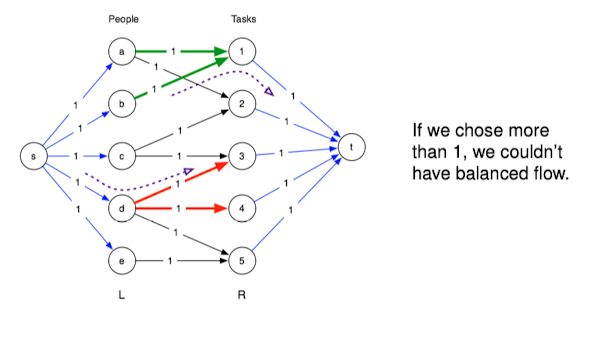
M is as large as possible

1. We find the maximum flow (say with k edges)
2. This corresponds to a matching M of k edges
3. If there were a matching with > k edges, we would have found a flow with value > k, contradicting that f was maximum
4. Hence, M is maximum

Run time

Summary of the Bipartite graphs

Image segmentation

• Given an image, what is foreground and what is the background?
• If (x,y) is a foreground pixel, then nearby pixels are also likely foreground

Abstract rules:

1. = likelihood that pixel is in foreground
2. = likelihood that pixel is in background
3. = the penalty for putting one of i,j in foreground and the other sun the background

We add new parameters to model separating neighboring pixels. For every neighboring pair of pixels {i, j}, we have a parameter

Clumping

All else equal, if , then we should make a foreground pixel

But: we noted that foreground pixels tend to be near one another, and background pixels tend to be near one another.

Image segmentation problem

Partition the set of pixels into two sets A and B to maximize:

Min-cut

Image segmentation:

Partition the vertices of the image graph into 2 sets A,B to maximize q(A,B).

Minimum Cut:

Partition the vertices of a directed graph into 2 sets A, B with to minimize weight of edges crossing A to B

Difference comparison

• Maximization vs. Minimization
• Image segmentation has no source or sink
• Image segmentation has a more complicated objective function q(A,B) with weights on the nodes
• Undirected vs directed

Reduction

Add source and sink

We would add:

1. A source with an edge (s,u) for every vertex u.
2. A sink t with an edge (u,t) for every vertex u.

We will see: s will represent the foreground, and t will represent the background

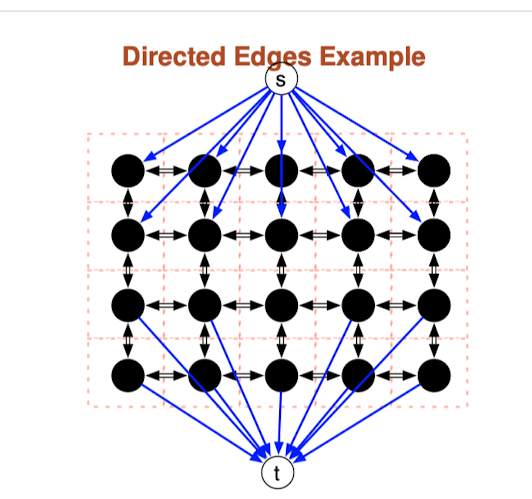
Directed edges

We convert the currently undirected graph into a directed graph

• Edges adjacent to s are directed so they leave s
• Edges adjacent to t are directed so they enter t
• All other edges are replaced by 2, anti-parallel edges

Summary of previous work

Maximization vs. Minimization

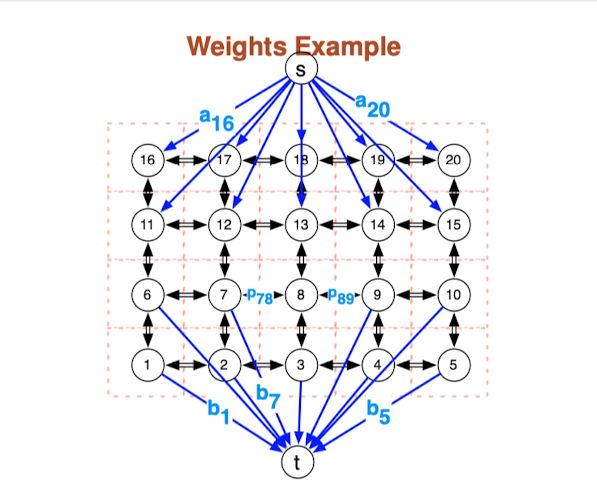
Parameters used in this image segmentation problem

• Edges between two pixels and get weight
• Edge (s,i) gets weight
• Edge (j,t) gets weight

The intuition here is the capacity of s-t cut (A,B) will equal the quantity we are trying to minimize

Therefore, if we find the min cut, we will find the best partition into foreground and background

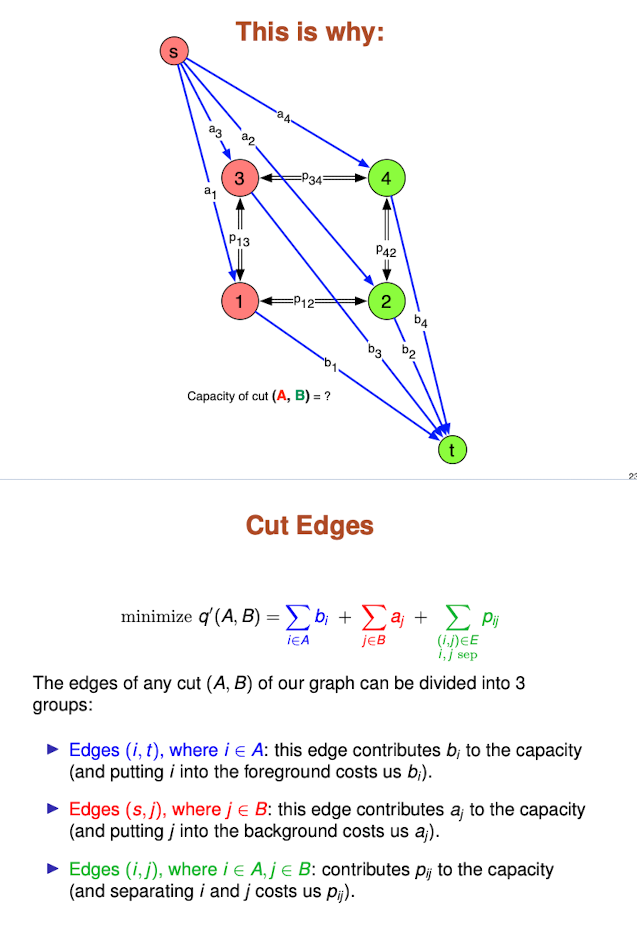
Capacity of a cut = quality of partition

The capacity of an s-t cut (A,B) equals the quality of the partition defined by taking:

1. A to be the set of foreground pixels (plus s)
2. B to be the set of background pixels (plus t)

Summary

Circulations with Demands

1. Suppose we have multiple sources and multiple sinks
2. Each sink wants to get a certain amount of flow (its demand)
3. Each source has a certain amount of flow to give (its supply)
4. We can represent supply as negative demand

Sources and sinks

Let S be the set of nodes with negative demands (supply)

Let T be the set of nodes with positive demands (demand)

In order for there to be a feasible flow, we must have:

Reduction to circulation with demands

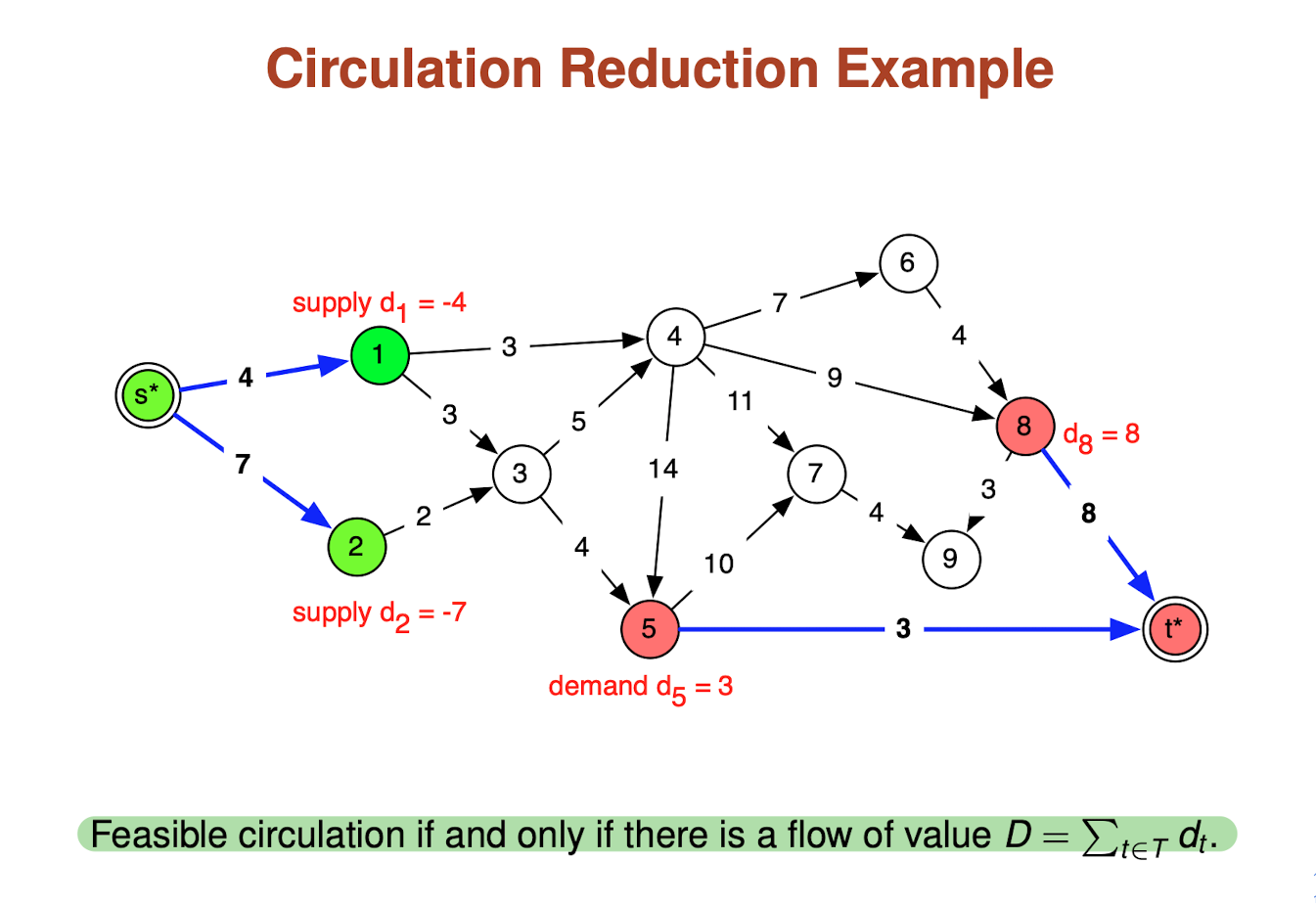
Notes

• Capacity of edges (s*, s) limit the supply for source nodes s
• Capacity of edges (t, t*) require that flow reaches each t

Hence, we could use max-flow method to find these circulations

Lower Bounds

What if we want lower bounds on what flow goes through some edges?

We want to require that some edges are used

Goal: find a flow f that satisfies:

1. Capacity constraints: For each
2. Demand constraints: For each ,

Suppose we defined an initial flow by setting the flow along each edge equal to the lower bound. In other words . This flow satisfies the capacity constraints, but not the demand constraints

New graph

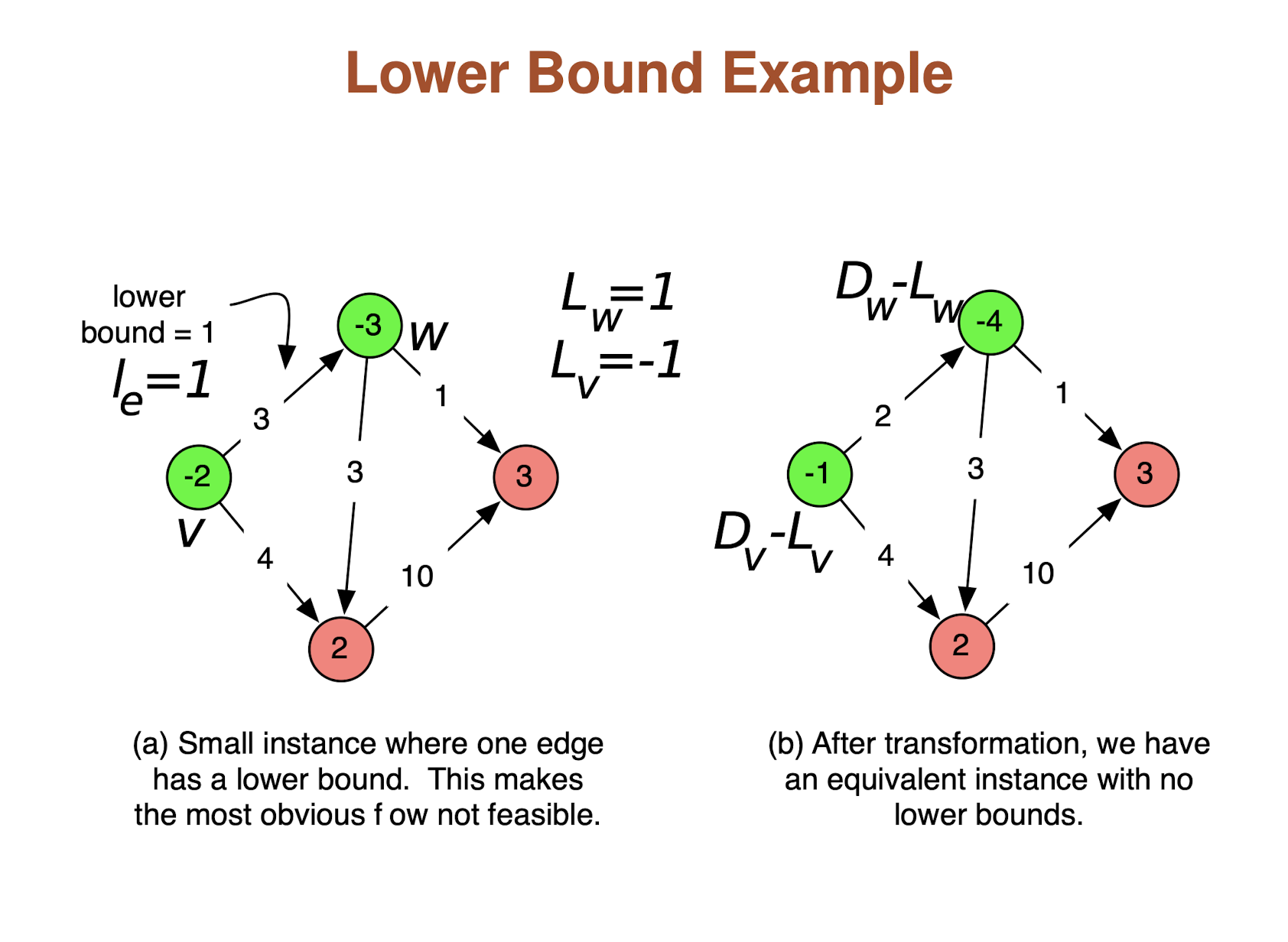
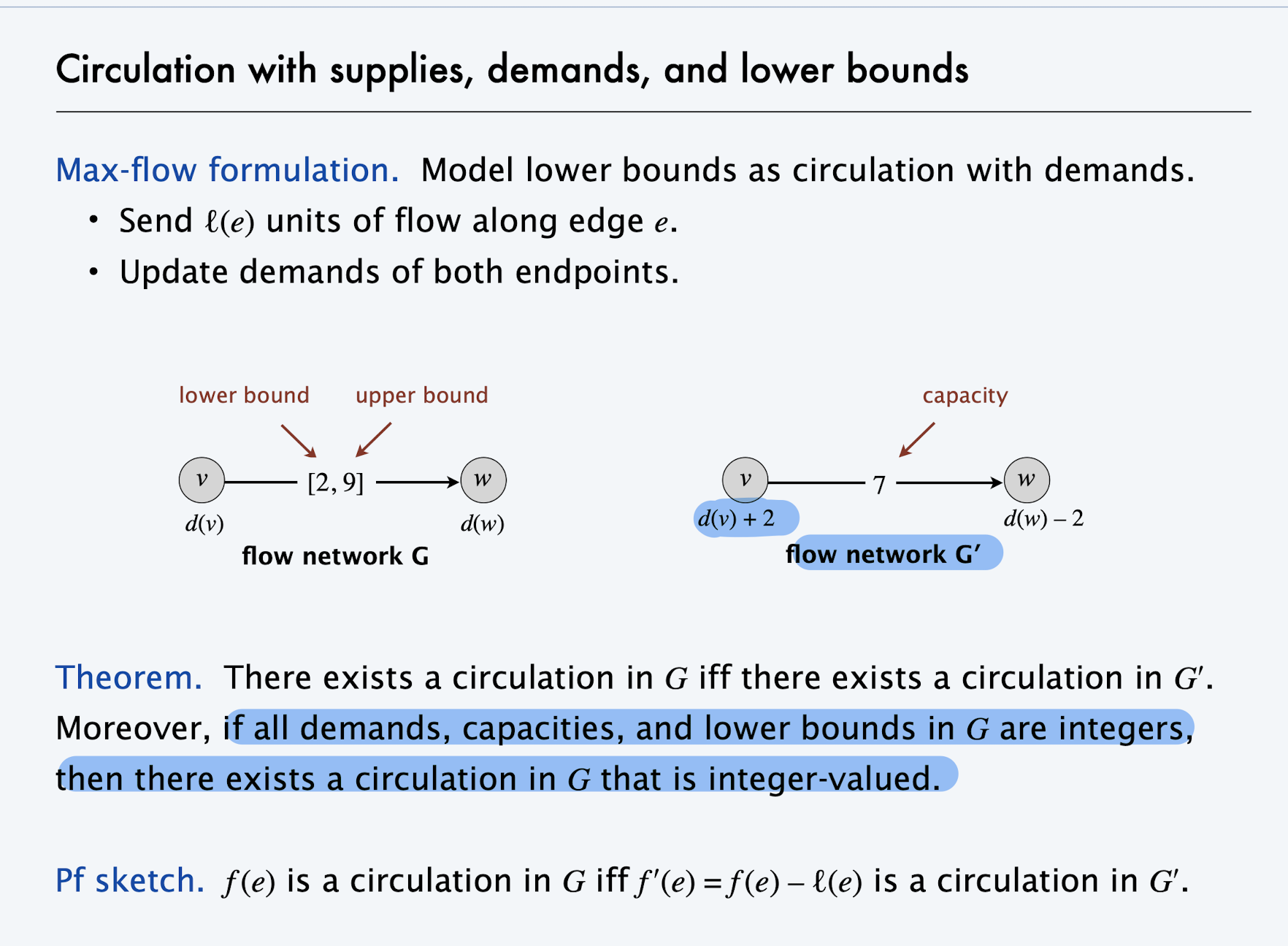
Homework problems

Magic binary square

https://stackoverflow.com/questions/56366068/check-if-it-is-possible-to-create-a-binary-matrix-when-sum-of-each-row-and-colum