splay trees and BST algo notes

BST definition

Property: if a node has key k then keys in the left subtree are < k and keys in the right subtree are > k. For convenience, we disallow the duplicate keys.

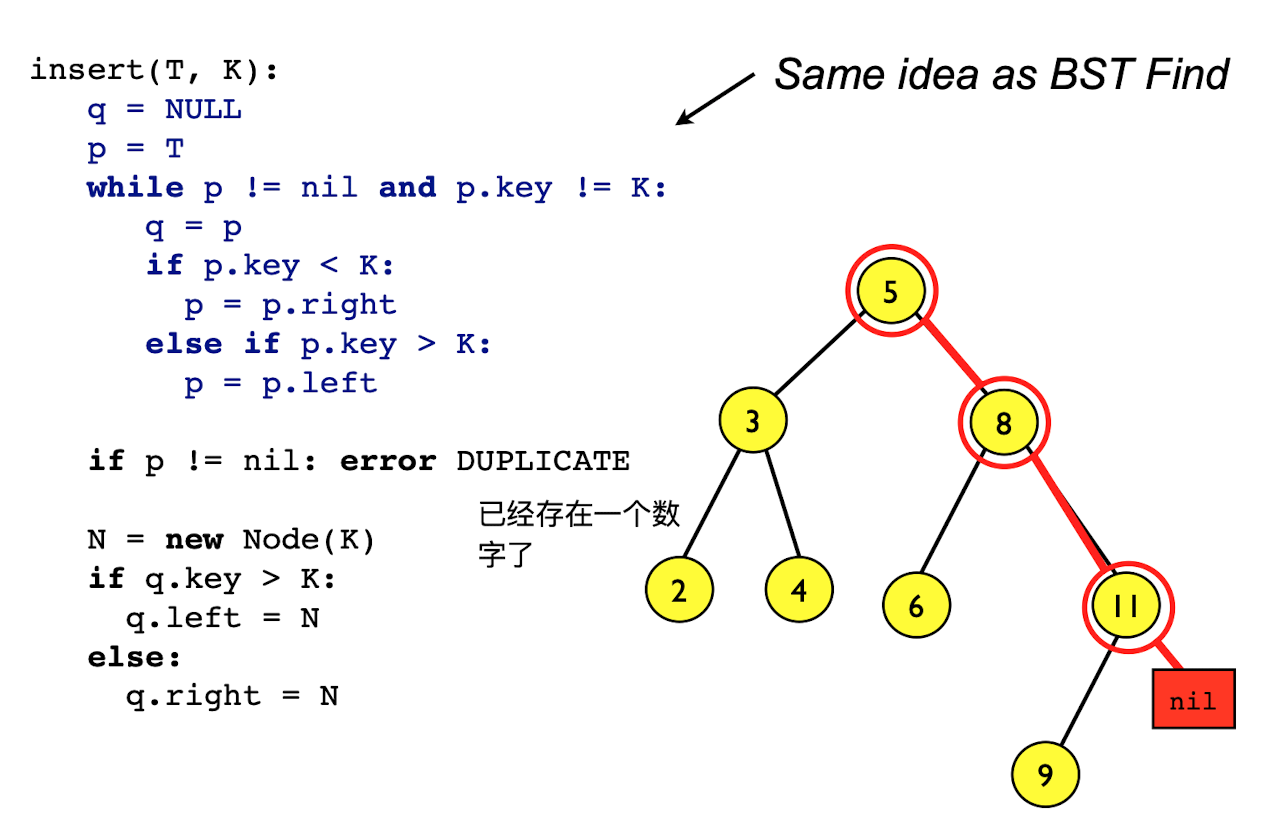
Find & Insert

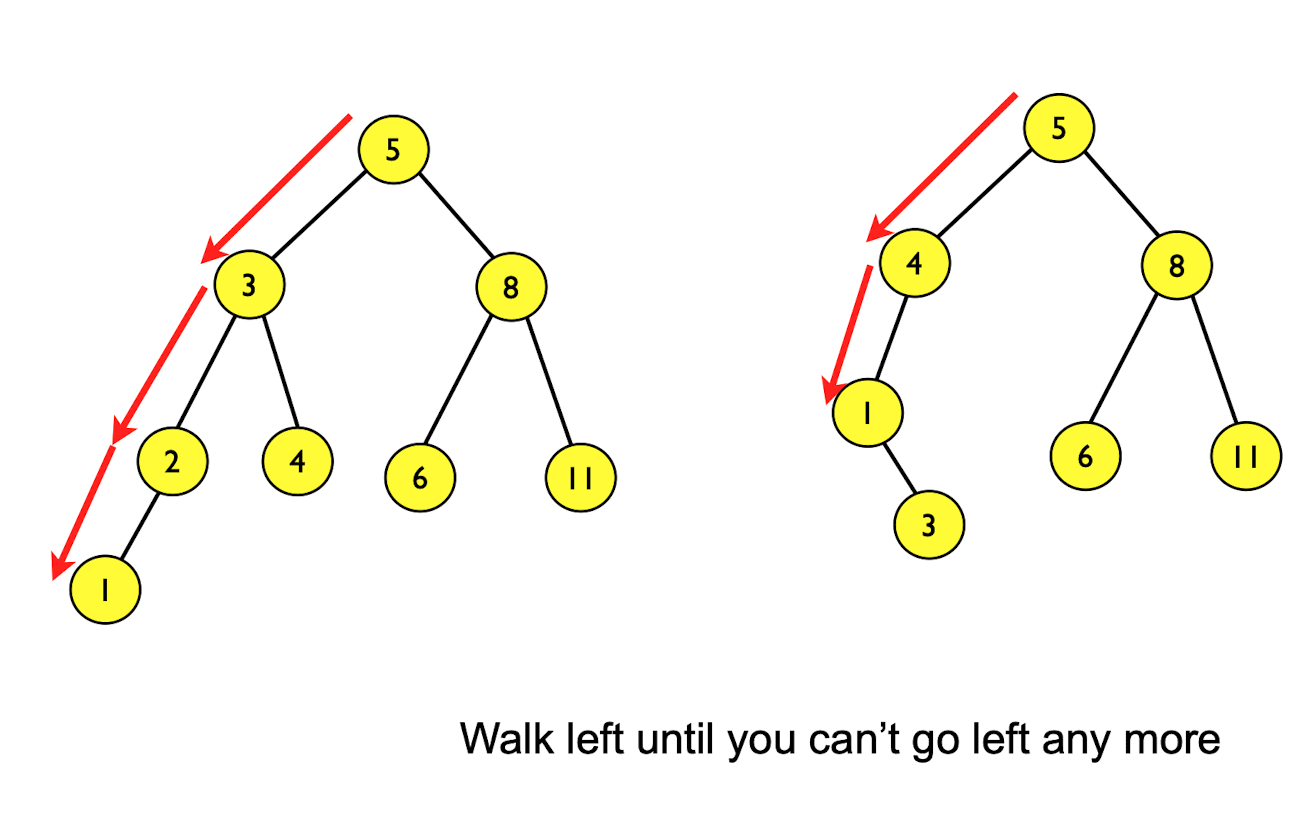
FindMin

Walk left until you can’t go left any more

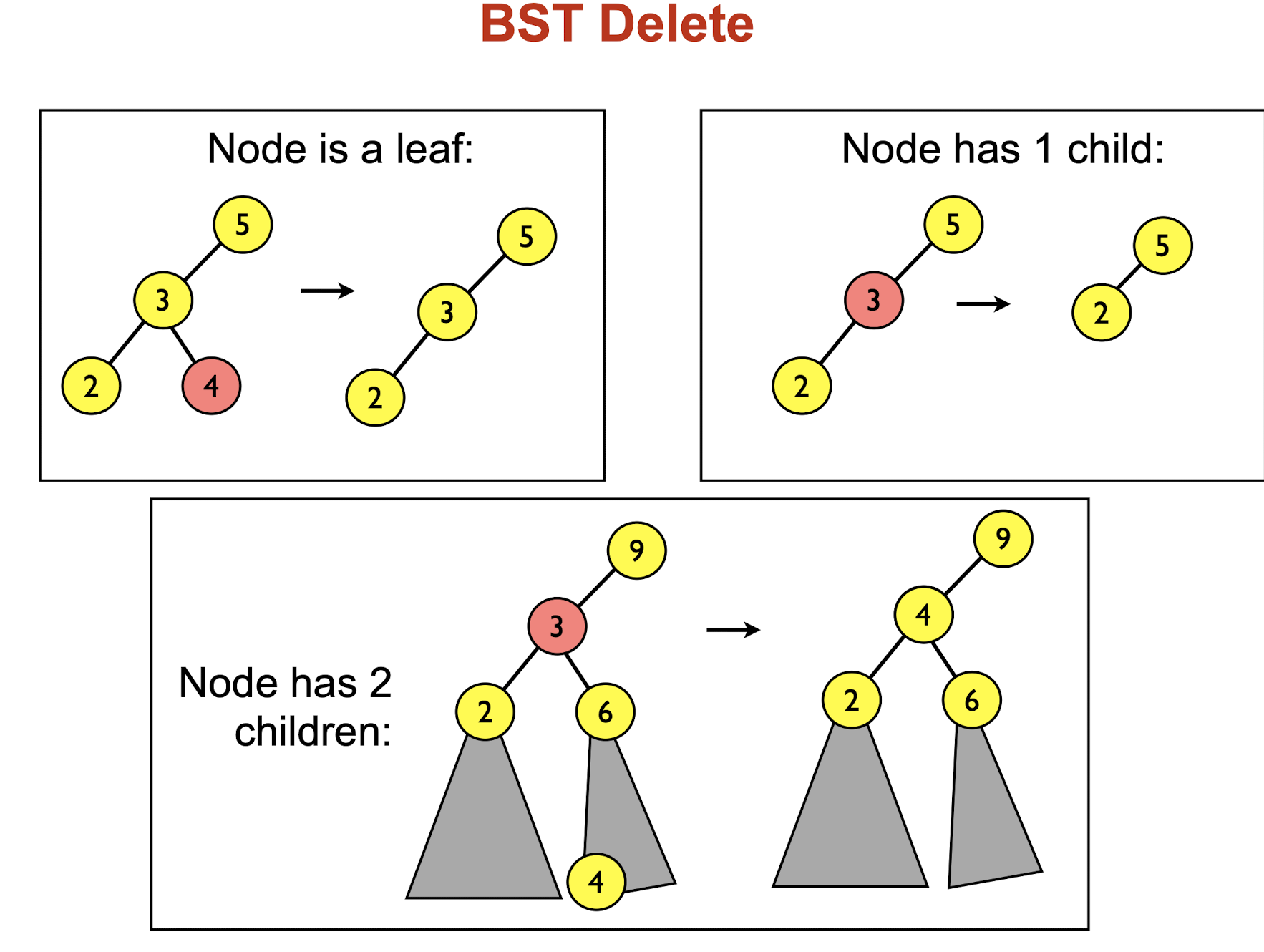
Delete

BST Operations summary

Find

Walk left or right according to the key comparison

Insert

Put the new node where a Find for it would have fallen off the tree

Delete

1. If deleting a leaf, just remove it
2. If deleting a node u with 1 child, move that child up to be a child of u’s parent
3. If deleting a node u with 2 children: find the smallest key in the right subtree rooted at u, delete it, and replace u with that key

Analysis

What’s the worst possible insertion order

Insertion should start from the root of the tree, to the low maximum length. Order matters.

Insert keys in increasing trees and continue to add in increasing order (e.g. continue to add to the right of the BST)

Same to the structure of the Linked list, and the insertion, deletion and find would be O(N)

What’s the best possible insertion order

The depth of left subtrees and right subtrees are roughly the same would be the best. Also, called as the balanced tree

• Need a method to force a BST tree to be balanced if items are constantly being inserted and deleted.
• Splay trees are thus proposed

BST Java implementation

https://yuxuanwu17.github.io/2021/07/26/2021-07-26-%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE%E6%A0%91%EF%BC%88Binary-Search-Tree%EF%BC%89/

Splay trees

Characters

1. No extra storage requirement
2. Simple to implement
3. Main idea: move frequently accessed items up in tree
4. Amortized O(log n) performance
5. Worst case single operation is

Operations

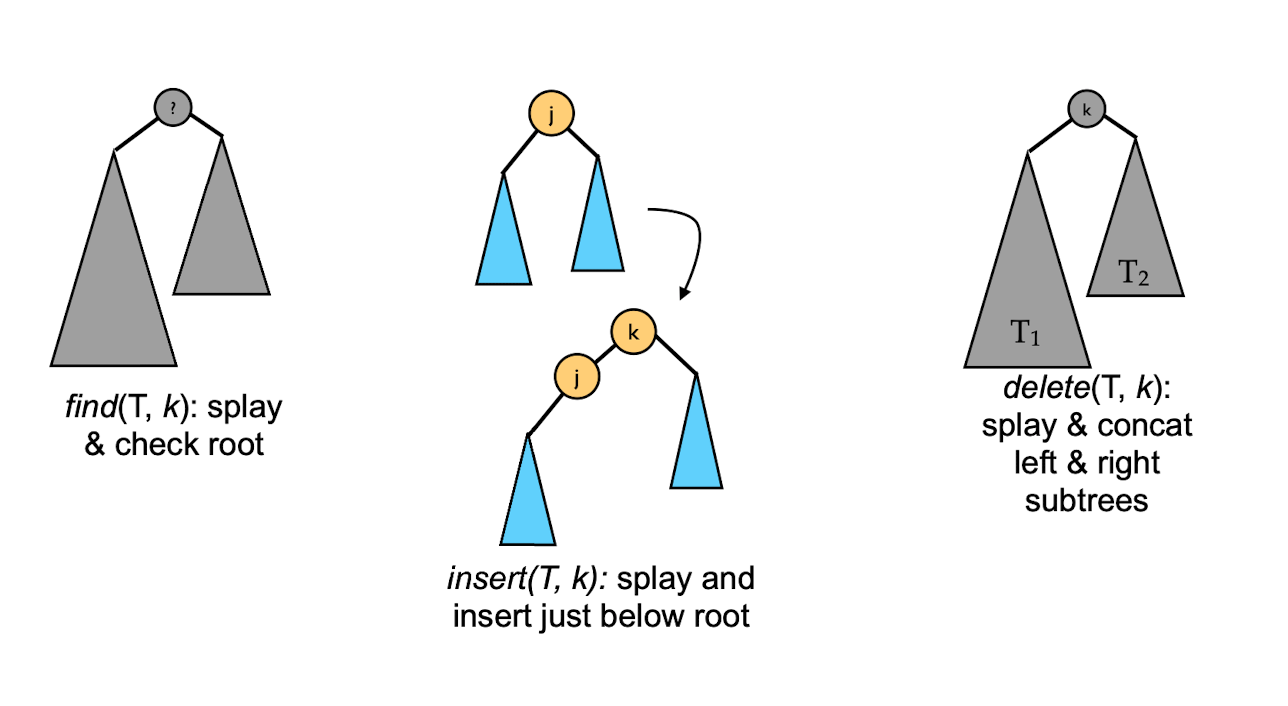
Splay (T, K): if k T, then move k to the root using a particular set of transformations of the tree. Otherwise, move either inorder successor or predecessor of k to the root

find(T,k): splay(T,k). If root(T) = k, return k, otherwise return not found.

insert(T,k): splay(T,k). If root(T) = k, return duplicate! Otherwise, make k the root and add children as in figure

concat(T1,T2): Assumes all keys in T1 are < all keys in T2. Splay(T1, infinity). Now root T1 contains the largest item and has no right child. Make T2 right child of T1

delete(T,k): splay(T,k). If root r contains k, concat(Left(r),Right(r))

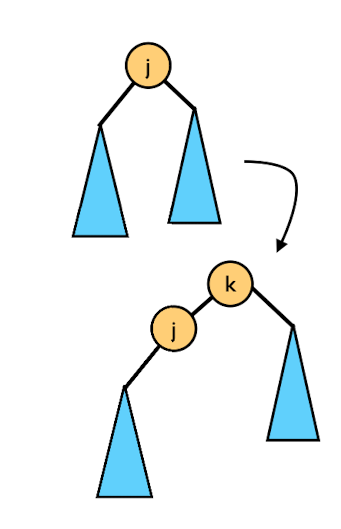
The rotation would not change the in-order traversal.

Find operation

1. Like a standard BST search operation
2. We make rotations when we find the given element we are looking for -> it is going to be the root node, which also called as “splaying” (It don’t need to be strictly balanced)
3. Why? Because in the next search it can be accessed very fast even in O(1) time
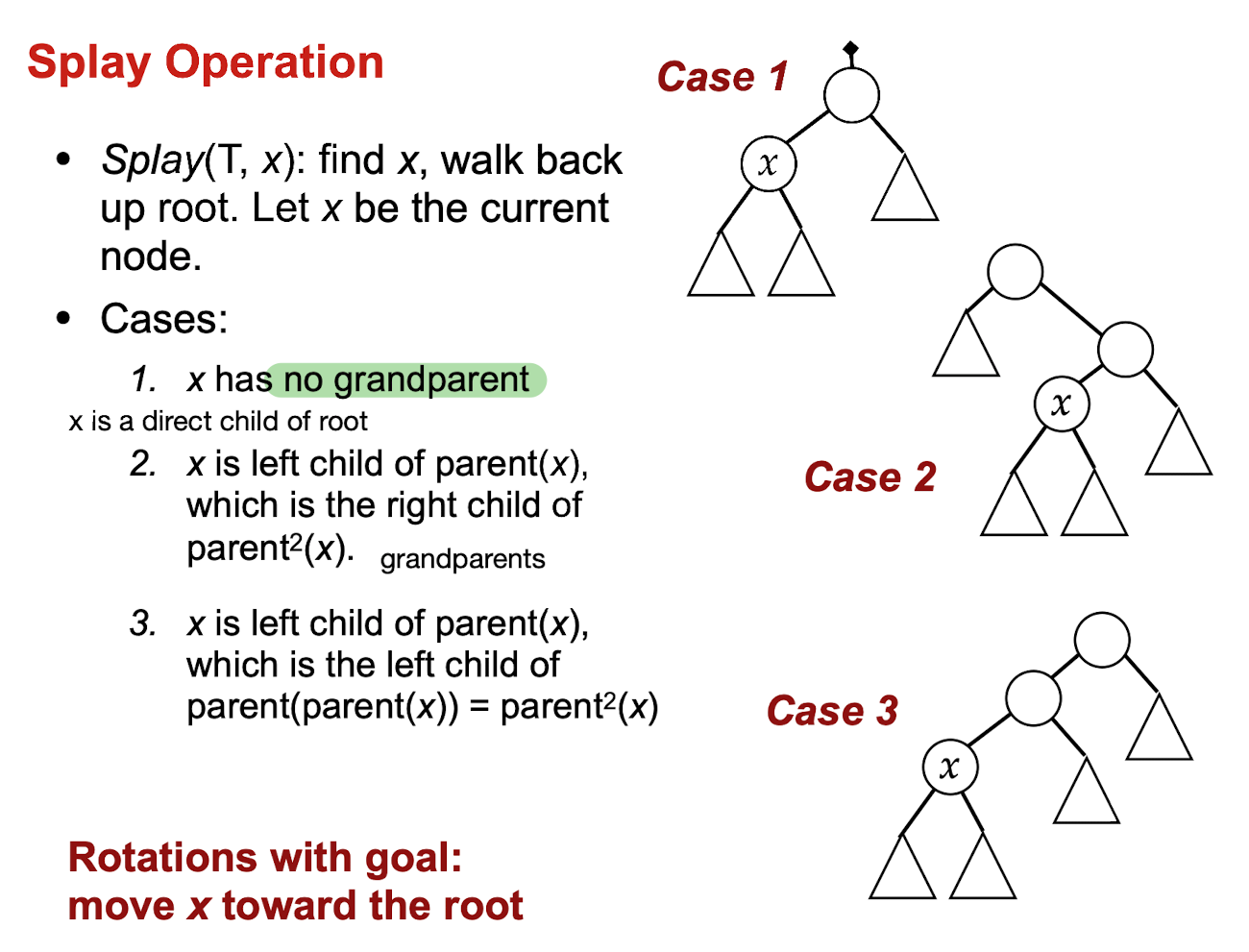
4. There are 3 ways we can make it happen
   1. Zig-zag situation
   2. Zig-zig situation
   3. Zig situation

The priority was not to be balance, but to find the root we are looking for

Zig-zag situation (two rotations)

• The given node X is a right child of a left child
• The given node X is a left child of a right child

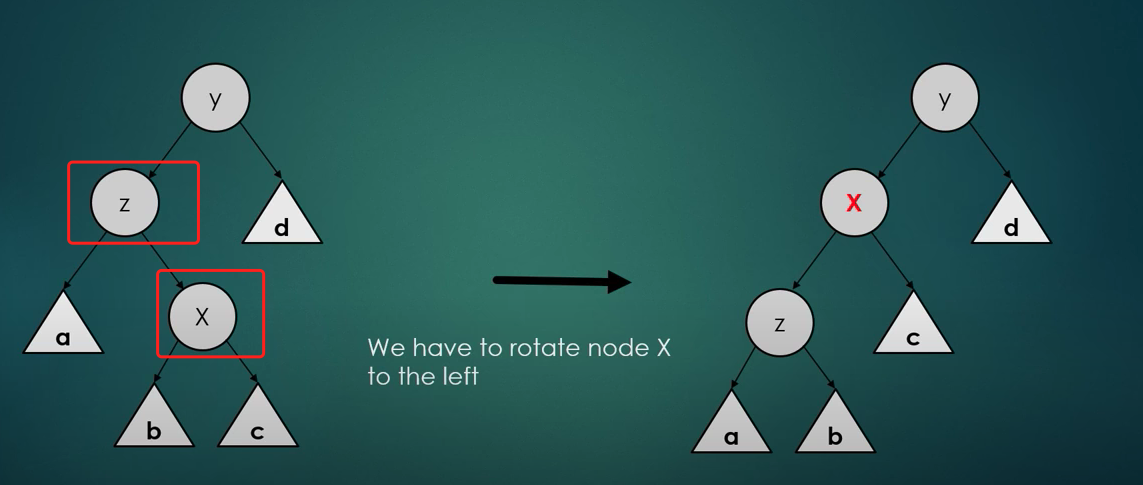
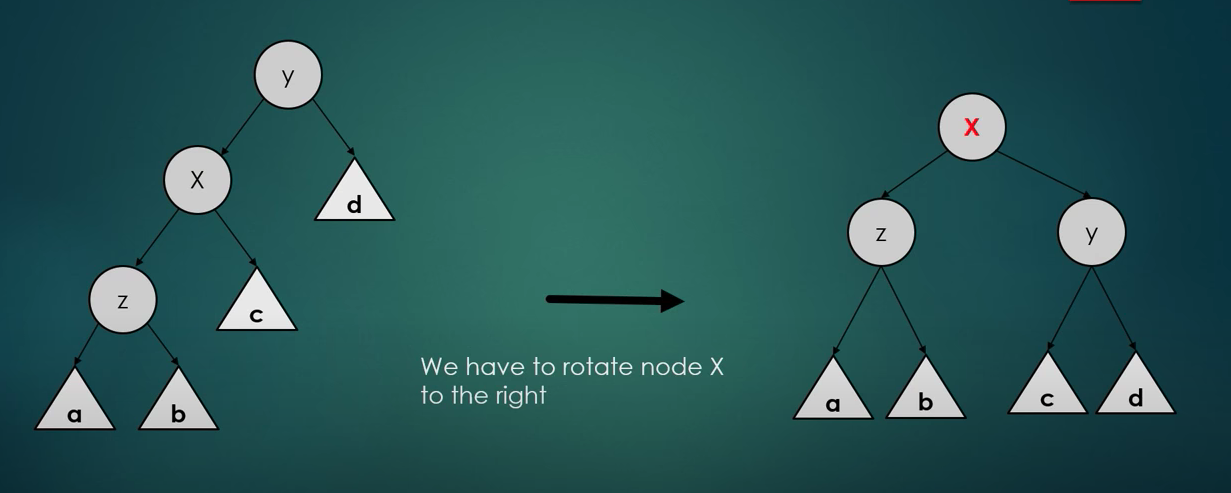
Zig-zig situation (Two rotations)

• The given node X is left child of a left child
• The given node X is a right child of a right child

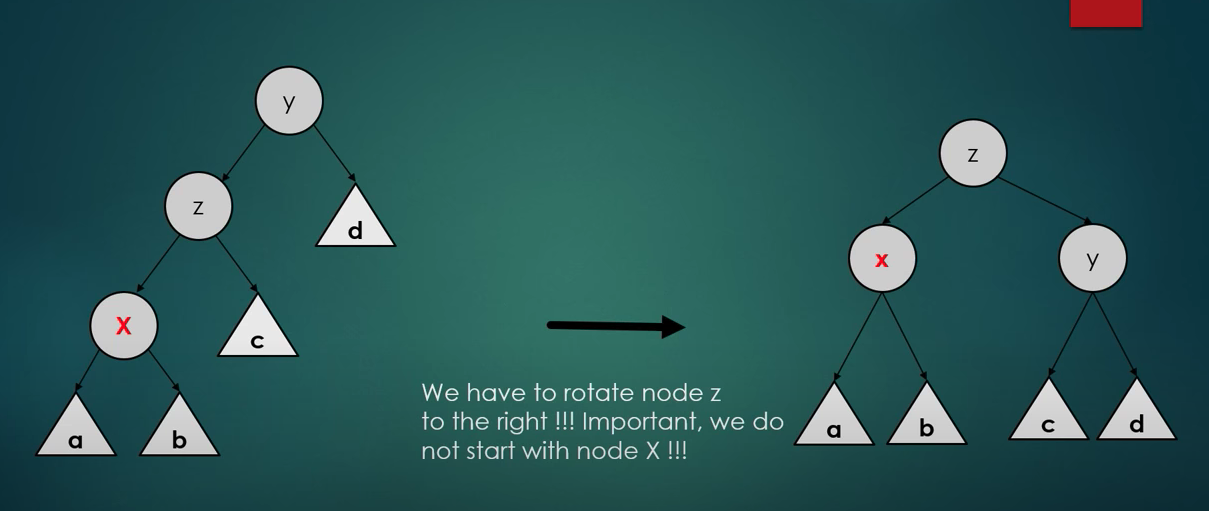
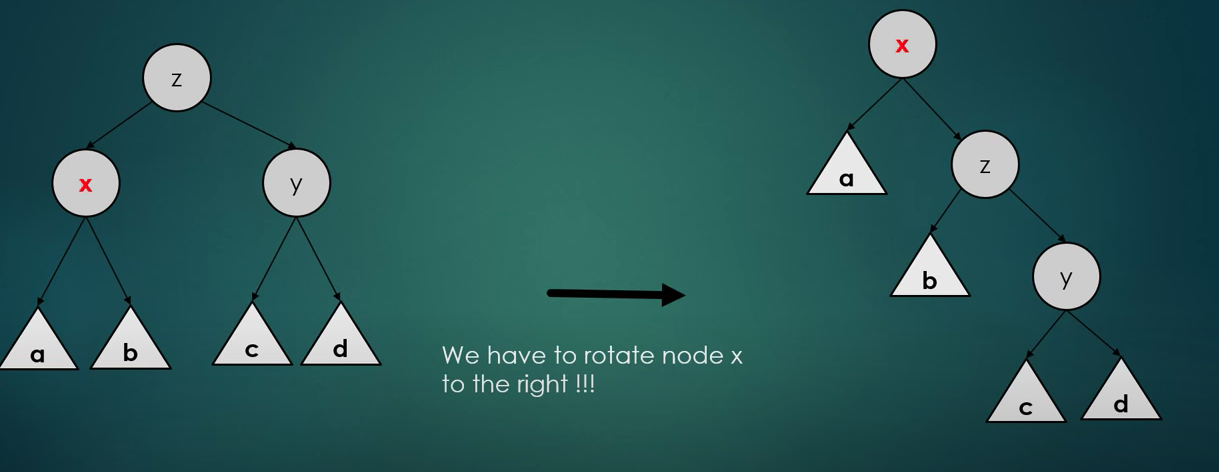
Zig situation (single rotation)

• We have to repeat the previous two steps over and over again until we get to the root
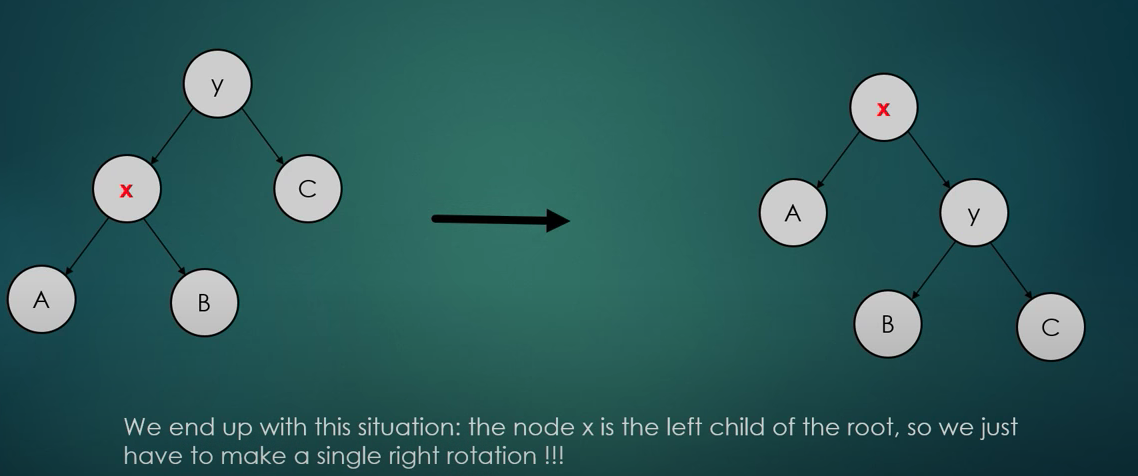
• Sometimes we end up at the left/right child of the root: we just have to make a single right/left rotation accordingly
• So here X is just the child of the root

Summary

Time complexity:

• Self adjusting binary search trees
• Guarantee that any m consecutive tree operations starting from an empty tree take O(m log n) time, where n is the maximum number of elements in tree at any time
• Another way of saying this is that the average cost of an operation (averaged over all the operations) is O(log n). Note: this makes no assumption about the sequence of accesses
• Call this amortized logarithmic cost

Find => Rotation => insertion

Splay idea

• The find/insert/delete operations can be written in terms of the “splay operation”
• Splay is implemented by doing a standard BST “find” and then applying particular rotations walking back up toward the root
• Splay may actually make the tree worse, but over a series of operations the tree always gets better (a slow find results in a long splay, but this long splay tends to flatten the tree a lot)