b trees algo notes

2，3 Trees

1. All levels are at the same level
2. Each internal node has either 2 or 3 children
3. If it has:
   1. 2 children => it has 1 key
   2. 3 children => it has 2 keys

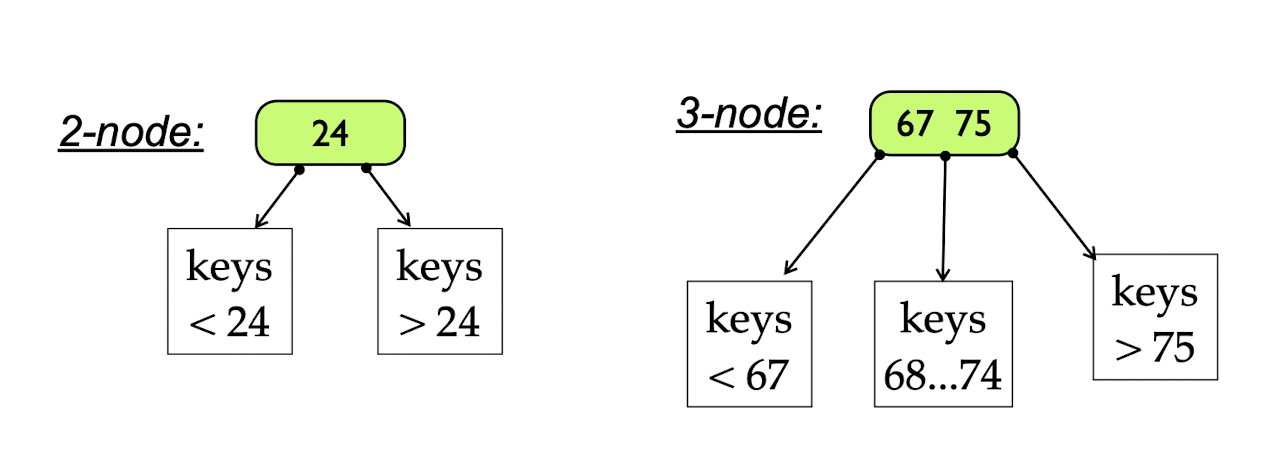
Find operation (multiway searching)

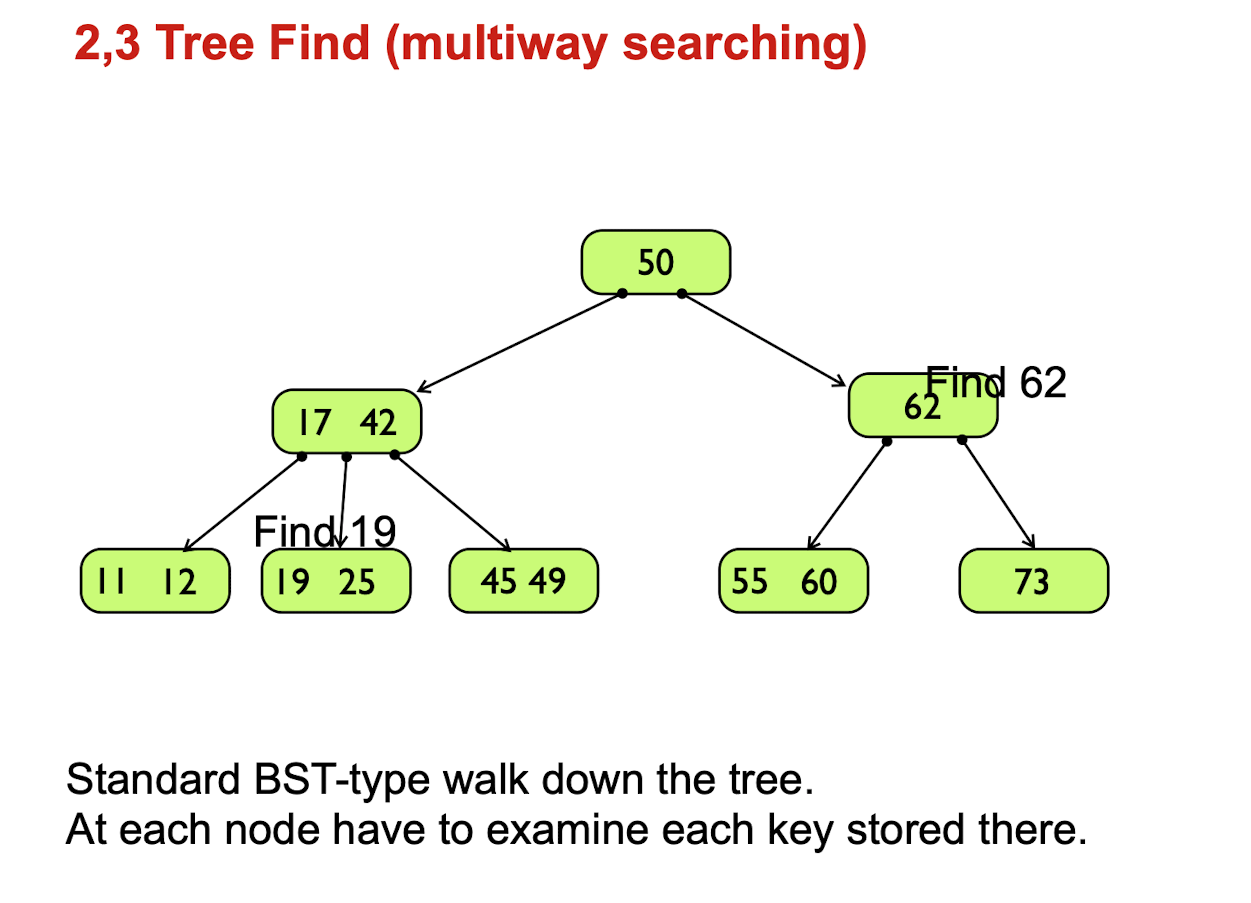
Insert operation

Condition 1

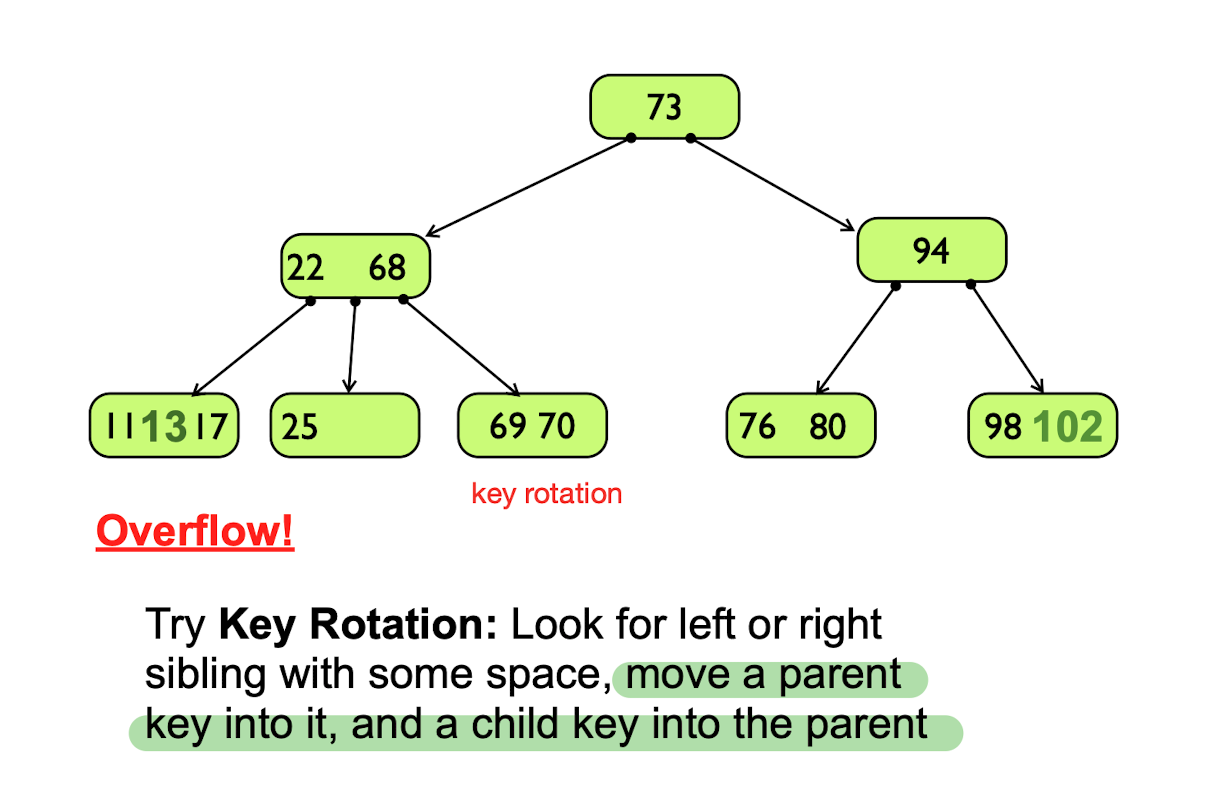
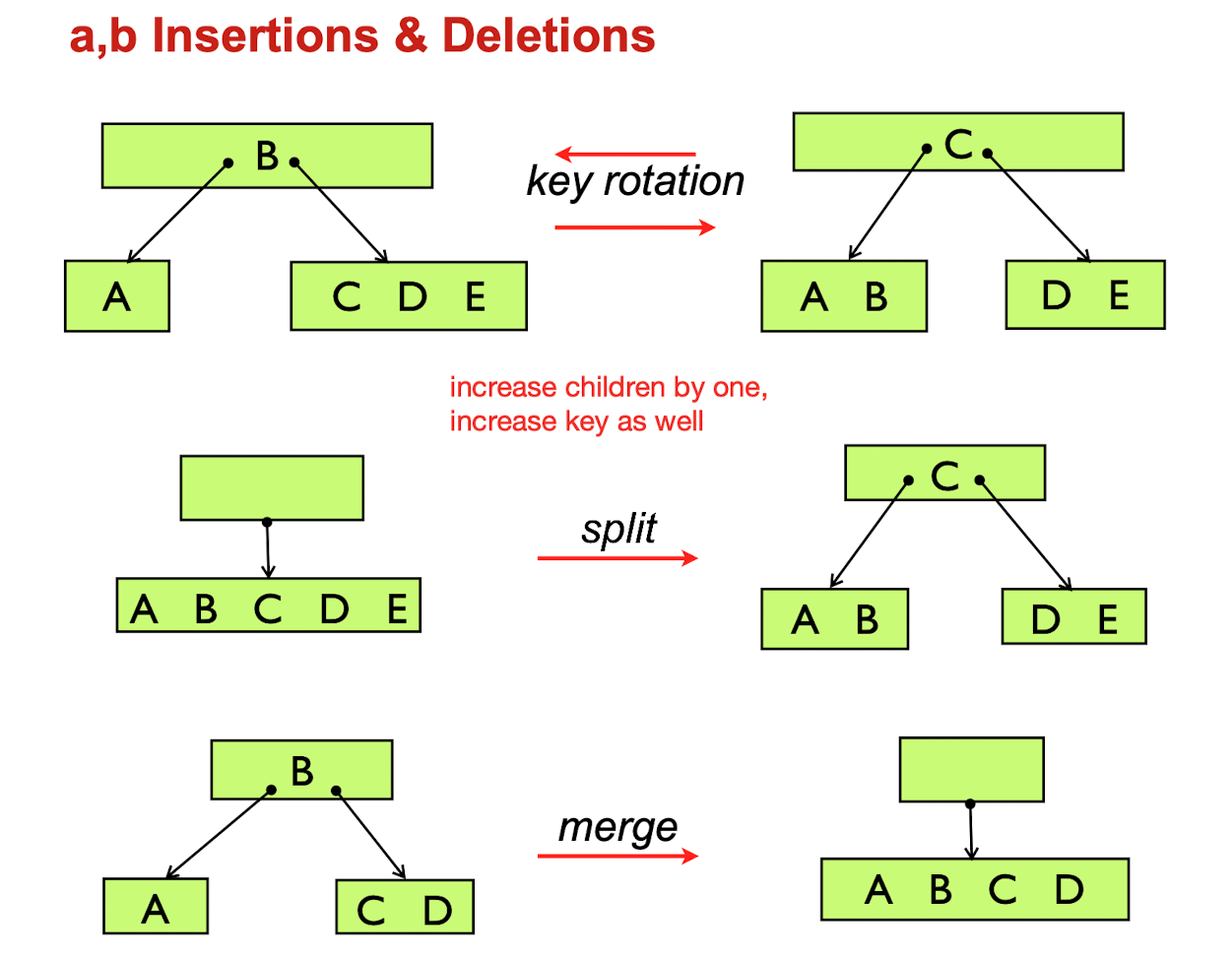
Key rotation to address the overflow problems

Condition 2

2,3 Tree insertion - When key rotation fails

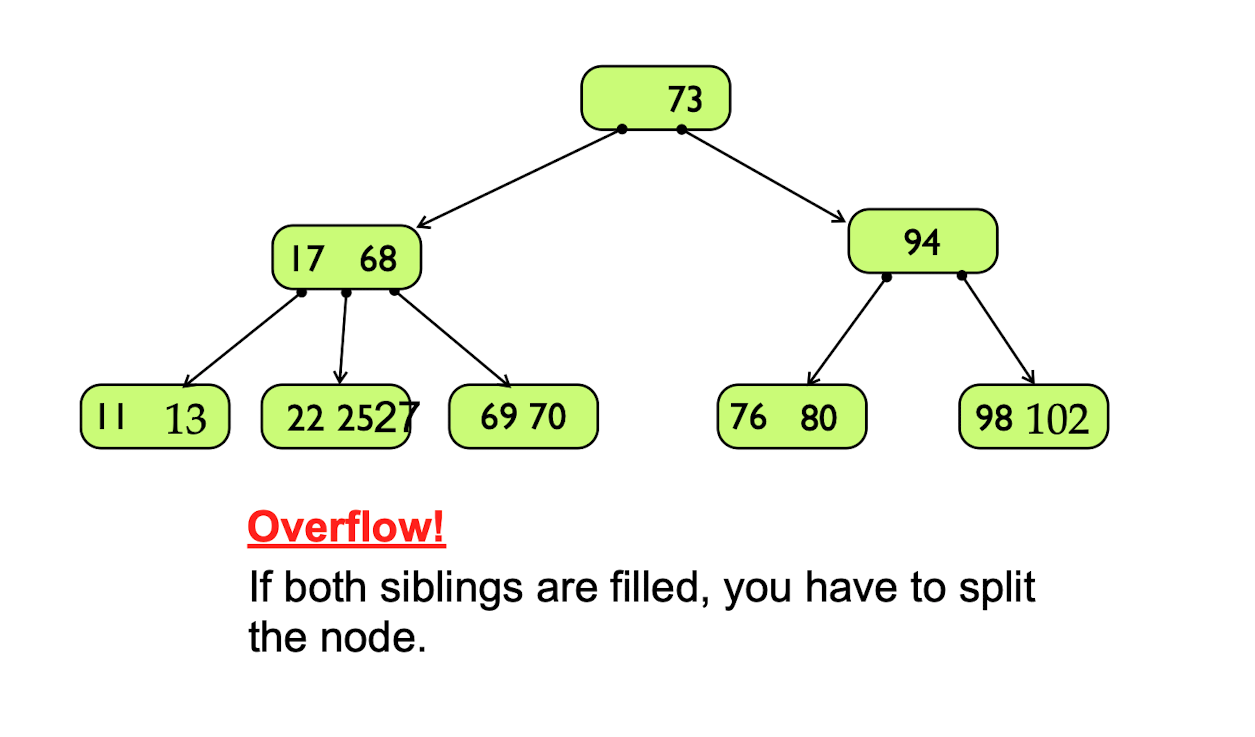
Solutions: may have to recursively split nodes, working back to the root

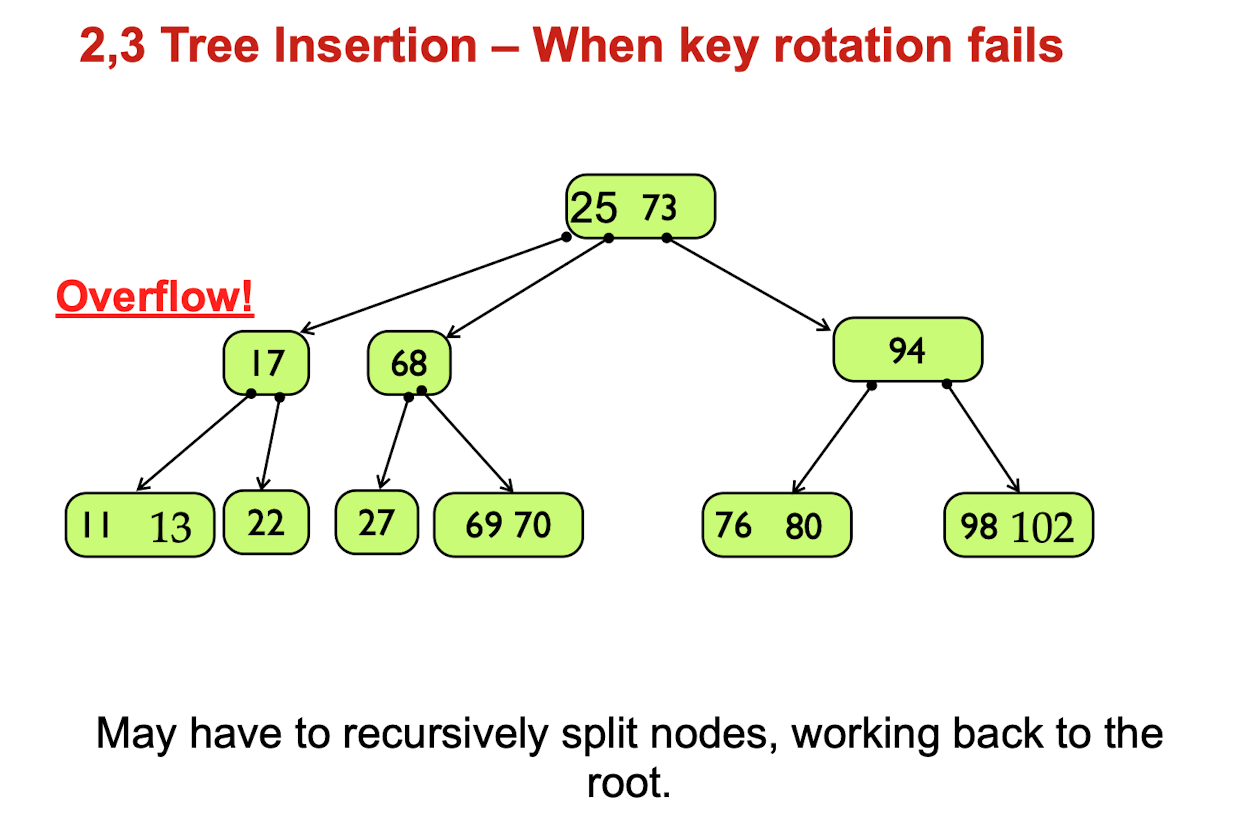
Condition 3

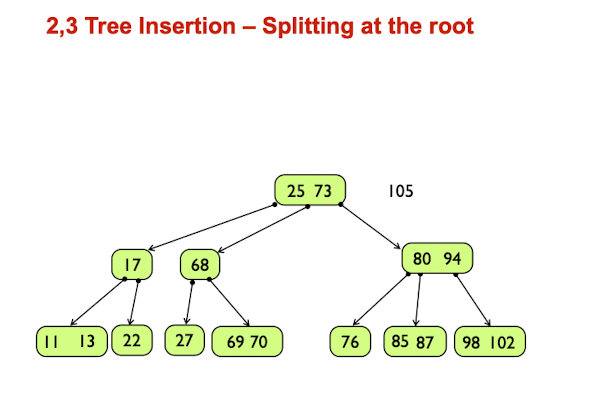
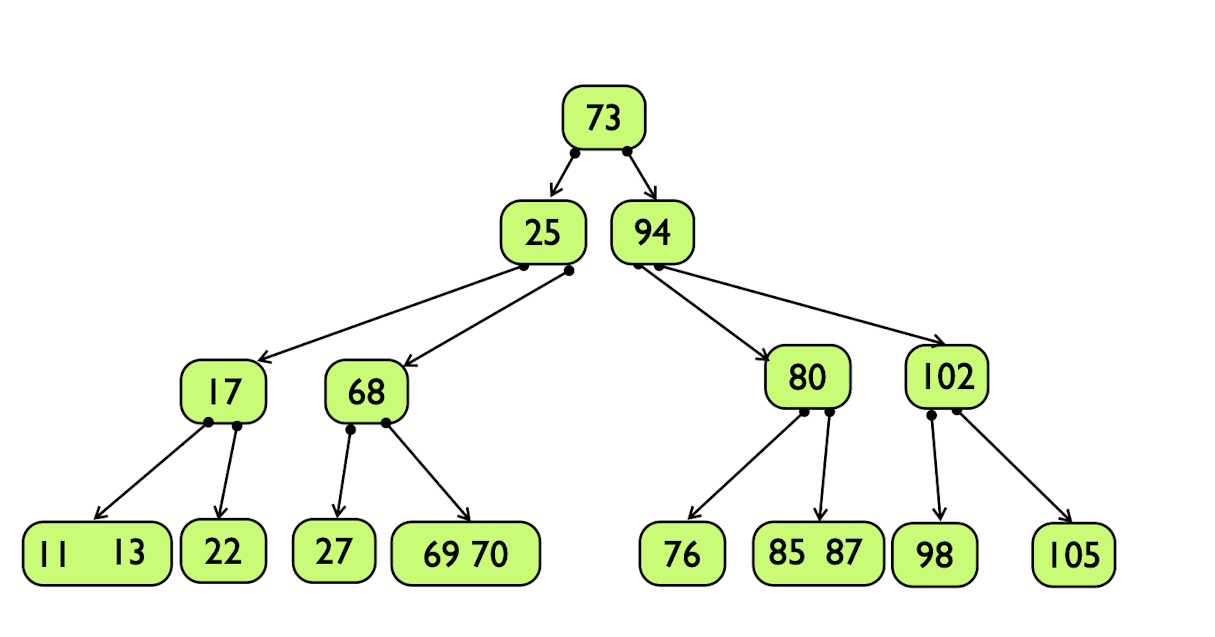
They would finally increase the depth by 1

a,b-trees

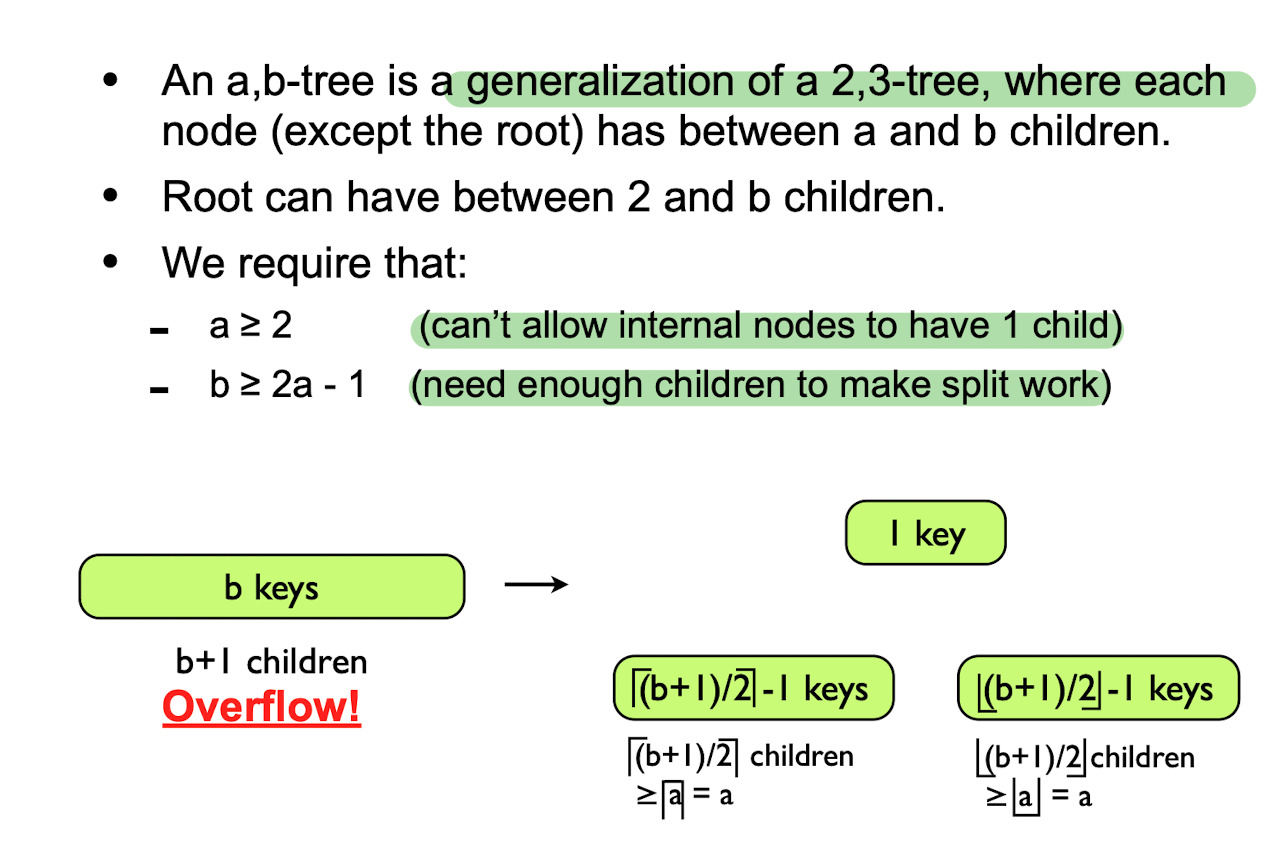
Insertion and deletion

B trees

• A B-tree of order b is an a,b-tree with b =2a-1.
  • In other words, we choose the largest allowed a
  • Each node (page) is at least 50% full
• Want to have large b if bringing a node into memory is slow (reading a disc block), but scanning the node once in memory is fast
• B is usually chosen to match characteristics of the device

e.g. B-tree of order 1023 has a = 512

• If this B-tree stores n = 10 million records, its height no more than O(log a n) = 2.58. So only around 3 blocks need to be read from disk

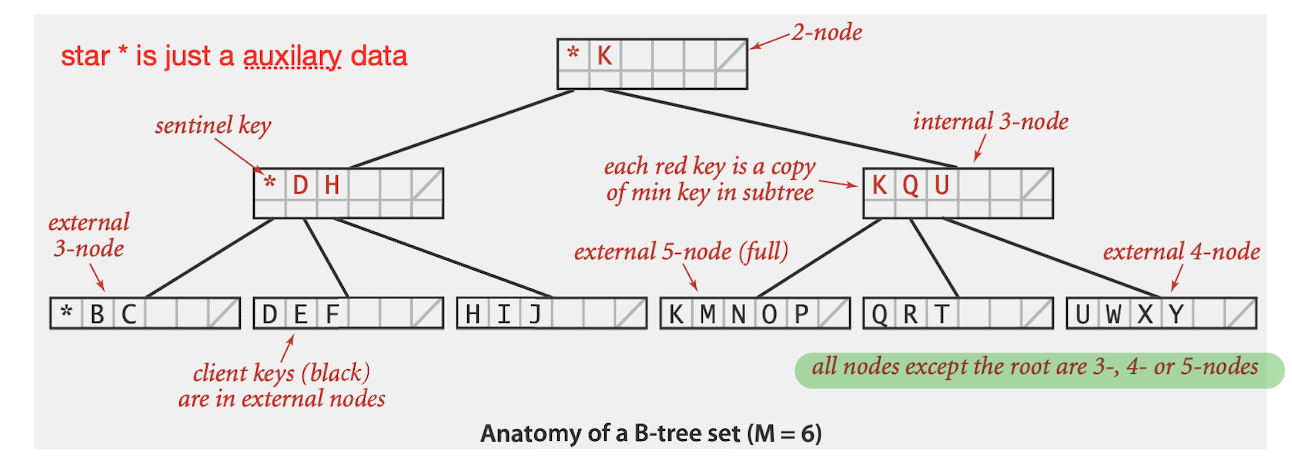
Definition

B-tree: Generalize 2-3 trees by allowing up to M-1 key-link pairs per node (M=2a)

• At least 2 key-link pairs at root
• At least M/2 key-link pairs in other nodes
• External nodes contain client keys
• Internal nodes contain copies of keys to guide search

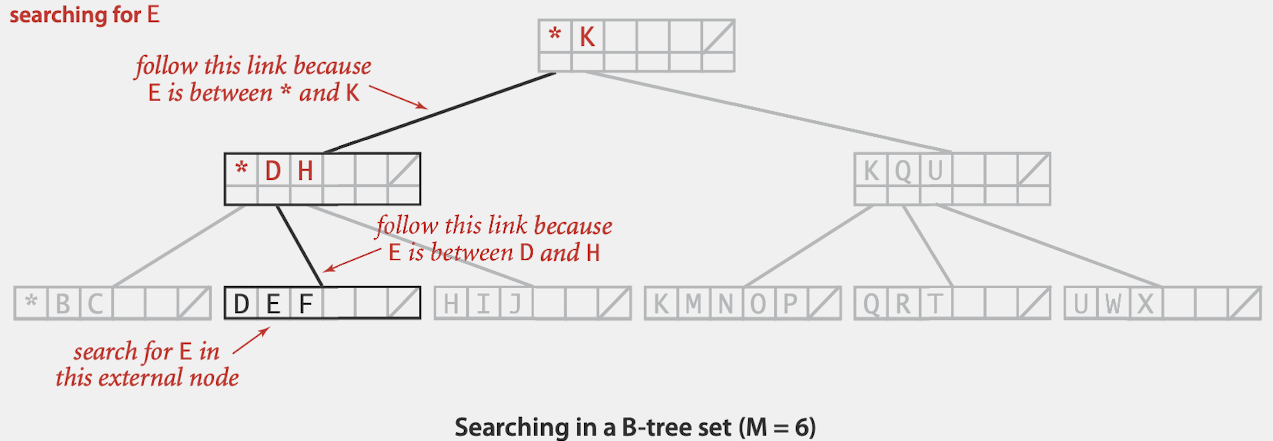
Searching in a B-tree

1. Start at root
2. Find interval for search key and take corresponding link
3. Serach terminates in external node.

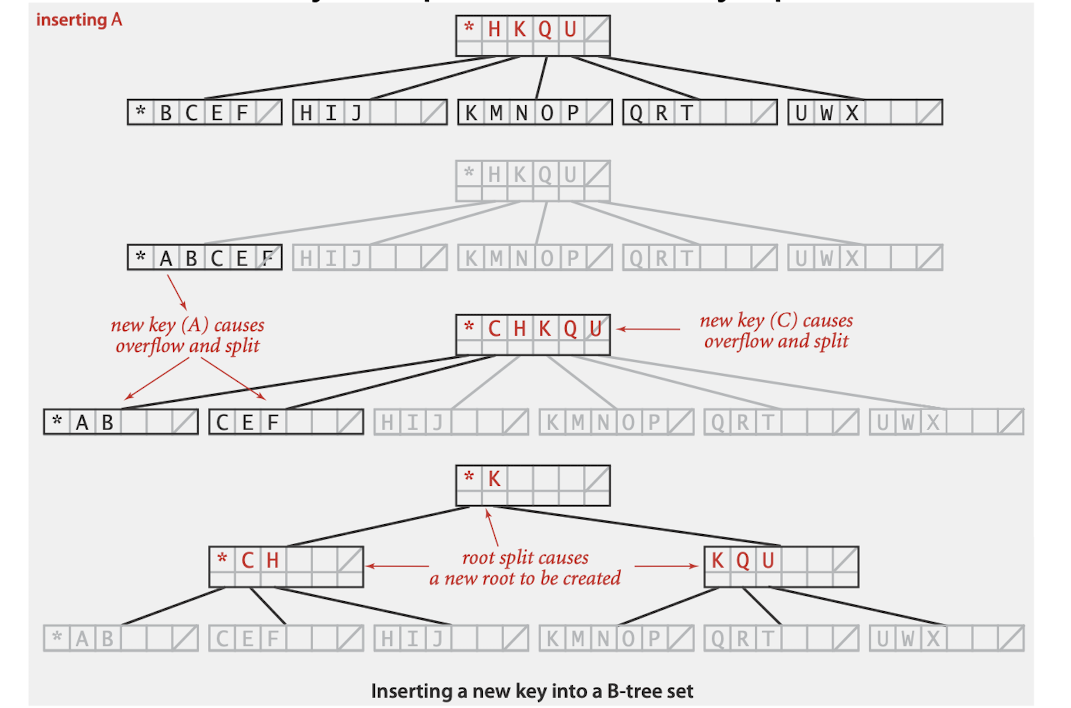
Insertion in a B-tree

1. Serach for new key
2. Insert at boots
3. Split nodes with M key-link pairs on the way up the tree

Balance in B-tree

• Proposition: A search or an insertion in a B-tree of order M with N keys requires between and probes
• All internal nodes (besides root) have between M/2 and M-1 links
• In practice. Number of probes is small, e.g. 4. (M = 1024; N = 62 billion, )

B is very large

1. Need to be able to find which subtree to traverse
2. Could linearly search through keys - technically constant time if b is a constant, but may be time consuming
3. Possible solution: Store a balanced tree (say a splay tree) at each node so that you can search for keys efficiently