skip list algo notes

Background

• Generalization of sorted linked lists
• Expected search time is O(logn)
• Randomized data structure
  • Use random coin flips to build the data structure

Perfect skip list

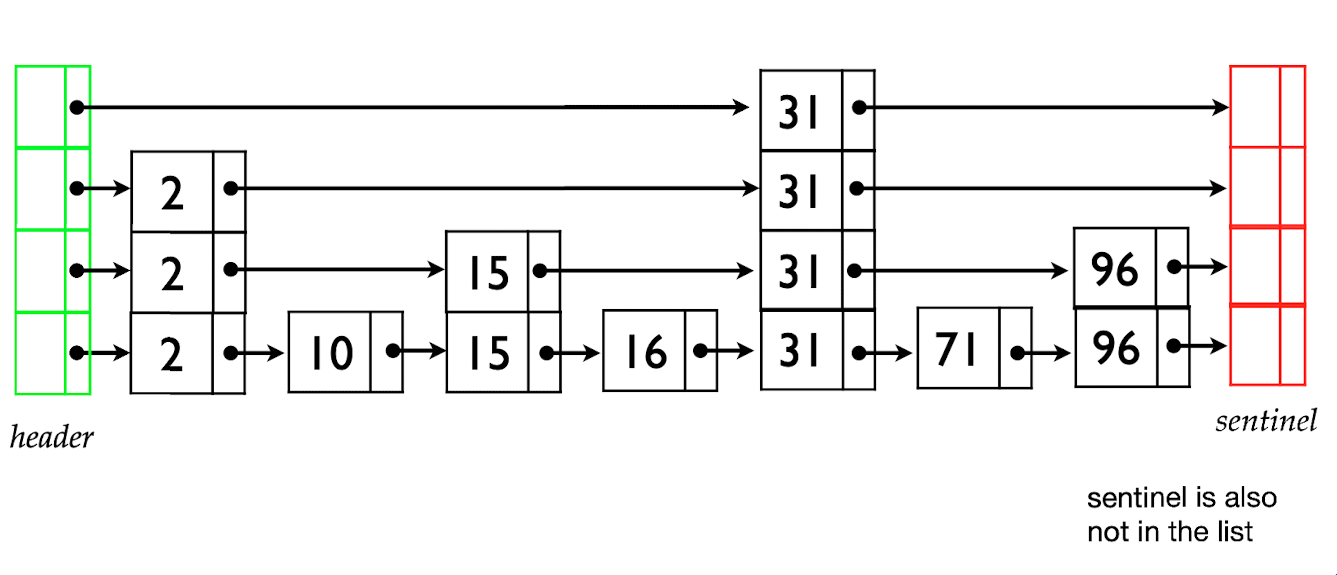
• Keys are stored in sorted order
• O(log n ) levels
• Each higher level contains 1/2 the elements of the level below it
• Header & sentinel nodes are in every level
• Nodes are of variable size range from 1 to O(log n ) pointers
• Pointers point to the start of each node
• Called skip list because higher level lists let you skip over many items

Find

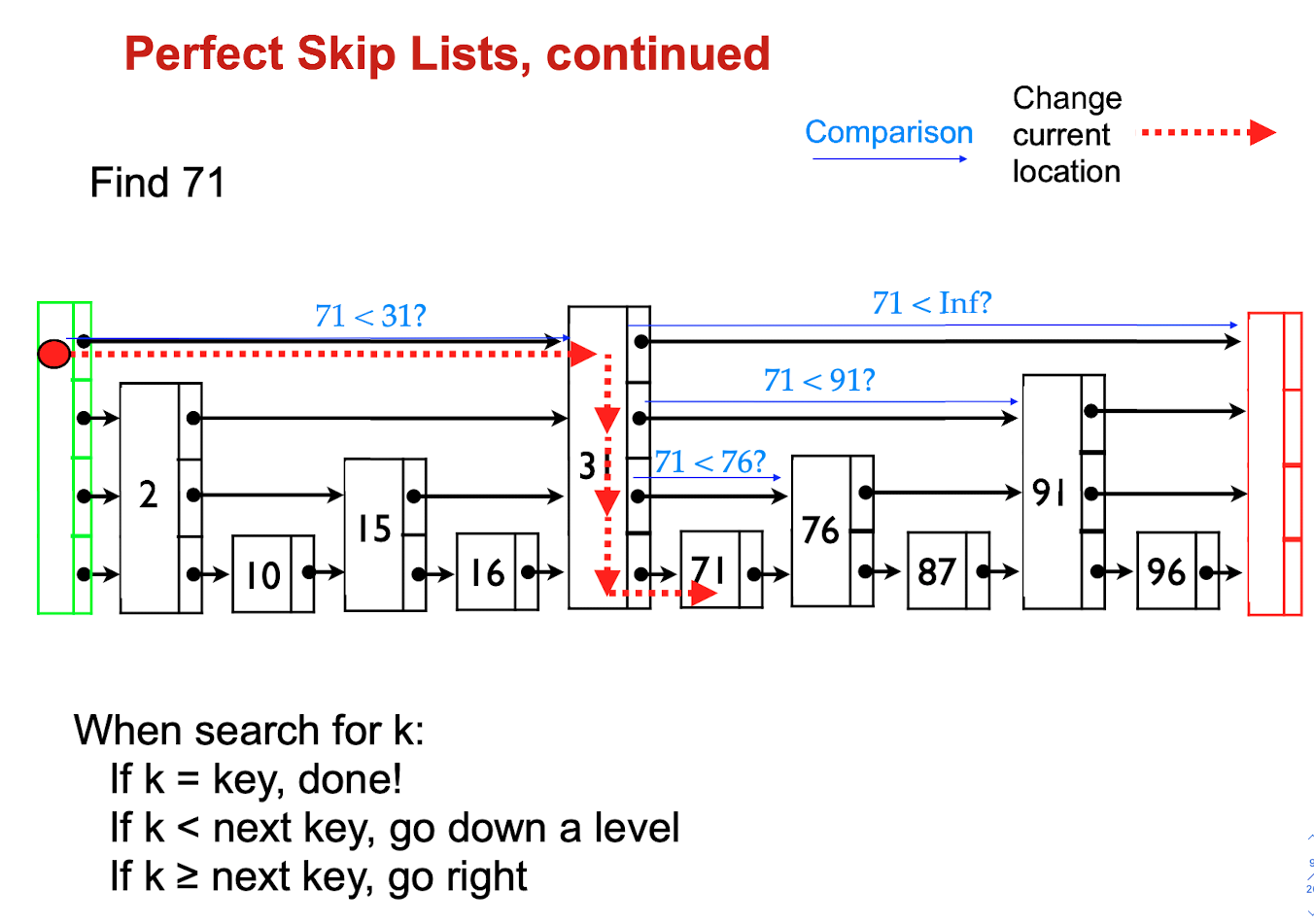
1. To find an item, we scan along the shortest list until we would “pass” the desired item
2. At that point, we drop down to a slightly more complete list at one level lower

Search time

• O(log n) levels because you cut the number of items in half at each level
• Will visit at most 2 nodes per level: If you visit more, then you could have done it on one level higher up
• Search time is O(log N)

Insert & Delete

1. Insert & delete might need to rearrange the entire list
2. Perfect Binary Search Trees, Perfect Skip Lists are too structured to support efficient updates

Resources

https://www.youtube.com/watch?v=Q9MdwzewSZg

Idea:

• Relax the requirement that each level has exactly half the items of the previous level
• Instead: design structure so that we expect 1/2 the items to be carried up to the next level
• Skip lists are a randomized data structure: the same sequence of inserts/deletes may produce different structures depending on the outcome of random coin flips

Randomization

1. Allows for some imbalance
2. Expected behavior (over the random choices) remains the same as with perfect skip lists

Idea: Each node is promoted to the next higher level with probability 1/2

• Expect 1/2 the nodes at level 1
• Expect 1/4 the nodes at level 2

Therefore, expect number of nodes at each levels the same as with perfect skip lists

Also: expect the promoted nodes will be well distributed across the list

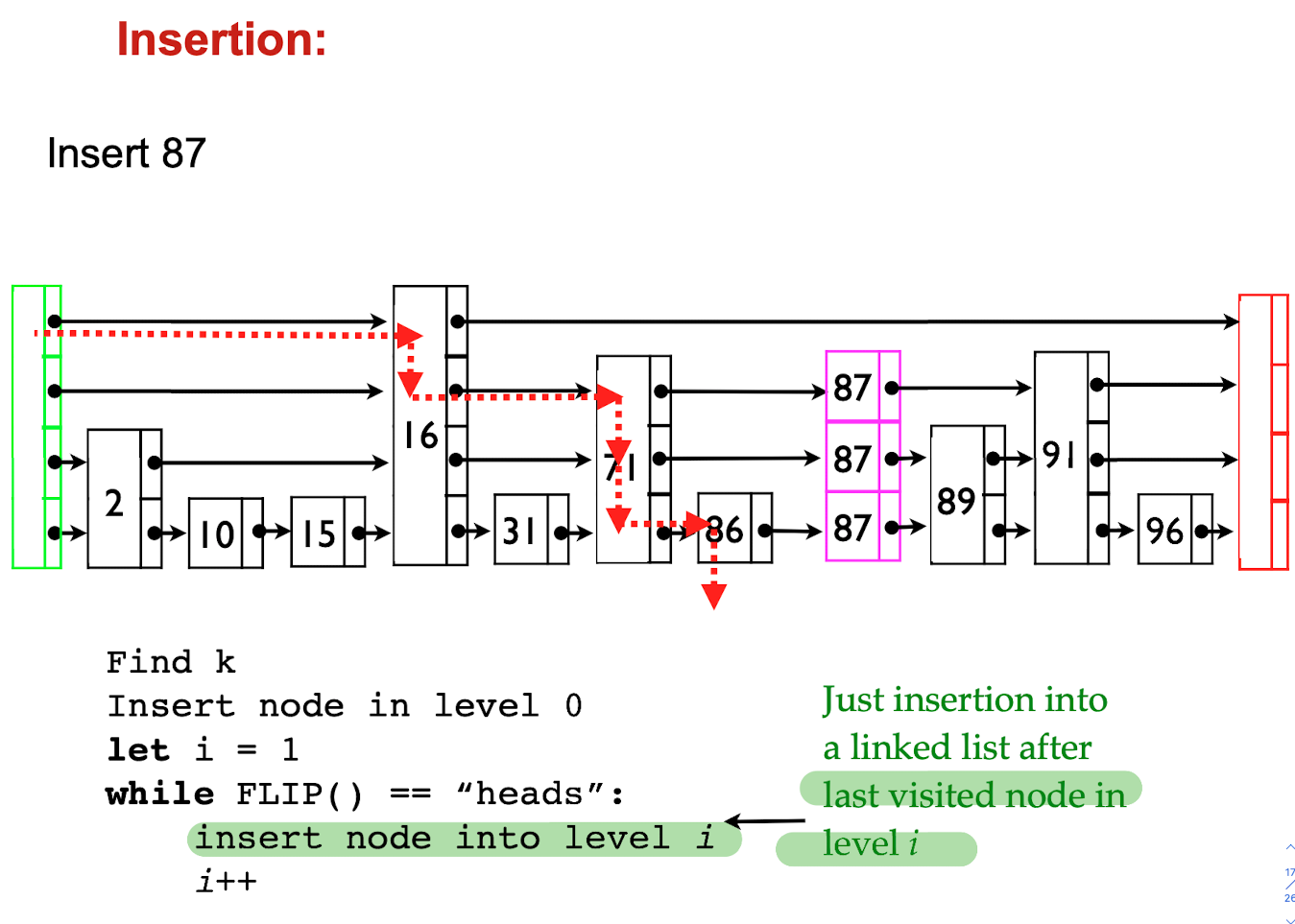
Noted here: the “heads” mean the coin’s head

No “bad” sequences

• We expect a randomized skip list to perform about as well as a perfect skip list.
• Some bad conditions might occur, but not often
  • The skip list will just be a linked list
  • The skip list will have every node at every level
  • These degenerate skip lists are very unlikely
• Level structure of a skip list is independent of the keys you insert
• Therefore, there are no “bad” key sequences that will lead to degenerate skip lists

Skip list analysis

Expected number of levels = O(log n)

• Expected nodes at level 1 would be n/2
• Expected nodes at level 2 would be n/4
• Expected nodes at level n would be 1

Backward analysis

Consider the reverse of the path you took to find k

Note that you always move up if you can (because you always enter a node from its topmost level when doing a find)

Probability

The probability that you can move up at a given step of the reverse talk would be 0.5

C(j) would be the expected number of steps to return to the start if we start at level j

Steps to go up j levels =

​ Make one step, then make either

- C(j-1) steps if this step went up because node was extended past level  j [Prob = 0.5]
- C(j) steps if this step went left because node wasn't extended up past j [Prob = 0.5]

Expected number of steps to walk up j levels is:

C(j) = 1 + 0.5C(j-1) + 0.5C(j)

=> C(j) = 2 + C(j-1)

Therefore, the expected number of steps at each level would be 2

• Expanding C(j) above would give us C(j) = 2j
• Since O(log n ) levels, we have O (log n) steps, which would follow the expectation

Implementation nodes

1. Node structure are of variable size
2. Once a node is created, it size won’t change
3. It’s often convenient to assume that you know the maximum number of levels in advance, but it is not a requirement