A* algorithm

Resources

https://www.redblobgames.com/pathfinding/a-star/introduction.html

https://stackabuse.com/graphs-in-java-a-star-algorithm/

A heuristic for shortest paths

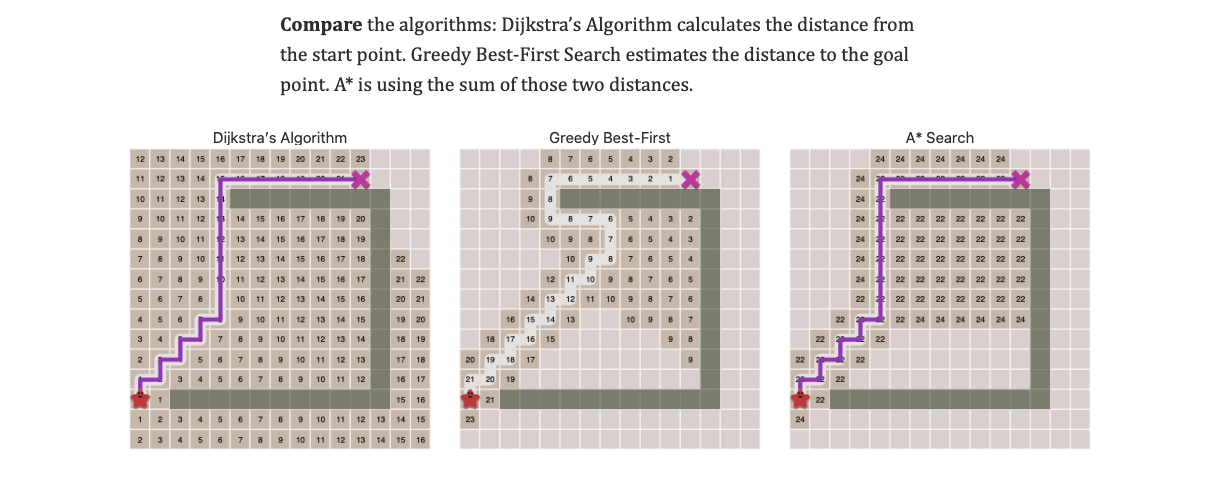
• Dijkstra’s algorithm assumes it knows noting about nodes it hasn’t reached during the algorithm
• Suppose instead we have h(u) which is an estimate of the distance from node u to t
• A plausible choice for h(u) if we were implementing a driving direction application h(u)= distance from u to t as the crow flies

A* algorithm

Maintain two values for every visited node

• g(u) = best distance from s to u found so far
• f(u) = g(u) + h(u) = estimate of the length of the best path from s to t through u

https://www.youtube.com/watch?v=-L-WgKMFuhE

Pseudocode

// A* Search Algorithm
1.  Initialize the open list
2.  Initialize the closed list
    put the starting node on the open 
    list (you can leave its f at zero)

3.  while the open list is not empty
    a) find the node with the least f on 
       the open list, call it "q"

    b) pop q off the open list
  
    c) generate q's 8 successors and set their 
       parents to q
   
    d) for each successor
        i) if successor is the goal, stop search
          successor.g = q.g + distance between 
                              successor and q
          successor.h = distance from goal to 
          successor (This can be done using many 
          ways, we will discuss three heuristics- 
          Manhattan, Diagonal and Euclidean 
          Heuristics)
          
          successor.f = successor.g + successor.h

        ii) if a node with the same position as 
            successor is in the OPEN list which has a 
           lower f than successor, skip this successor

        iii) if a node with the same position as 
            successor  is in the CLOSED list which has
            a lower f than successor, skip this successor
            otherwise, add  the node to the open list
     end (for loop)
  
    e) push q on the closed list
    end (while loop)

Python implementation

frontier = PriorityQueue()
frontier.put(start, 0)
came_from = dict()
cost_so_far = dict()
came_from[start] = None
cost_so_far[start] = 0

while not frontier.empty():
   current = frontier.get()

   if current == goal:
      break
   
   for next in graph.neighbors(current):
      new_cost = cost_so_far[current] + graph.cost(current, next)
      if next not in cost_so_far or new_cost < cost_so_far[next]:
         cost_so_far[next] = new_cost
         priority = new_cost + heuristic(goal, next)
         frontier.put(next, priority)
         came_from[next] = current

Choice of h(u)

Definition (Admissible):

Let h*(u) be the real shortest distance from u to t. A heuristic h(u) is admissible if h(u)h*(u) for all u

• When h(u) = 0 for all u: A* is equivalent to Dijkstra’s algorithm

Theorem

If h(u) is admissible, then A* is guaranteed to find an optimal route to the destination t

TSP