Dijkstra algorithm

Helper resources

https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-in-java-using-priorityqueue/

https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-using-set-in-stl/ 最像课上教的 (heap based Dijkstra algorithm)

https://www.scaler.com/topics/data-structures/dijkstra-algorithm/

Dijkstra’s Shortest path problem

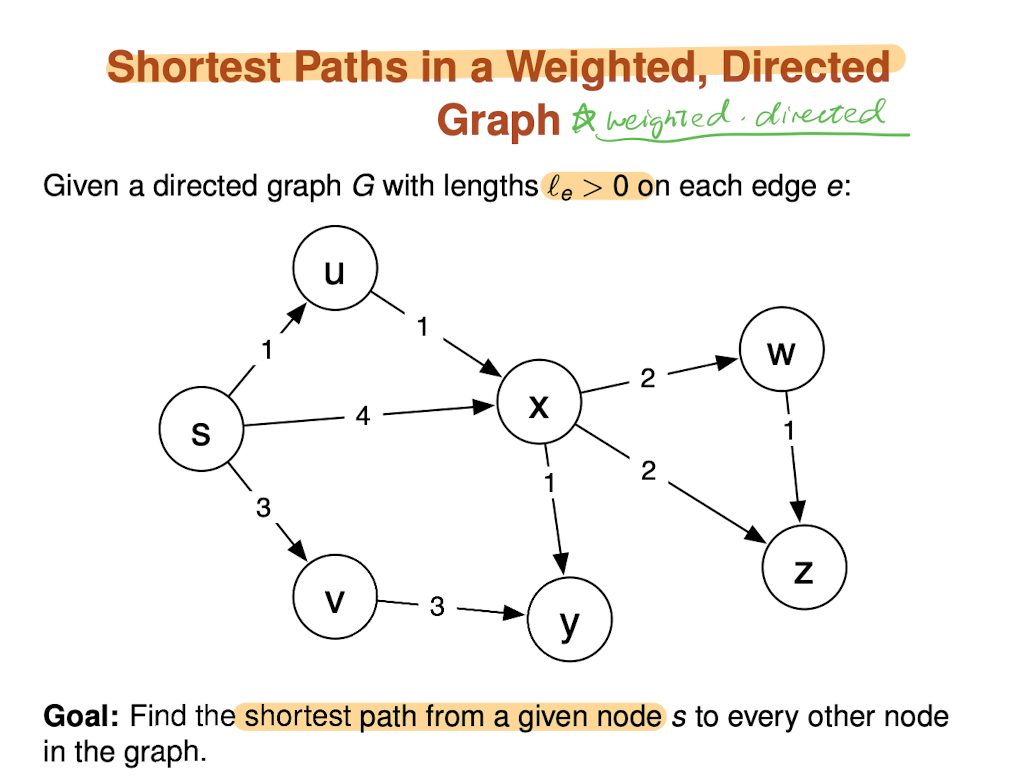
Which kind of problem to solve

Given a graph and a source vertex in the graph, find the shortest paths from the source to all vertices in the given graph.

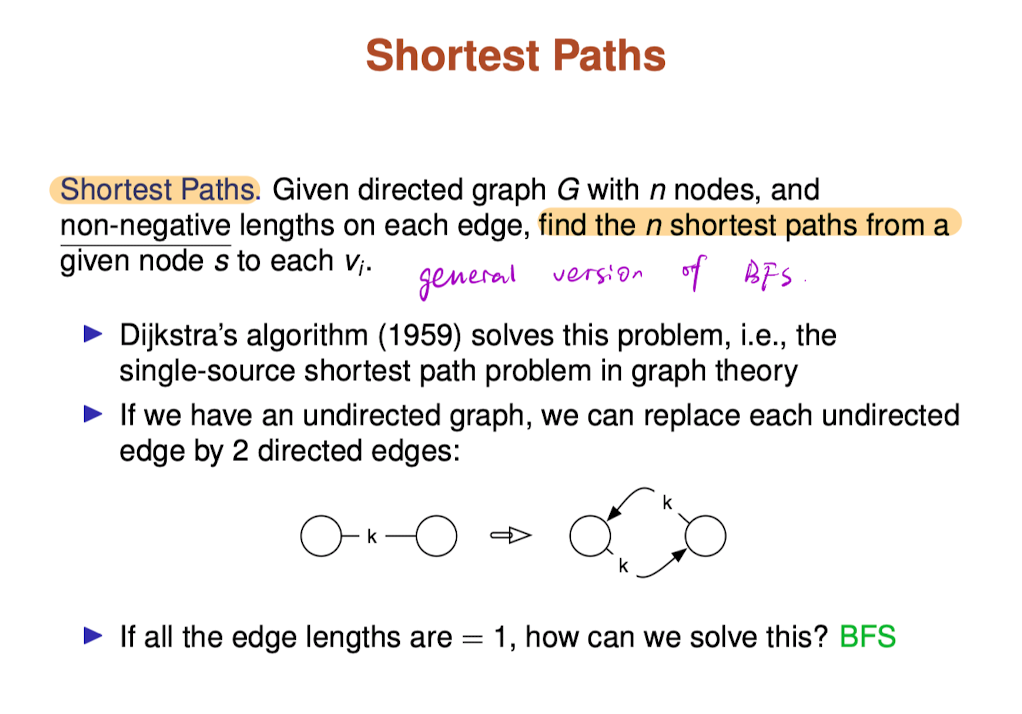
Shortest Paths and BFS

1. BFS is an algorithm for finding shortest (link-distance) paths from a single source vertex to all other vertices
2. BFS processes vertices in increasing order of their distance from the root vertex

Tree growing again

nextEdge for shortest path

1. Let u be some node that we have already visited (it will be in S)
2. Let d(u) be the length of the s - u path found for node u s
3. nextEdge: return the frontier edge (u,v) for which d(u) + length(u,v) is minimized
4. The d(u) term is the difference from Prim’s algorithm

Implementation

Heap pseudocode

Output:

Dijkstra’s algorithm would output a list of parent-child relationships (array p) and a list of source-to-node distance (array d)

Pseudocode from wiki

1) Initialize distances of all vertices as infinite.

2) Create an empty set.  Every item of set is a pair
  (weight, vertex). Weight (or distance) is used used
  as first item  of pair as first item is by default 
  used to compare two pairs.

3) Insert source vertex into the set and make its
   distance as 0.

4) While Set doesn't become empty, do following
    a) Extract minimum distance vertex from Set. 
       Let the extracted vertex be u.
    b) Loop through all adjacent of u and do 
       following for every vertex v.

           // If there is a shorter path to v
           // through u. 
           If dist[v] > dist[u] + weight(u, v)

               (i) Update distance of v, i.e., do
                     dist[v] = dist[u] + weight(u, v)
               (i) If v is in set, update its distance
                   in set by removing it first, then
                   inserting with new distance
               (ii) If v is not in set, then insert
                    it in set with new distance
               
5) Print distance array dist[] to print all shortest
   paths. 

Drawback: while finding the shortest path as listed as follows as we need to find the least cost path by going through the whole cost array.

It can be applied to both directed and undirected graph. Here is why:

An undirected graph is basically the same as a directed graph with bidirectional connections (= two connections in opposite directions) between the connected nodes.

So you don’t really have to do anything to make it work for an undirected graph. You only need to know all of the nodes that can be reached from every given node through e.g. an adjacency list.

Java implementation

package cn.itcast.algorithm.graph;

import cn.itcast.algorithm.linear.Queue;
import cn.itcast.algorithm.priority.IndexMinPriorityQueue;


public class DijkstraSP {
    //索引代表顶点，值表示从顶点s到当前顶点的最短路径上的最后一条边
    private DirectedEdge[] edgeTo;
    //索引代表顶点，值从顶点s到当前顶点的最短路径的总权重
    private double[] distTo;
    //存放树中顶点与非树中顶点之间的有效横切边
    private IndexMinPriorityQueue<Double> pq;

    //根据一副加权有向图G和顶点s，创建一个计算顶点为s的最短路径树对象
    public DijkstraSP(EdgeWeightedDigraph G, int s){
        //初始化edgeTo
        this.edgeTo = new DirectedEdge[G.V()];
        //初始化distTo
        this.distTo = new double[G.V()];
        for (int i = 0; i < distTo.length; i++) {
            distTo[i] = Double.POSITIVE_INFINITY;
        }
        //初始化pq
        this.pq = new IndexMinPriorityQueue<>(G.V());

        //找到图G中以顶点s为起点的最短路径树

        //默认让顶点s进入到最短路径树中
        distTo[s] = 0.0;
        pq.insert(s,0.0);

        //遍历pq

        while(!pq.isEmpty()){
            relax(G,pq.delMin());
        }

    }

    //松弛图G中的顶点v
    private void relax(EdgeWeightedDigraph G, int v){

        for (DirectedEdge edge : G.adj(v)) {
            //获取到该边的终点w
            int w = edge.to();

            //通过松弛技术，判断从起点s到顶点w的最短路径是否需要先从顶点s到顶点v，然后再由顶点v到顶点w
            if (distTo(v)+edge.weight()<distTo(w)){
                distTo[w] = distTo[v]+edge.weight();
                edgeTo[w] = edge;

                //判断pq中是否已经存在顶点w，如果存在，则更新权重，如果不存在，则直接添加
                if (pq.contains(w)){
                    pq.changeItem(w,distTo(w));
                }else{
                    pq.insert(w,distTo(w));
                }

            }
        }

    }

    //获取从顶点s到顶点v的最短路径的总权重
    public double distTo(int v){
        return distTo[v];
    }

    //判断从顶点s到顶点v是否可达
    public boolean hasPathTo(int v){
        return distTo[v]<Double.POSITIVE_INFINITY;
    }

    //查询从起点s到顶点v的最短路径中所有的边
    public Queue<DirectedEdge> pathTo(int v){
        //判断从顶点s到顶点v是否可达，如果不可达，直接返回null
        if (!hasPathTo(v)){
            return null;
        }

        //创建队列对象
        Queue<DirectedEdge> allEdges = new Queue<>();

        while (true){
            DirectedEdge e = edgeTo[v];
            if (e==null){
                break;
            }

            allEdges.enqueue(e);

            v = e.from();
        }


        return allEdges;
    }

}

Array based

Algorithm
1) Create a set sptSet (shortest path tree set) that keeps track of vertices included in the shortest-path tree, i.e., whose minimum distance from the source is calculated and finalized. Initially, this set is empty.
2) Assign a distance value to all vertices in the input graph. Initialize all distance values as INFINITE. Assign distance value as 0 for the source vertex so that it is picked first.
3) While sptSet doesn’t include all vertices
….a) Pick a vertex u which is not there in sptSet and has a minimum distance value.
….b) Include u to sptSet.
….c) Update distance value of all adjacent vertices of u. To update the distance values, iterate through all adjacent vertices. For every adjacent vertex v, if the sum of distance value of u (from source) and weight of edge u-v, is less than the distance value of v, then update the distance value of v.

package graph;

// A Java program for Dijkstra's single source shortest path algorithm.
// The program is for adjacency matrix representation of the graph
import java.util.*;
import java.lang.*;
import java.io.*;

class ShortestPath {
    // A utility function to find the vertex with minimum distance value,
    // from the set of vertices not yet included in shortest path tree
    static final int V = 9;
    int minDistance(int dist[], Boolean sptSet[])
    {
        // Initialize min value
        int min = Integer.MAX_VALUE, min_index = -1;

        for (int v = 0; v < V; v++)
            if (sptSet[v] == false && dist[v] <= min) {
                min = dist[v];
                min_index = v;
            }

        return min_index;
    }

    // A utility function to print the constructed distance array
    void printSolution(int dist[])
    {
        System.out.println("Vertex \t\t Distance from Source");
        for (int i = 0; i < V; i++)
            System.out.println(i + " \t\t " + dist[i]);
    }

    // Function that implements Dijkstra's single source shortest path
    // algorithm for a graph represented using adjacency matrix
    // representation
    void dijkstra(int graph[][], int src)
    {
        int dist[] = new int[V]; // The output array. dist[i] will hold
        // the shortest distance from src to i

        // sptSet[i] will true if vertex i is included in shortest
        // path tree or shortest distance from src to i is finalized
        Boolean sptSet[] = new Boolean[V];

        // Initialize all distances as INFINITE and stpSet[] as false
        for (int i = 0; i < V; i++) {
            dist[i] = Integer.MAX_VALUE;
            sptSet[i] = false;
        }

        // Distance of source vertex from itself is always 0
        dist[src] = 0;

        // Find shortest path for all vertices
        for (int count = 0; count < V - 1; count++) {
            // Pick the minimum distance vertex from the set of vertices
            // not yet processed. u is always equal to src in first
            // iteration.
            int u = minDistance(dist, sptSet);

            // Mark the picked vertex as processed
            sptSet[u] = true;

            // Update dist value of the adjacent vertices of the
            // picked vertex.
            for (int v = 0; v < V; v++)

                // Update dist[v] only if is not in sptSet, there is an
                // edge from u to v, and total weight of path from src to
                // v through u is smaller than current value of dist[v]
                if (!sptSet[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE && dist[u] + graph[u][v] < dist[v])
                    dist[v] = dist[u] + graph[u][v];
        }

        // print the constructed distance array
        printSolution(dist);
    }

    // Driver method
    public static void main(String[] args)
    {
        /* Let us create the example graph discussed above */
        int graph[][] = new int[][] { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
                { 4, 0, 8, 0, 0, 0, 0, 11, 0 },
                { 0, 8, 0, 7, 0, 4, 0, 0, 2 },
                { 0, 0, 7, 0, 9, 14, 0, 0, 0 },
                { 0, 0, 0, 9, 0, 10, 0, 0, 0 },
                { 0, 0, 4, 14, 10, 0, 2, 0, 0 },
                { 0, 0, 0, 0, 0, 2, 0, 1, 6 },
                { 8, 11, 0, 0, 0, 0, 1, 0, 7 },
                { 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
        ShortestPath t = new ShortestPath();
        t.dijkstra(graph, 0);
    }
}
// This code is contributed by Aakash Hasija

Original figures

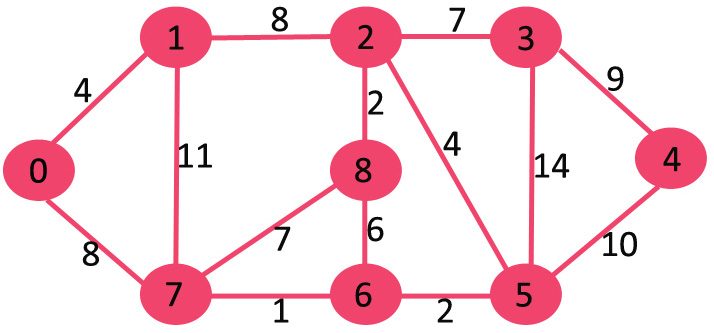
Results

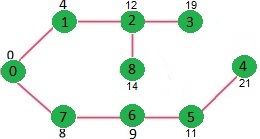
Vertex 		 Distance from Source
0 		 0
1 		 4
2 		 12
3 		 19
4 		 21
5 		 11
6 		 9
7 		 8
8 		 14

Run time analysis

1. Every edge is processed in the for loop at most once
2. In response to that processing, we may either
   1. Do nothing
   2. Insert an item into the heap of at most V items; O(log|V|)
   3. Reduce the key of an item in a heap of at most |V| items; O(log|V|)

Total Time complexity : O(E*log(V))

Comparison with BellmanFord

Summary

Dijkstra only process the minimum edge, while Bellman-ford process every edge. This makes Bell-man ford slower, but it can handle negative edges

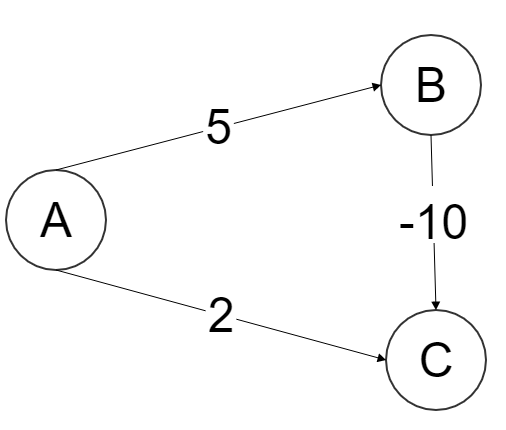
Consider the graph shown below with the source as Vertex A. First try running Dijkstra’s algorithm yourself on it.

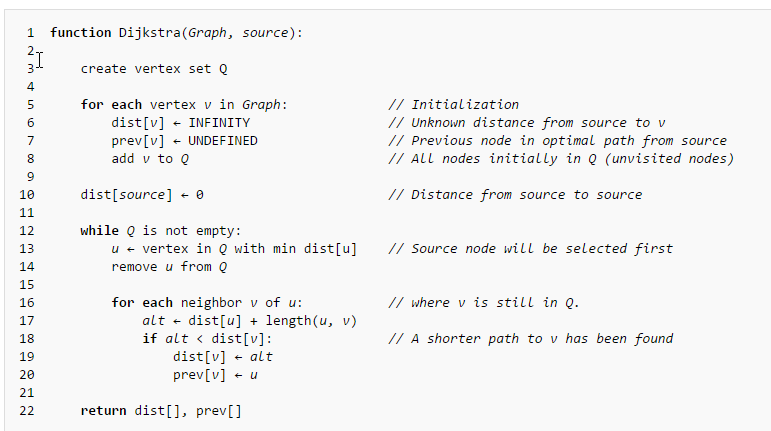
When I refer to Dijkstra’s algorithm in my explanation I will be talking about the Dijkstra’s Algorithm as implemented below,

So starting out the values (the distance from the source to the vertex) initially assigned to each vertex are,

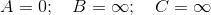
We first extract the vertex in Q = [A,B,C] which has smallest value, i.e. A, after which Q = [B, C]. Note A has a directed edge to B and C, also both of them are in Q, therefore we update both of those values,

Now we extract C as (2<5), now Q = [B]. Note that C is connected to nothing, so line16 loop doesn’t run.

Finally we extract B, after which . Note B has a directed edge to C but C isn’t present in Q therefore we again don’t enter the for loop in line16,

So we end up with the distances as

Note how this is wrong as the shortest distance from A to C is 5 + -10 = -5, when you go .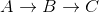

So for this graph Dijkstra’s Algorithm wrongly computes the distance from A to C.

This happens because Dijkstra’s Algorithm does not try to find a shorter path to vertices which are already extracted from Q.

What the line16 loop is doing is taking the vertex u and saying “hey looks like we can go to v from source via u, is that (alt or alternative) distance any better than the current dist[v] we got? If so lets update dist[v]“

Note that in line16 they check all neighbors v (i.e. a directed edge exists from u to v), of u which are still in Q. In line14 they remove visited notes from Q. So if x is a visited neighbour of u, the path 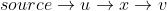is not even considered as a possible shorter way from source to v.

In our example above, C was a visited neighbour of B, thus the path was not considered, leaving the current shortest path unchanged.

This is actually useful if the edge weights are all positive numbers, because then we wouldn’t waste our time considering paths that can’t be shorter.

So I say that when running this algorithm if x is extracted from Q before y, then its not possible to find a path - which is shorter. Let me explain this with an example,

As y has just been extracted and x had been extracted before itself, then dist[y] > dist[x] because otherwise y would have been extracted before x. (line 13 min distance first)

And as we already assumed that the edge weights are positive, i.e. length(x,y)>0. So the alternative distance (alt) via y is always sure to be greater, i.e. dist[y] + length(x,y)> dist[x]. So the value of dist[x] would not have been updated even if y was considered as a path to x, thus we conclude that it makes sense to only consider neighbors of y which are still in Q (note comment in line16)

But this thing hinges on our assumption of positive edge length, if length(u,v)<0 then depending on how negative that edge is we might replace the dist[x] after the comparison in line18.

So any dist[x] calculation we make will be incorrect if x is removed before all vertices v - such that x is a neighbour of v with negative edge connecting them - is removed.

Because each of those v vertices is the second last vertex on a potential “better” path from source to x, which is discarded by Dijkstra’s algorithm.

So in the example I gave above, the mistake was because C was removed before B was removed. While that C was a neighbour of B with a negative edge!

Just to clarify, B and C are A’s neighbours. B has a single neighbour C and C has no neighbours. length(a,b) is the edge length between the vertices a and b.