Union Find algo notes

Requirements:

How could we check if adding an edge {u, v} would create a cycle

1. Create a cycle if u and v are already in the same component
2. Start with a component for each node
3. Components merge when we add an edge
4. Need to find a way to check if u and v are in same component and to merge two components into one

Data structure: Union Find

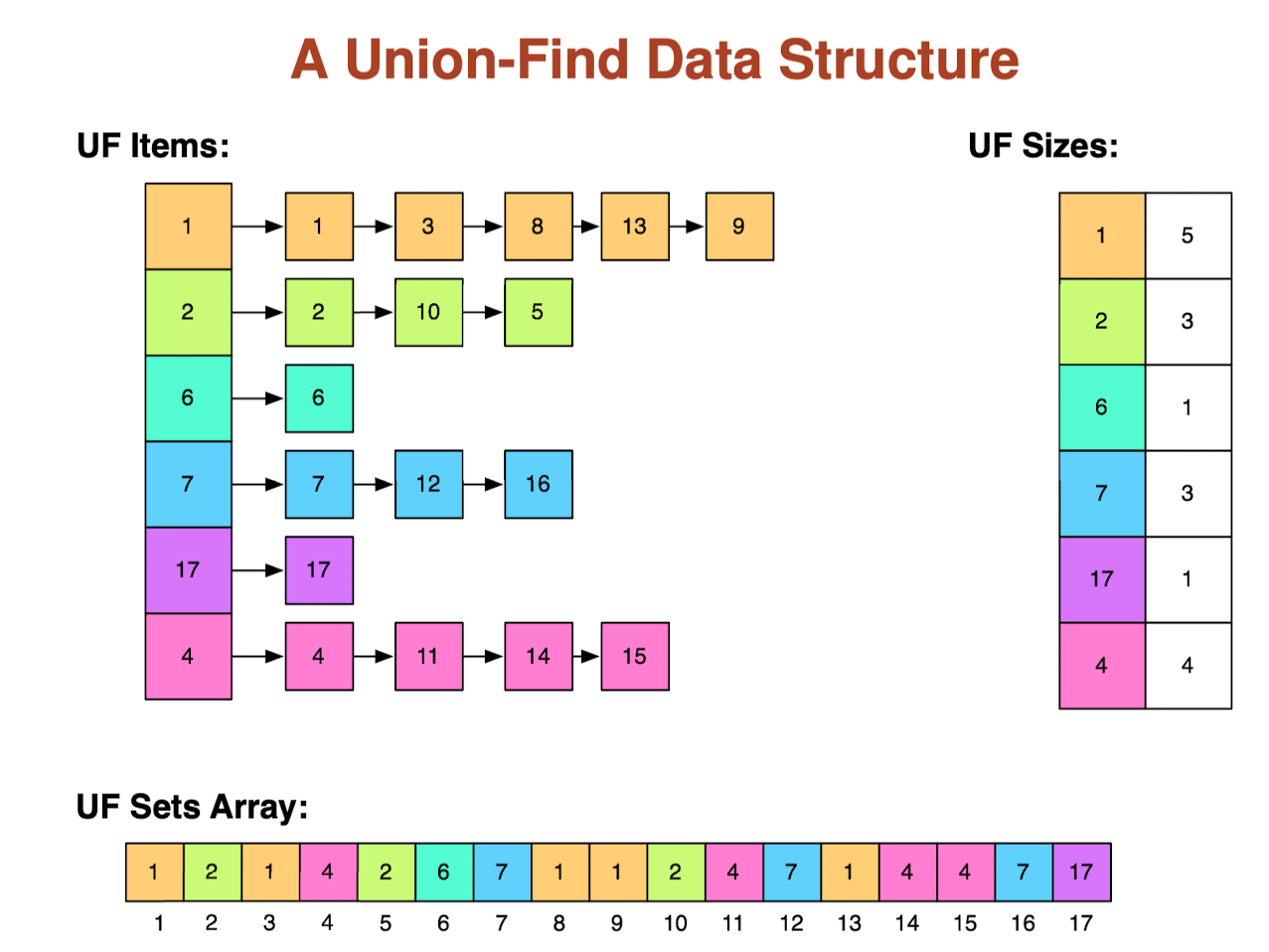
Array based UF

• MakeUnionFind(S):
  • create the data structure containing S sets, each containing one item from S.
  • Take time proportional to the size of S
• Find(i):
  • return the “name” of the set containing item i
  • Takes a constant amount of time
• Union(a,b):
  • merge the sets with names a and b into a single set
  • Use the “size” array to decide which set is smaller.
    • Assume x is smaller, walk down elements in set x, setting sets[i] = y. Set size[y] = size[y]+size[x]. Make y point to start of x list and end of x list point to y.

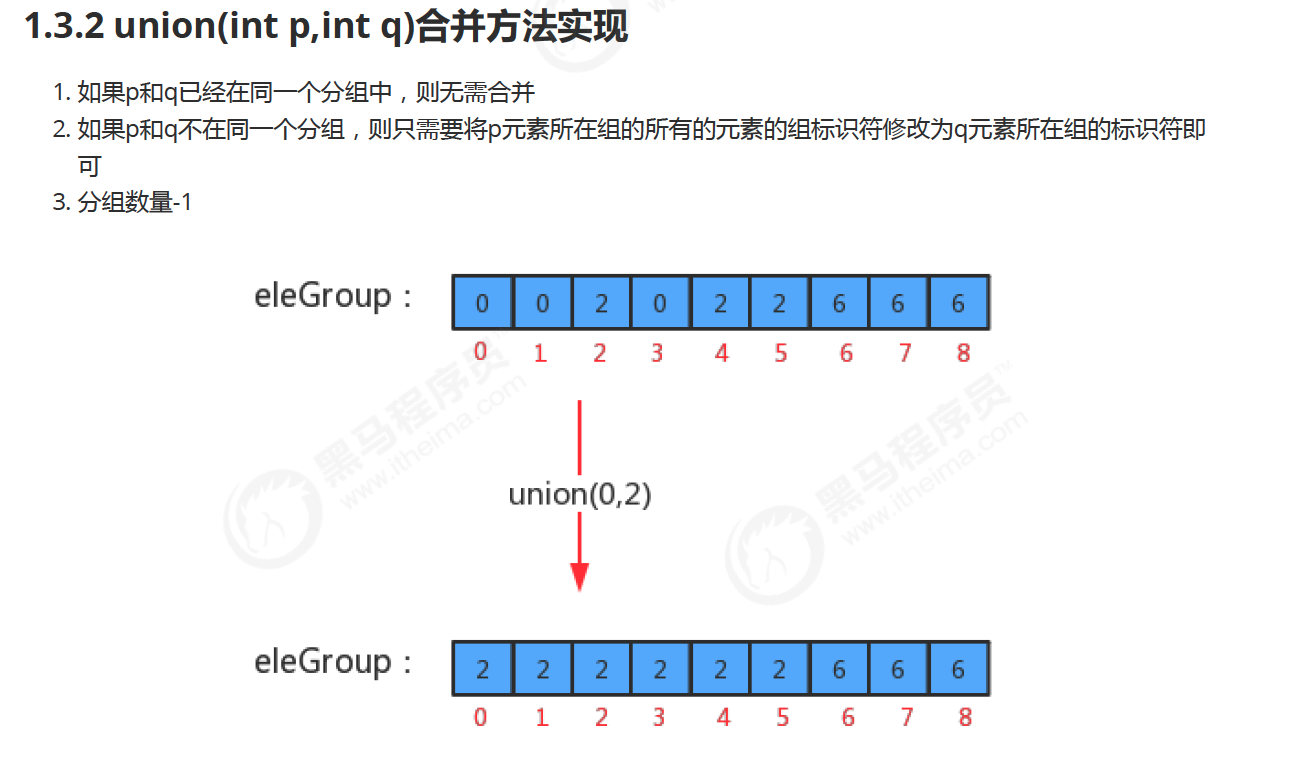
package cn.itcast.algorithm.uf;

public class UF {
    //记录结点元素和该元素所在分组的标识
    private int[] eleAndGroup;
    //记录并查集中数据的分组个数
    private int count;
    //初始化并查集
    public UF(int N){
        //初始化分组的数量,默认情况下，有N个分组
        this.count = N;

        //初始化eleAndGroup数组
        this.eleAndGroup = new int[N];

        //初始化eleAndGroup中的元素及其所在的组的标识符,让eleAndGroup数组的索引作为并查集的每个结点的元素，并且让每个索引处的值(该元素所在的组的标识符)就是该索引
        for (int i = 0; i < eleAndGroup.length; i++) {
            eleAndGroup[i] = i;
        }

    }

    //获取当前并查集中的数据有多少个分组
    public int count(){
        return count;
    }

    //元素p所在分组的标识符
    public int find(int p){
        return eleAndGroup[p];
    }

    //判断并查集中元素p和元素q是否在同一分组中
    public boolean connected(int p,int q){
        return find(p) == find(q);
    }

    //把p元素所在分组和q元素所在分组合并
    public void union(int p,int q){
        //判断元素q和p是否已经在同一分组中，如果已经在同一分组中，则结束方法就可以了
        if (connected(p,q)){
            return;
        }

        //找到p所在分组的标识符
        int pGroup = find(p);

        //找到q所在分组的标识符
        int qGroup = find(q);

        //合并组：让p所在组的所有元素的组标识符变为q所在分组的标识符
        for (int i = 0; i < eleAndGroup.length; i++) {
            if (eleAndGroup[i]==pGroup){
                eleAndGroup[i] = qGroup;
            }
        }

        //分组个数-1
        this.count--;

    }

}

Run time of array-based Union-Find

Any sequence of k union operations on a collection of n items take time at most proportional to klogk

Proof: After k unions, at most 2k items have been involved in a union

We upper bound the number of times set[v] changes for any v:

• Every time set[v] changes, the size of the set that v is at least doubles
• Set[v] can have changed at most

In summary: at most 2k items have been modified at all, and each was updated at most times =>

Tree-based UF

• MakeUnionFind(S)
  • Create S trees each containing a single item and size 1 (takes time proportional to the size of S)
• Find(i)
  • Follow the pointer from I to the root of its tree
• Union(x,y)
  • If the size of set x is less than (<) that of y, make x point to y
    • Takes constant time

Runtime of tree-based Find

Find(i) takes time logn in a tree-based union-find data structure containing n items

Proof:

1. the depth of an item equals the number of times the set it was in was renamed
2. The size of the set containing v at least doubles every time the name of the set containing v is changed
3. The largest number of times the size can double is log2n

Option used in UF

1. “Find” operation too much => array based
2. “Union” operation too much => tree based