Priority Queue algo notes

Intro of priority queue

• A data structure that maintains a set of elements S, where each element has associated value key(v) that denotes the priority of element v
• Small keys, higher priority

Resources

https://www.cpp.edu/~ftang/courses/CS241/notes/heap.htm

API

H.insert(i): put item i into heap H

H.deletemin(i): return item with smallest key in H and delete it from H

H.makeheap(S): create a heap from a set of items

H.findmin(): return item with smallest key in H

H.delete(i): remove item I from H

ClosestVertex via heaps

Items: vertices that are on the frontier (incident to the current tree)

Key(v) = distToT[v]

ClosestVertex: return H.deletemin()

Possible implementation

Heap: ordered binary tree

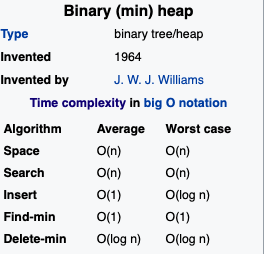
A Binary Heap is a Complete Binary Tree where items are stored in a special order such that the value in a parent node is greater (or smaller) than the values in its two children nodes. The former is called max heap and the latter is called min-heap.

• The heap can be represented by a binary tree or array.

Input data: 4, 10, 3, 5, 1
         4(0)
        /   \
     10(1)   3(2)
    /   \
 5(3)    1(4)

The numbers in bracket represent the indices in the array 
representation of data.

Applying heapify procedure to index 1:
         4(0)
        /   \
    10(1)    3(2)
    /   \
5(3)    1(4)

Applying heapify procedure to index 0:
        10(0)
        /  \
     5(1)  3(2)
    /   \
 4(3)    1(4)
The heapify procedure calls itself recursively to build heap
 in top down manner.

Two constraints

A binary heap is defined as a binary tree with two additional constraints:

• Shape property: a binary heap is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
• Heap property: the key stored in each node is either greater than or equal to (≥) or less than or equal to (≤) the keys in the node’s children, according to some total order.

Heap operations

Both the insert and remove operations modify the heap to conform to the shape property first, by adding or removing from the end of the heap. Then the heap property is restored by traversing up or down the heap. Both operations take O(logn) time

Min heap

1. The keys of the children of u are > the key(u), for all nodes u
2. Along each path keys are monotonically non-decreasing

FindMin

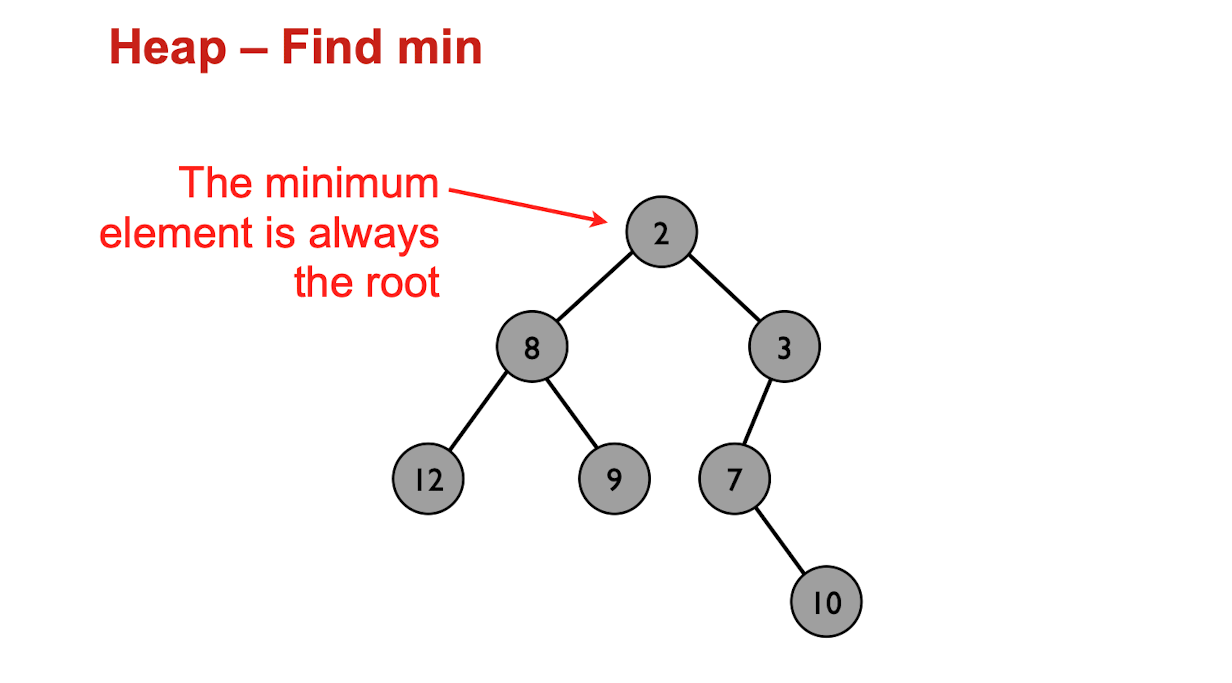
Insert

1. Add node as a leaf
2. “Heapify-up” while current node is <its parent

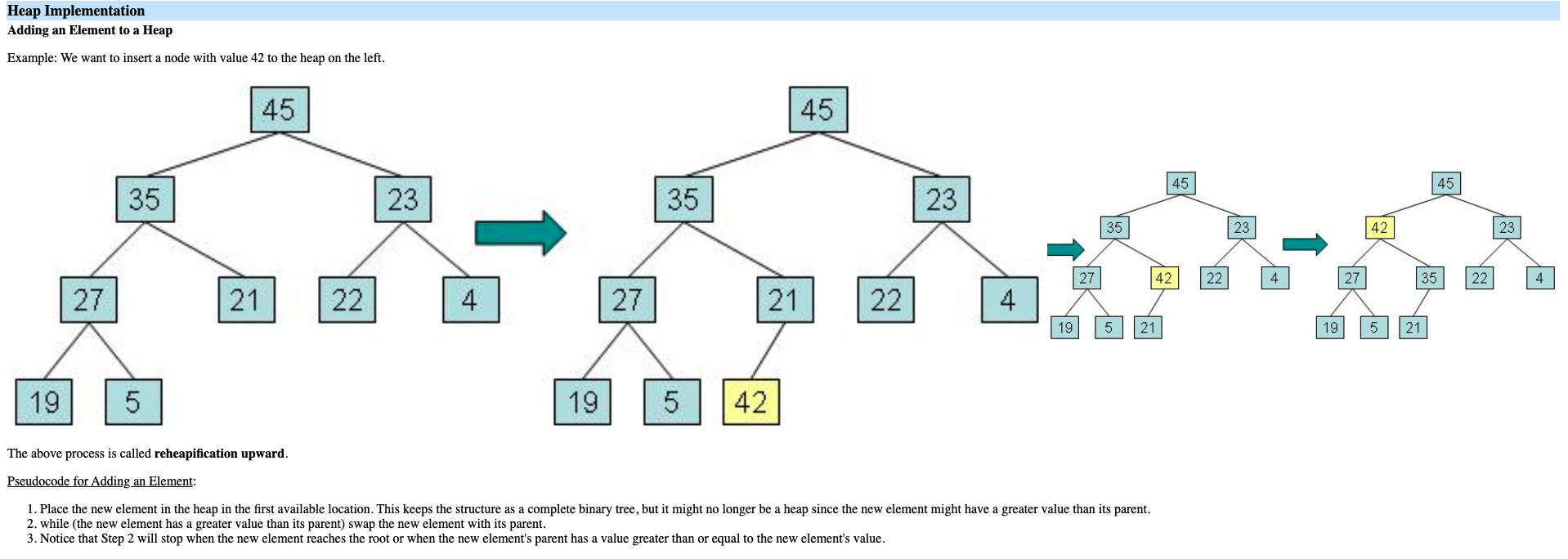
Where to insert?

insert: add the new element as the last element

Delete

1. Need a pointer to node containing key I
2. Replace key to delete I with key j at a leaf node
3. Delete leaf
4. If i>j then sift up, moving j up the tree. If i<j then heaping-down. Swap the current node with smallest of children until its bigger than all of its children.

Where to delete

delete: remove the element and replace it with the last element

Decrease or increase key

The decrease key operation replaces the value of a node with a given value with a lower value, and the increase key operation does the same but with a higher value.

This involves finding the node with the given value, changing the value, and then down-heapifying or up-heapifying to restore the heap property.

Decrease key can be done as follows:

1. Find the index of the element we want to modify
2. Decrease the value of the node
3. Down-heapify (assuming a max heap) to restore the heap property

Increase key can be done as follows:

1. Find the index of the element we want to modify
2. Increase the value of the node
3. Up-heapify (assuming a max heap) to restore the heap property

Running times

• Findmin: take constant time O(1) it is stored in the top
• Insert, delete=> take time proportional to tree height

Heap implementation

A more common approach is to store the heap in an array. Since heap is always a complete binary tree, it can be stored compactly.

No space is required for pointers; instead, the parent and children of each node can be found by simple arithmetic on array indices.

The rules (assume the root is stored in arr[0]):

For each index i, element arr[i] has children at arr[2i + 1] and arr[2i + 2], and the parent at arr[floor( ( i - 1 )/2 )].

This implementation is particularly useful in the heap sort algorithm, where it allows the space in the input array to be reused to store the heap (i.e., the algorithm is in-place). However it requires allocating the array before filling it, which makes this method not that useful in priority queues implementation, where the number of elements is unknown.

It is perfectly acceptable to use a traditional binary tree data structure to implement a binary heap. There is an issue with finding the adjacent element on the last level on the binary heap when adding an element. Here’s a method we can follow.

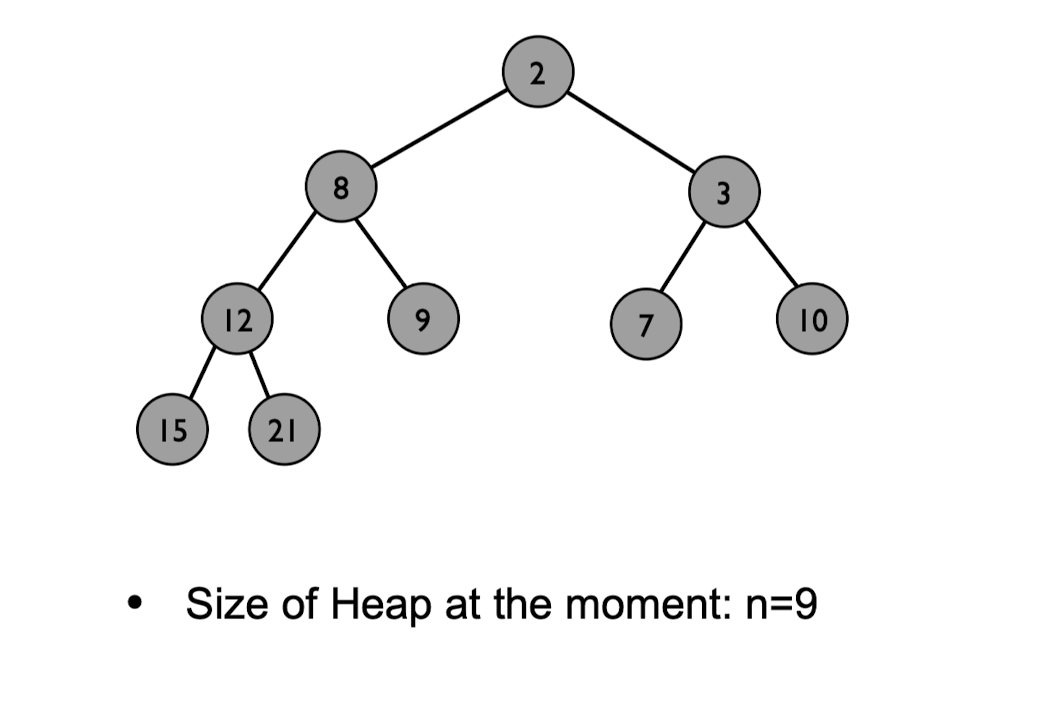
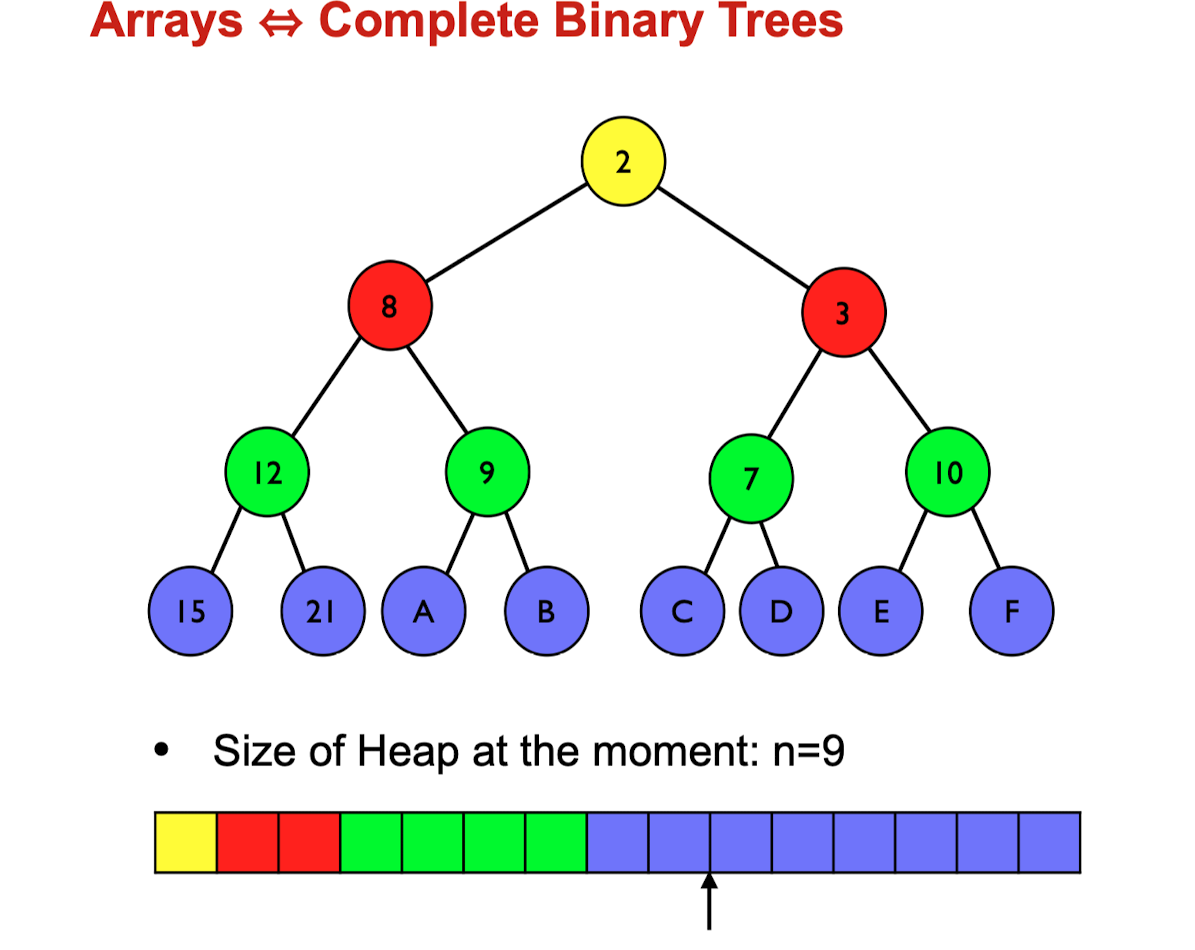
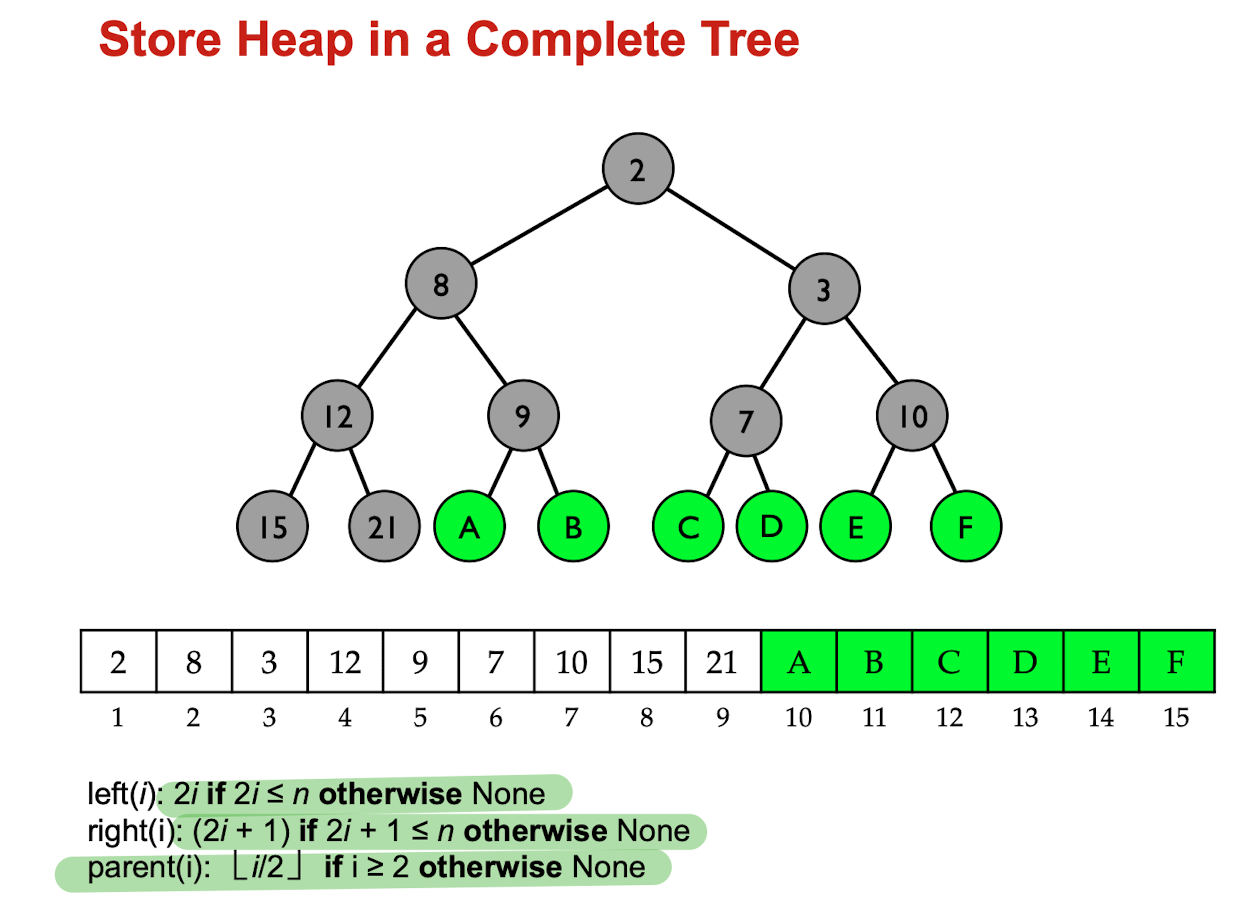
Build a heap

A heap could be built by successive insertions. This approach requires O(n log n) time for n elements, but Williams’ method is suboptimal.

A faster method (due to Floyd) starts by arbitrarily putting the elements on a binary tree, respecting the shape property (the tree could be represented by an array, see below). Then starting from the lowest level and moving upwards, sift the root of each subtree downward as in the deletion algorithm until the heap property is restored.

The optimal method O(N):

• Starts by arbitrarily putting the elements on a binary tree.
• Starting from the lowest level and moving upwards until the heap property is restored by shifting the root of the subtree downward as in the removal algorithm.
• If all the subtrees at some height h (measured from the bottom) have already been “heapified”, the trees at hight h+1 can be heapified by sending their root down. This process takes O(h) swaps.

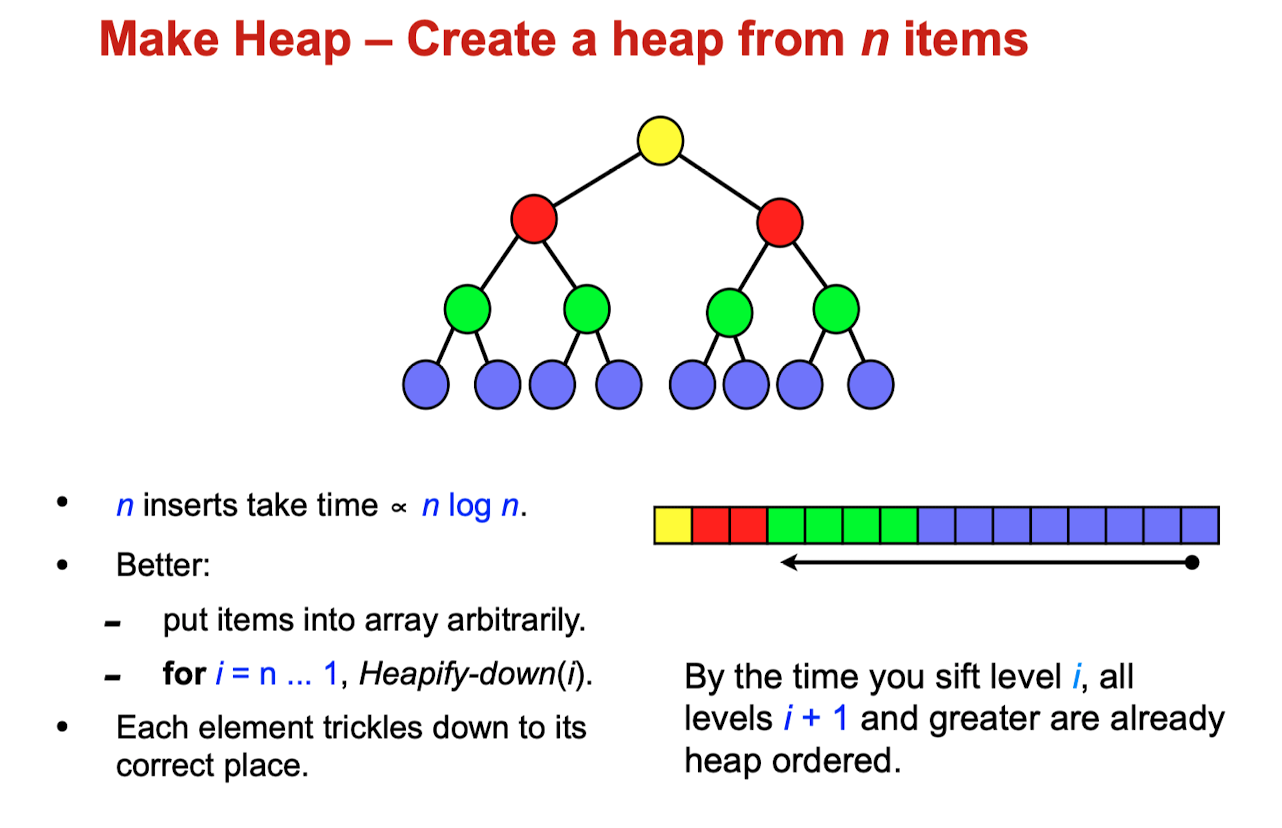
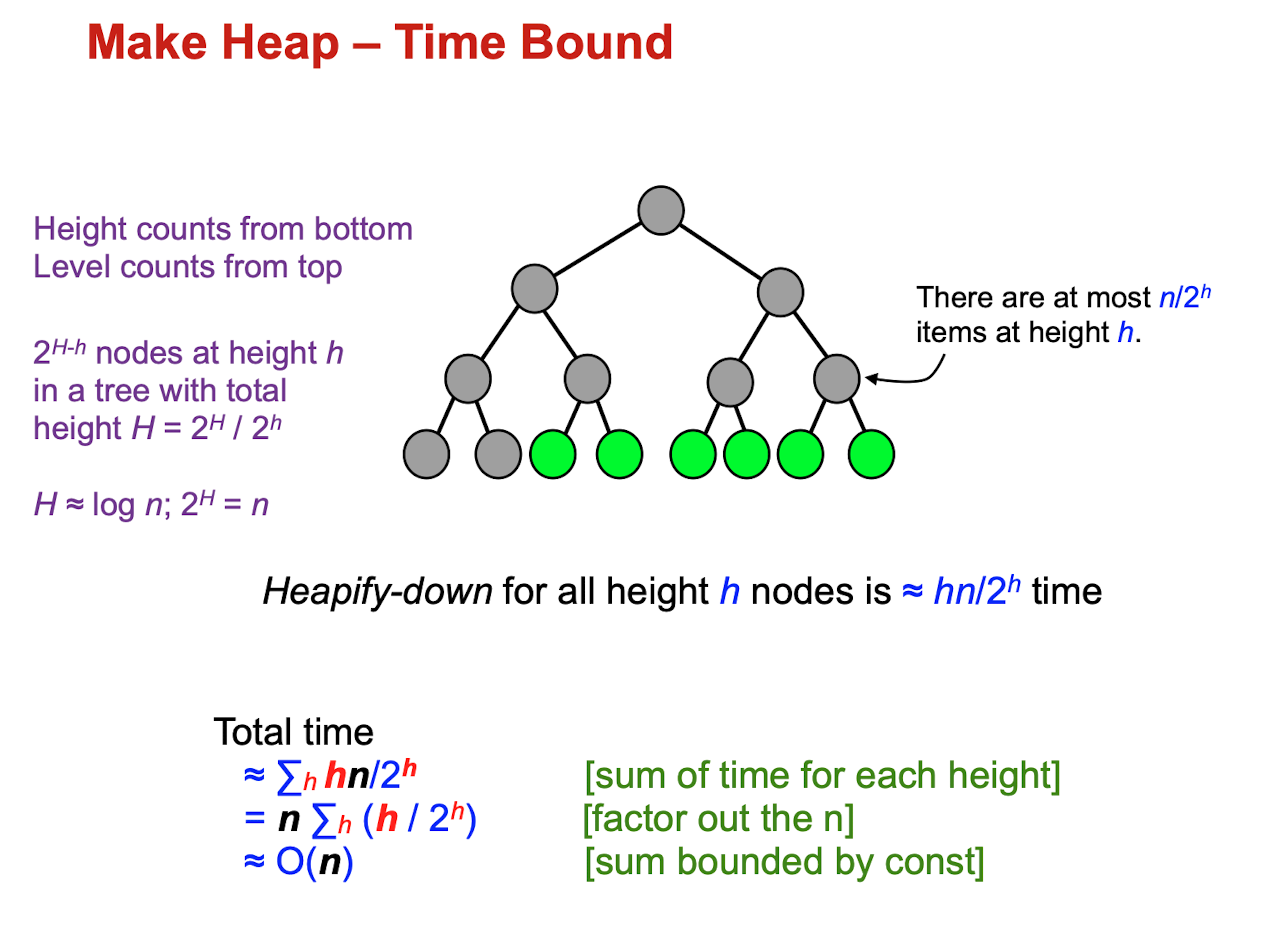
h in this case would be counted from bottom to top.

There are at most items at height h

1. The h layer would contain 1/2 number of the previous layer
2. So n layer would have

Time complexity