MST algo notes

Prior Knowledge

Tree’s characteristics

1. T is a tree
2. T contains no cycles and n-1 edges
3. T is connected and has n-1 edges
4. T is connected and removing any edge disconnects it

MST problem

1. Undirected graph G with vertices for each of n objects
2. Non-negative weights = cost of using edge {u,v}
3. T is connected and has n-1 edges
4. T is connected and removing any edge disconnects it
5. Any two nodes in T are connected by exactly 1 path
6. T is acyclic and adding any new edge creates exactly one cycle.

For the tree MST T, we could obtain

MST property summary

Cut property: The smallest edge crossing any cut must be in all MSTs

Cycle property: the largest edge on any cycle is never in any MST

MST useful statement in HW

1. Let G be a graph where every edge has a different weight. The edge with the smallest edge weight overall is in the minimum spanning tree.

The statement is holding true based on the cut property. Choose the edge e= v,w to be the minimum weight edge in the whole graph where v set S and w V-S. Since e is the minimum weight edge overall, it is also the minimum edge that cross the cut. Therefore, this edge must be in the MST

2. Let G be a graph where every edge has a different weight. There is only one, unique minimum spanning tree in this case

Suppose there is another, different MST D from original tree O. It must contain at least one differing edge d. If this edge is added to the original MST, then a cycle is created where some edge m is the maximum edge. By the cycle property, m can’t belong to any MST. Since m must belong to either D or O which are both MSTs, this leads to a contradiction.

3. Let G be a graph with positive, integer weights where several edges may have the same weights. Show that for integers i, the number of edges of weight i is the same in every MST of G

Suppose not. Let T1 and T2 be two MST that do not have the same number of edges of some weights. Let e be the smallest edge that the 2 MST do not have the same number of it. Suppose T1 has more of it. Then, if we add this e to T2, there should be a cycle made since T2 is a MST. Also, because T1 is a MST, e, which is in T1 cannot be the largest edge in any cycle. Thus there must be an edge in the produced cycle which has a larger weight than e. If we replace it with e, a new spanning tree would made with smaller weights, which would contradict to that T2 is a MST. Thus the number of edges of any weight is the same in every MST of G

Greedy minimum spanning tree rules

Prim’s Algorithm

• Starting with any root node, add the frontier edge with the smallest weight

Kruskal’s Algorithm

• Add edges in increasing weight, skipping those whose addition would create a cycle.

Reverse-Delete algorithm

• Start with all edges, remove them in decreasing order of weight, skipping those whose removal would disconnect the graph

Prims

In this case distToT[u] is a indexMinPriorityQueue, which stores the distance (weight) from u to the MST tree.

• Insert (if neighbor v is not in the MST, insert into the pq)
• Update (neighbor v is in the MST, update the index in pq)

The implementation by priority queue is time complexity wise better, but is really complex as we have implemented our own priority queue. STL provides priority_queue, but the provided priority queue doesn’t support decrease key operation. And in Prim’s algorithm, we need a priority queue and below operations on priority queue :

• ExtractMin : from all those vertices which have not yet been included in MST, we need to get vertex with minimum key value.
• DecreaseKey : After extracting vertex we need to update keys of its adjacent vertices, and if new key is smaller, then update that in data structure.

The algorithm discussed here can be modified so that decrease key is never required. The idea is, not to insert all vertices in priority queue, but only those which are not MST and have been visited through a vertex that has included in MST. We keep track of vertices included in MST in a separate boolean array inMST[].

1) Initialize keys of all vertices as infinite and 
   parent of every vertex as -1.

2) Create an empty priority_queue pq. Every item
   of pq is a pair (weight, vertex). Weight (or 
   key) is used used as first item  of pair
   as first item is by default used to compare
   two pairs.

3) Initialize all vertices as not part of MST yet.
   We use boolean array inMST[] for this purpose.
   This array is required to make sure that an already
   considered vertex is not included in pq again. This
   is where Ptim's implementation differs from Dijkstra.
   In Dijkstr's algorithm, we didn't need this array as
   distances always increase. We require this array here 
   because key value of a processed vertex may decrease
   if not checked.

4) Insert source vertex into pq and make its key as 0.

5) While either pq doesn't become empty 
    a) Extract minimum key vertex from pq. 
       Let the extracted vertex be u.

    b) Include u in MST using inMST[u] = true.

    c) Loop through all adjacent of u and do 
       following for every vertex v.

           // If weight of edge (u,v) is smaller than
           // key of v and v is not already in MST
           If inMST[v] = false && key[v] > weight(u, v)

               (i) Update key of v, i.e., do
                     key[v] = weight(u, v)
               (ii) Insert v into the pq 
               (iv) parent[v] = u
               
6) Print MST edges using parent array.

Java implementation

API

package cn.itcast.algorithm.graph;

import cn.itcast.algorithm.linear.Queue;
import cn.itcast.algorithm.priority.IndexMinPriorityQueue;

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class PrimMST {
    //索引代表顶点，值表示当前顶点和最小生成树之间的最短边
    private Edge[] edgeTo;
    //索引代表顶点，值表示当前顶点和最小生成树之间的最短边的权重
    private double[] distTo;
    //索引代表顶点，如果当前顶点已经在树中，则值为true，否则为false
    private boolean[] marked;
    //存放树中顶点与非树中顶点之间的有效横切边
    private IndexMinPriorityQueue<Double> pq;

    //根据一副加权无向图，创建最小生成树计算对象
    public PrimMST(EdgeWeightedGraph G) {
       //初始化edgeTo
        this.edgeTo = new Edge[G.V()];
        //初始化distTo
        this.distTo = new double[G.V()];
        for (int i = 0; i < distTo.length; i++) {
            distTo[i] = Double.POSITIVE_INFINITY;
        }
        //初始化marked
        this.marked = new boolean[G.V()];
        //初始化pq
        pq = new IndexMinPriorityQueue<Double>(G.V());

        //默认让顶点0进入到树中，但是树中只有一个顶点0，因此，0顶点默认没有和其他的顶点相连，所以让distTo对应位置处的值存储0.0
        distTo[0] = 0.0;
        pq.insert(0,0.0);

        //遍历索引最小优先队列，拿到最小和N切边对应的顶点，把该顶点加入到最小生成树中
        while (!pq.isEmpty()){
            visit(G,pq.delMin());
        }


    }


    //将顶点v添加到最小生成树中，并且更新数据
    private void visit(EdgeWeightedGraph G, int v) {
        //把顶点v添加到最小生成树中
        marked[v] = true;
        //更新数据
        for (Edge e : G.adj(v)) {
            //获取e边的另外一个顶点(当前顶点是v)
            int w = e.other(v);
            //判断另外一个顶点是不是已经在树中，如果在树中，则不做任何处理，如果不再树中，更新数据
            if (marked[w]){
                continue;
            }


            //判断边e的权重是否小于从w顶点到树中已经存在的最小边的权重；
            if (e.weight()<distTo[w]){
                //更新数据
                edgeTo[w] = e;

                distTo[w] = e.weight();

                // 如果w已经在pq中存在，则update w的值为e.weight
                if (pq.contains(w)){
                    pq.changeItem(w,e.weight());
                }else{
                    pq.insert(w,e.weight());
                }

            }


        }

    }

    //获取最小生成树的所有边
    public Queue<Edge> edges() {
        //创建队列对象
        Queue<Edge> allEdges = new Queue<>();
        //遍历edgeTo数组，拿到每一条边，如果不为null，则添加到队列中
        for (int i = 0; i < edgeTo.length; i++) {
            if (edgeTo[i]!=null){
                allEdges.enqueue(edgeTo[i]);
            }
        }
        return allEdges;
    }


}

Time complexity

Because each vertex is inserted in the priority queue only once and insertion in priority queue take logarithmic time.

Kruskal’s algorithm

array based UF:

1. Sort the edges mlogm for m edges (), could be rewritten as mlogn
2. 2m “find” operations check wheter u and v are in the same component
3. At most n-1 union operations nlogn time (UF notes)

Total running time would be mlogn + 2m + nlogn

tree based UF:

1. Sorting the edges: mlogn
2. At most 2m “find” operations logn time each
3. At most n-1 union operations: n items

Total running time would be mlogn + 2mlogn + n

Option used in UF

1. “Find” operation too much => array based
2. “Union” operation too much => tree based

Clustering - Kruskal’s algorithm application

Also known as the Maximum Minimum Distance

Goal: divide the n items up into k groups so that the minimum distance between items in different group is maximized

Idea

• Maintain clusters as a set of connected components of a graph
• Iteratively combine the clusters containing the two closest items
• Stop when there are two clusters

This is exactly Kruskal’s algorithm

1. The clusters are the connected components that Kruskal’s algorithm has created after a certain point
2. Example of single-link, agglomerative clustering

Agglomerative: combine clusters single-link: combine as soon as a single link joins clusters.

Another way

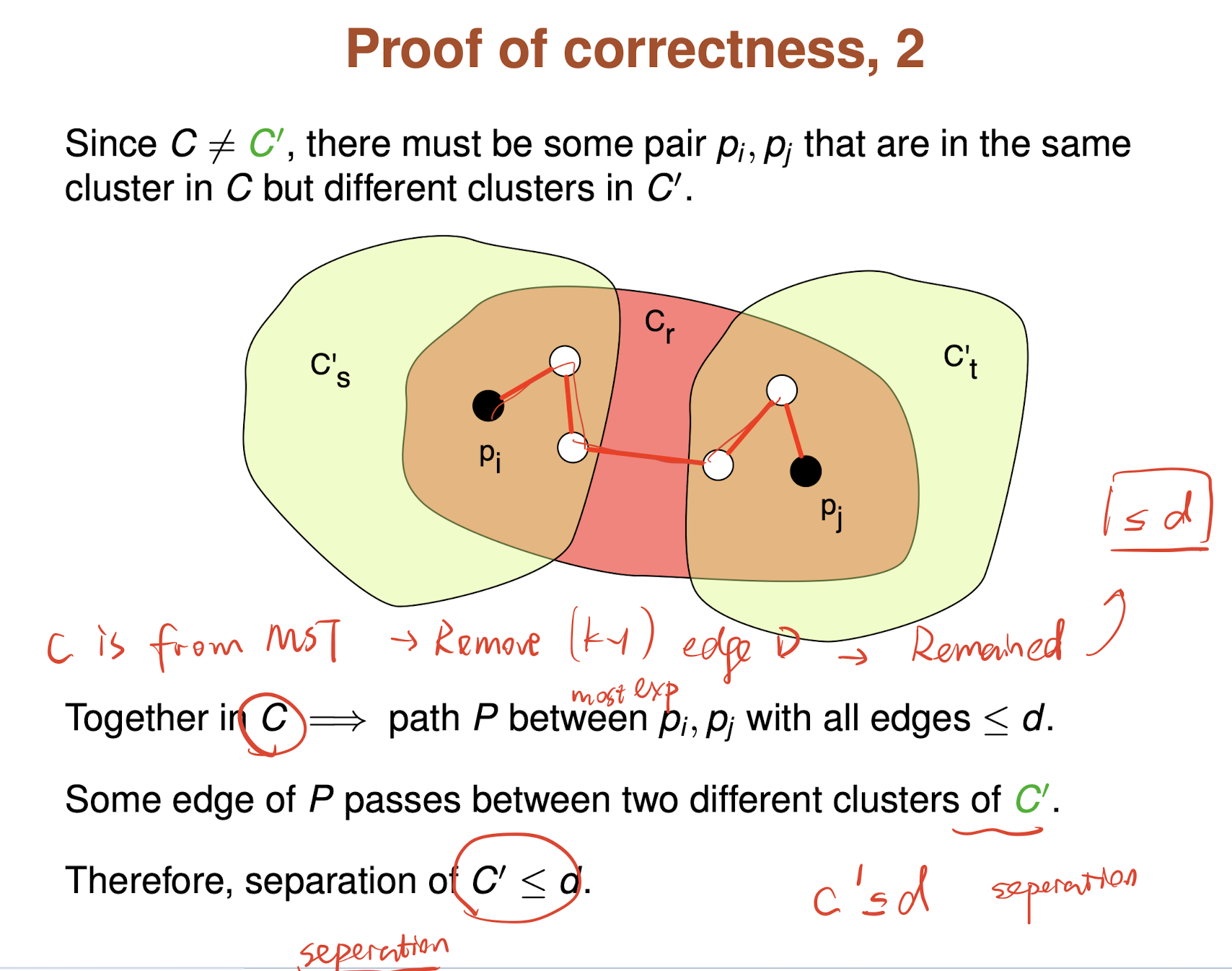
Delete the k-1 most expensive edges from the MST.

The spacing d of the clustering C that this produces is the length of the (k-1)st most expensive edge

Negative weight for MST

The concept of MST allows weights of an arbitrary sign. The two most popular algorithms for finding MST (Kruskal’s and Prim’s) work fine with negative edges.

Actually, you can just add a big positive constant to all the edges of your graph, making all the edges positive. The MST (as a subset of edges) will remain the same.