Cut Property in MST

5. Cut Property in Minimum Spanning Tree

5.1. Statement

Now we know that a cut splits the vertex set of a graph into two or more sets. A cut set contains a set of edges whose one endpoint is in one graph and the other endpoint is in another graph. When constructing a minimum spanning tree (MST), the original graph should be a weighted and connected graph. Let’s assume that all edges cost in the MST is distinct.

According to the cut property, if there is an edge in the cut set which has the smallest edge weight or cost among all other edges in the cut set, the edge should be included in the minimum spanning tree.

5.2. Example

We’re taking a weighted connected graph here:

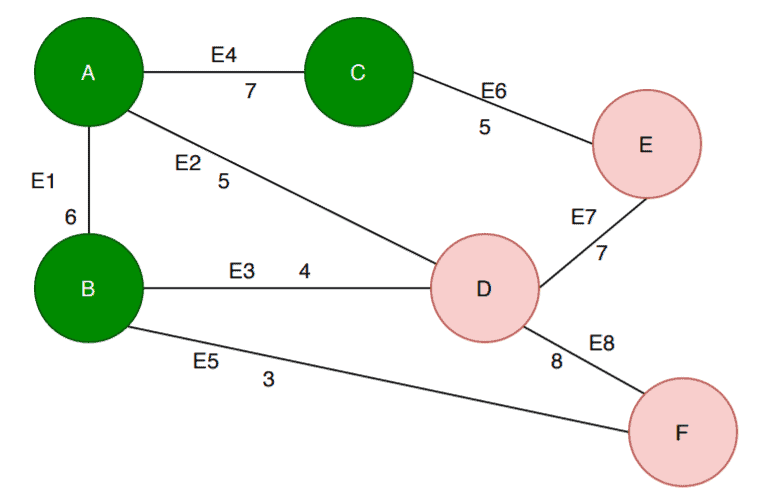
In this example, a cut divided the graph into two subgraphs S_1 (green vertices) and S_2 (pink vertices). The cut set for would be (E2, E3, E5, E6) . Now according to the cut property, the minimum weighted edge from the cut set should be present in the minimum spanning tree of . Here the minimum weighted edge from the cut set is .

Now we’ll construct a minimum spanning tree of and check weather the edge is present or not:

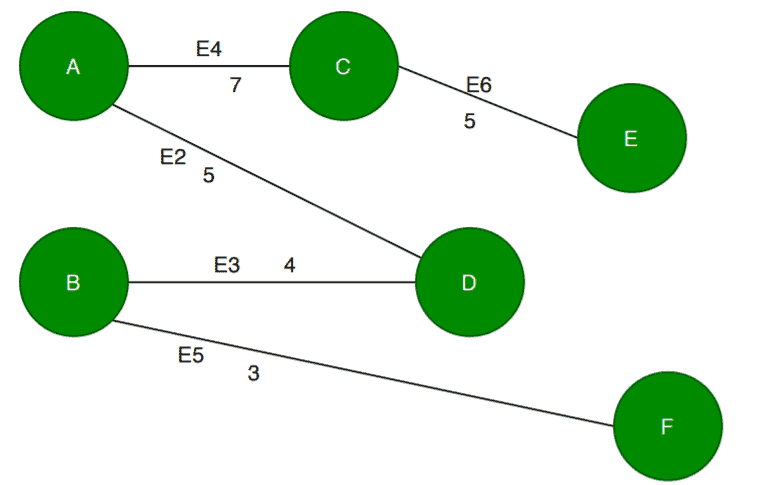
This is one of the minimum spanning trees of , and as we can see, the edge is present here. So we can say the cut property works fine for the graph .

What about other graphs? Will the cut property holds for all other minimum spanning trees? Let’s find out in the next section.

5.3. Proof of Cut Property

Now to conclude that the cut property will work for all the minimum spanning tree, we’re presenting a formal proof in this section.

Let’s assume that we build a minimum spanning tree from a graph . We also defined a cut which split the vertex set into two sets and . Furthermore, we assume that there exists an edge E_C joining two sets , , and has the smallest weight.

Now we’re starting this proof by assuming the edge $\mathbf{E_C}$ is not a part of the MST $\mathbf{T}$ . It would be interesting here to see what happens if we include E_C to the MST . If we include E_C in , it’ll create a cycle. But according to the definition of MST, a cycle can’t be part of MST.

Now, if we analyze the MST , there must be some edge in , let’s name it as , other than E_C which has one endpoint in and another endpoint in . Now initially, we assumed that E_C has the smallest weight among all the edges which joins and . This implies that the edge $\mathbf{K}$ must be of higher weight than $\mathbf{E_C}$ .

Therefore is a spanning tree but not a minimum spanning tree. If we include the edge E_C and then construct the MST, the total weight of the MST would be less than the previous one. Also, can’t contain both E_C and as it will create a cycle. Therefore our initial assumption that E_C is not a part of the MST should be wrong.

Hence we can conclude that the minimum weighted edge in the cut set should be part of the minimum spanning tree of that graph.

Let’s simplify the proof with an example:

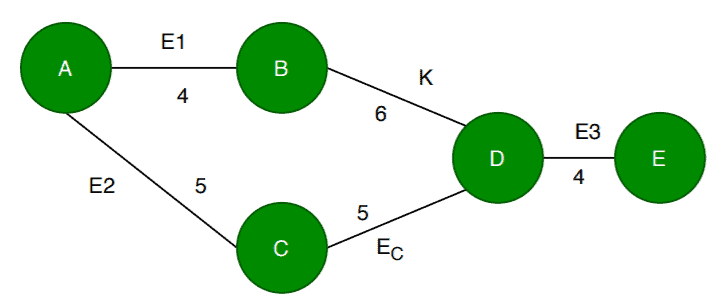
We’re taking a connected weighted graph . Now let’s define a cut of :

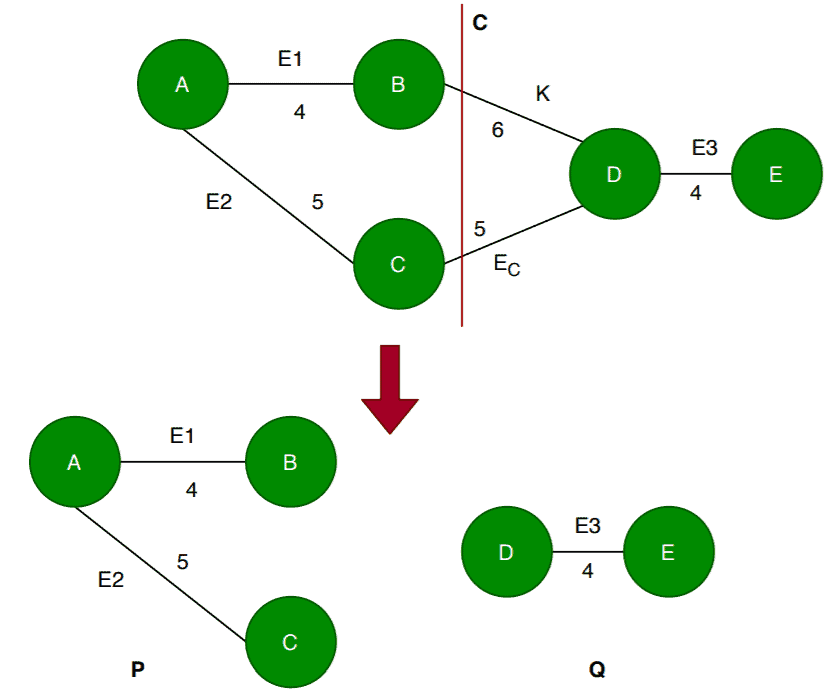
The cut divided the graph into two subgraphs and . Now there are two edges that connect and among which E_C is the minimum weighted edge. First, we’ll construct a minimum spanning tree from without including the edge E_C :

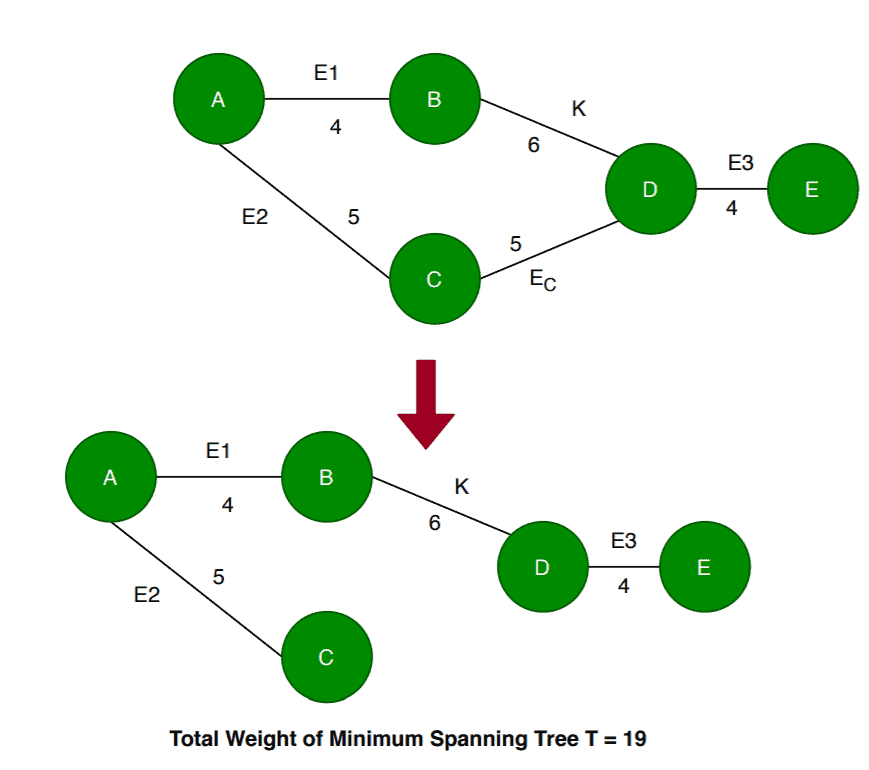
The total weight of the minimum spanning tree here is . Previously we defined that E_C is the minimum weighted edge in the cut set. It means the weight of the edge should be greater than the edge E_C . In such a case, the currently constructed spanning tree is not an MST as we can build a spanning tree which can be less weighted than the current one:

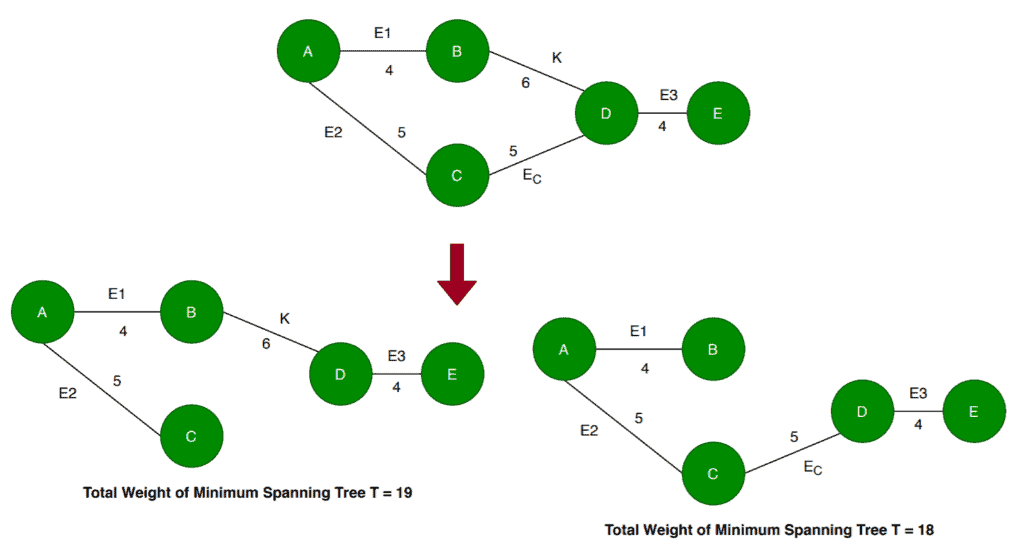
As we can see, when we include the edge in the spanning tree, the total weight of the spanning tree would become which is higher than the weight when we construct by including the edge E_C . Therefore if we include the edge $\mathbf{K}$ , then it won’t be a minimum spanning tree.

Hence, we proved that the minimum spanning tree corresponds to a connected weighted graph should include the minimum weighted edge of the cut set.