DFS and BFS algo notes

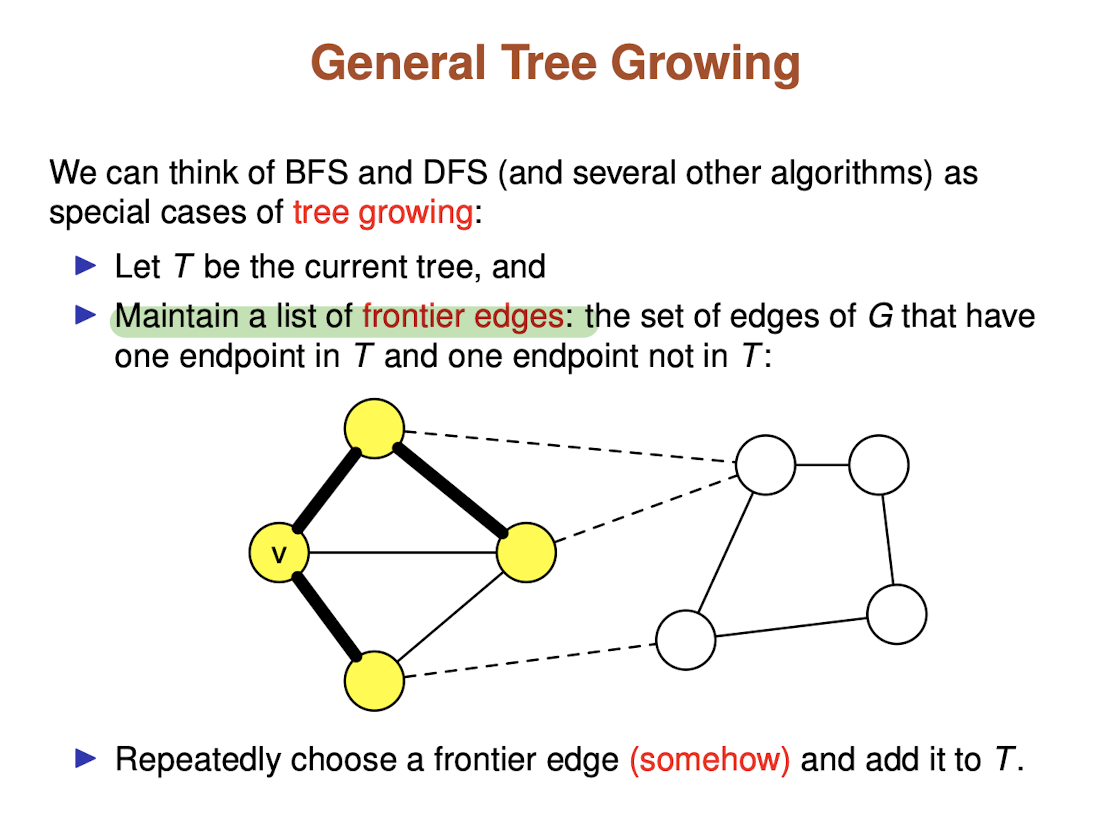
General Tree growing

• Let T be the current tree
• Maintain a list of frontier edges : the set of edges of F that have one endpoint in T and one endpoint not in T
• Repeatedly choose a frontier edge (somehow) and add it to T

Implementation of tree growing

1. DFS
2. BFS
3. Prim’s algorithms
4. Dijkstra’s shortest path
5. A*

BFS & DFS as Tree Growing

1. nextEdge() for DFS:
   • Select a frontier edge whose tree endpoint was discovered most recently (Stack)
   • Run time for DFS: O(E)
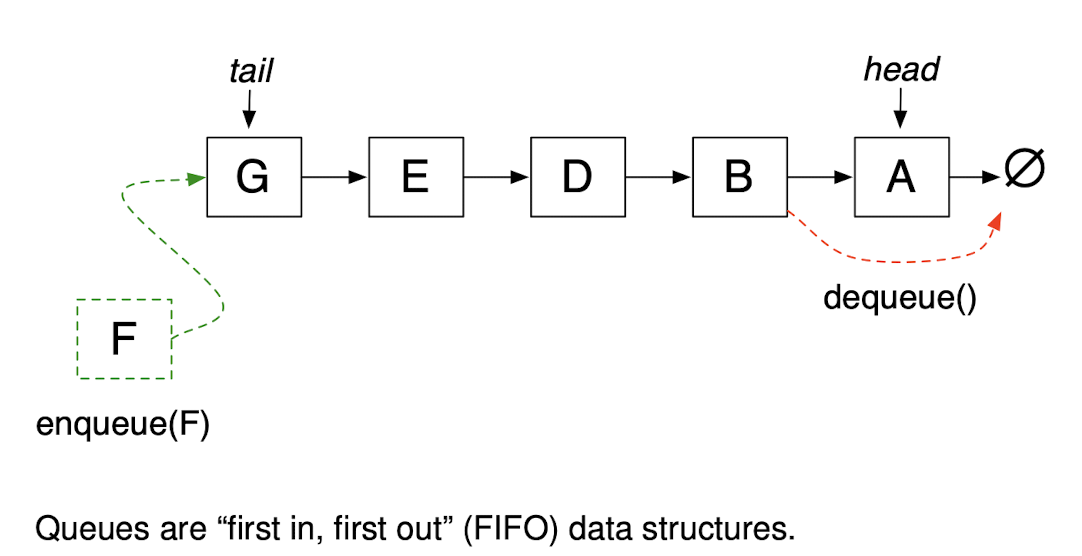
2. nextEdge()for BFS
   • Select a frontier edge whose tree endpoint was discovered least recently (Queue)
   • Run time for BFS: O(E)

nextEdge for BFS

nextEdge: frontier edge connecting to node with earliest discovery time

A queue maintains a list of items in order of their discovery so that the item discovered farthest in the past can be accessed quickly

procedure bfs(G,root) is
	let Q be a queue 
	mark root as explored
	Q.enqueue(root)
	while Q is not empty do
		v:= Q.dequeue
		if v is the goal then return v
		for all edges from v to w in G.adjacnetEdges(v) do 
			if w is not marked then label w as explored
				Q.enqueue(w)

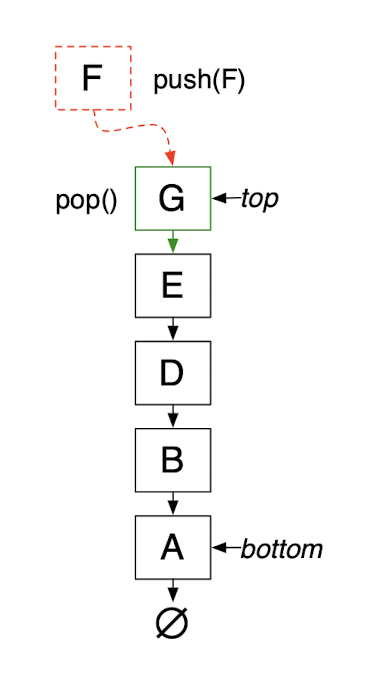
nextEdge for DFS

nextEdge: frontier edge connecting to node with latest discovery time

A stack maintains a list of items so they can be accessed in reverse order of their discovery times

A stack is a “last in, first out” (LIFO) data structure

procedure DFS(G,s)
	S:= stack containing only s
	S.push(s)
	while s not empty
		v:= s.pop()
		if v is not visited:
			mark v as visited
			for w in G.neighbors(v):
				s.push(w)

Recursion based implementation

procedure dfs (G,u)
	mark u as visited
	while u has an unvisited neighbor in G
		v:= an unvisited neighbor of u
		dfs(G,u)

DFS

Basic idea

• DFS keeps walking down a path until it forced to backtrack

• It backtrack until find a new path to go down

• The overall results would be a DFS tree

• LIFO (Last IN First OUT Method)

Non-DFS-Tree edges

Theorem: Let x and y be nodes in the DFS tree such that {x,y} is an edge in a undirected graph G. Then one of x or y is an ancestor of the other in

Recursive implementation of DFS

Algorithm

1. Create a recursive function that takes the index of the node and a visited array
2. Mark the current node/vertex as visited and print the node (this would be further code processing part)
3. Traverse all the adjacency and mark all the nodes and recursively use the dfs functions

pseudo code

procedure dfs (G,u)
	mark u as visited
	while u has an unvisited neighbor in G
		v:= an unvisited neighbor of u
		dfs(G,u)

Java implementation

package graph;

public class DFS {
    public boolean[] visited;
    private int count;

    // creat the DFS object
    public DFS(Graph G, int s) {
        visited = new boolean[G.V()];
        dfs(G, s);
    }

    // use DFS to find all the adjacent point in graph G
    public void dfs(Graph g, int v) {
        // mark vertex v as visited
        visited[v] = true;
      	// print the vertex v, if further process needs, type code in this place
        System.out.println(v);

        // Iterate through all the neighbor, obtain each vertex w
        for (Integer w : g.adj(v)) {
            if (!visited[w]) dfs(g, w);
        }
        count++;
    }

    // check whether w and s are connected
    public boolean visited(int w) {
        return visited[w];
    }

    // obtain the number of vertex that is connected to vertex s
    public int count() {
        return count;
    }

}

Stack based implantation of DFS

procedure DFS(G,s)
	S:= stack containing only s
	S.push(s)
	while s not empty
		v:= s.pop()
		if v is not visited:
			mark v as visited
			for w in G.neighbors(v):
				s.push(w)

package graph;

import java.util.Stack;

public class DFS_Stack {
    public boolean[] visited;

    public DFS_Stack(Graph g, int s) {
        visited = new boolean[g.V()];
        for (int i = 0; i < g.V(); i++) {
            if (!visited[i]) dfs(g, s);
        }
    }

    public void dfs(Graph g, int s) {
        // create a stack used to do iterative DFS
        Stack<Integer> stack = new Stack<>();

        // push the source node into stack
        stack.push(s);

        // while s not empty
        while (!stack.empty()) {
            // pop a vertex from the
            int v = stack.pop();

            // if the vertex v is already visited, we would ignore it
            if (visited[v]) continue;

            // the vertex v is not yet visited, we would mark as true
            visited[v] = true;
            System.out.println(v);

            // do for every edge v->w

            for (Integer w : g.adj(v)) {
                if (!visited[w]) {
                    stack.push(w);
                }

            }

        }
    }
}

Comparison of recursively achieved and stack-based algorithm

These two variations of DFS visit the neighbors of each vertex in the opposite order from each other: the first neighbor of v visited by the recursive variation is the first one in the list of adjacent edges, while in the iterative variation the first visited neighbor is the last one in the list of adjacent edges.

The recursive implementation will visit the nodes from the example graph in the following order: A, B, D, F, E, C, G.

The non-recursive implementation will visit the nodes as: A, E, F, B, D, C, G.

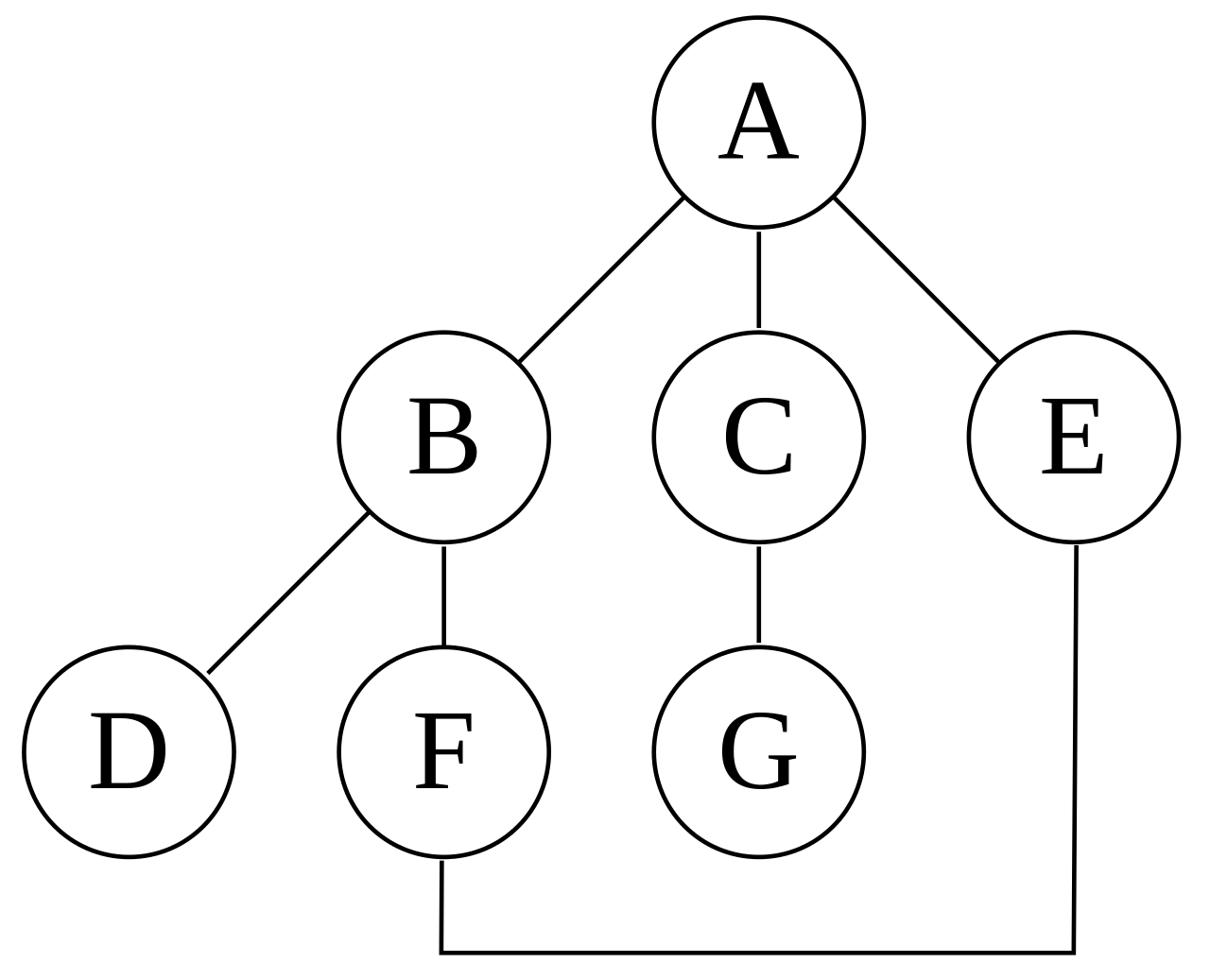
The non-recursive implementation is similar to breadth-first search but differs from it in two ways:

1. it uses a stack instead of a queue, and
2. it delays checking whether a vertex has been discovered until the vertex is popped from the stack rather than making this check before adding the vertex.

If G is a tree, replacing the queue of the breadth-first search algorithm with a stack will yield a depth-first search algorithm. For general graphs, replacing the stack of the iterative depth-first search implementation with a queue would also produce a breadth-first search algorithm, although a somewhat nonstandard one.[7]

Another possible implementation of iterative depth-first search uses a stack of iterators of the list of neighbors of a node, instead of a stack of nodes. This yields the same traversal as recursive DFS.[8]

Topological sorting (DFS application)

DAGs

A directed, acyclic graph (DAG) is a graph that contains no directed cycles. (After leaving any node u can never get back to u by following edges along the arrows)

DAGs are very useful in modeling project dependencies: Task i has to be done before task j and k which have to be done before m

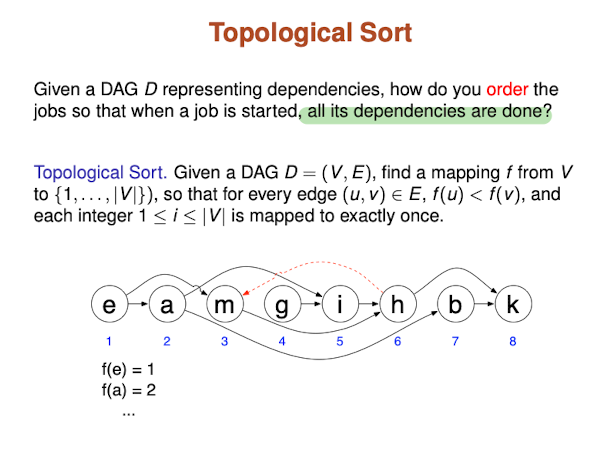
Theorem:

1. Every DAG contains a vertex with no incoming edges.

2. If a directed graph G is a DAF, then G has a topological ordering. Also, if a directed graph G has a topological ordering, then G is a DAG.

Being a DAG <=> having a topological ordering, because a topological ordering implies that there are no cycles in the directed graph.

Topological sorting algorithm

Topological sort:

1. Let i = 1
2. Find a node u with no incoming edges, and let f(u) = i
3. Delete u from the graph
4. Increment I

Implementation: Maintain

1. Income[w] = number of incoming edges for node w
2. A list S of nodes that currently have no incoming edges

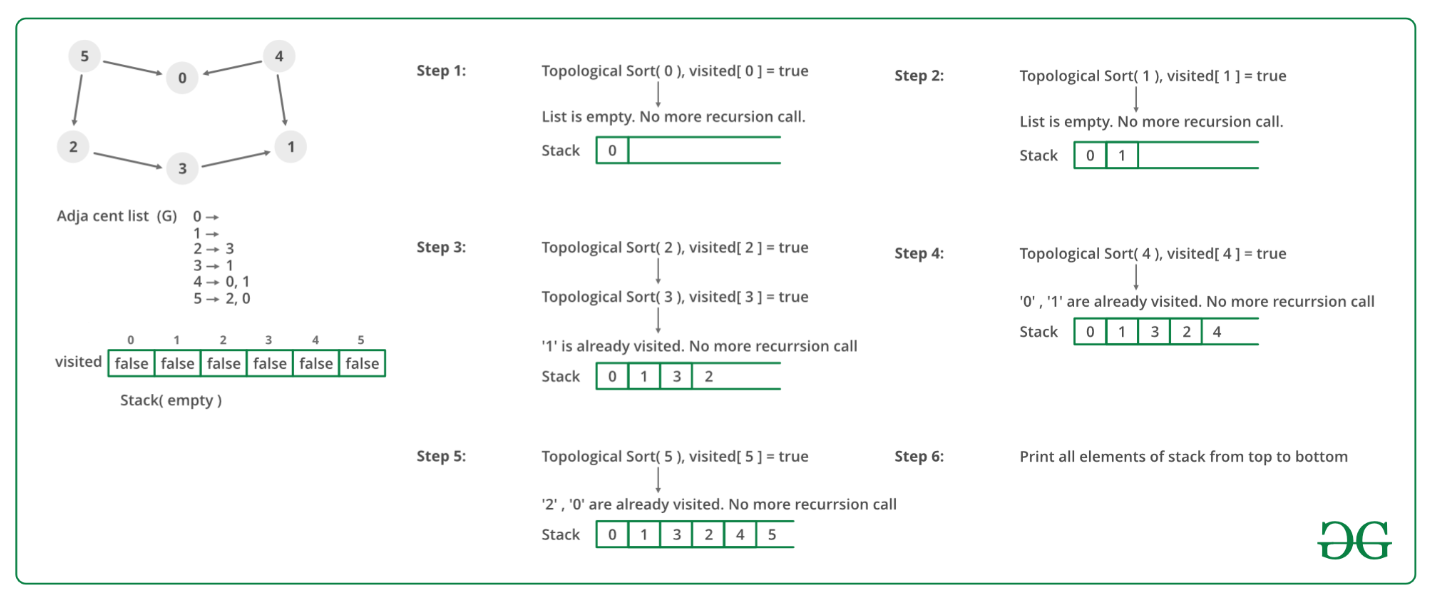
When we delete a node u, we decrement Income[w] for all neighbors w of u. If Income[w] becomes 0, we add w to S.

Topological sorting

package cn.itcast.algorithm.graph;

import cn.itcast.algorithm.linear.Stack;

public class TopoLogical {
    //顶点的拓扑排序
    private Stack<Integer> order;

    //构造拓扑排序对象
    public TopoLogical(Digraph G) {
        //创建一个检测有向环的对象
        DirectedCycle cycle = new DirectedCycle(G);
        //判断G图中有没有环，如果没有环，则进行顶点排序：创建一个顶点排序对象
        if (!cycle.hasCycle()){
            DepthFirstOrder depthFirstOrder = new DepthFirstOrder(G);
            order = depthFirstOrder.reversePost();
        }
    }

    //判断图G是否有环
    private boolean isCycle(){
        return order==null;
    }

    //获取拓扑排序的所有顶点
    public Stack<Integer>  order(){
        return order;
    }
}

DepthFirstOrder

package cn.itcast.algorithm.graph;

import cn.itcast.algorithm.linear.Stack;

public class DepthFirstOrder {
    //索引代表顶点，值表示当前顶点是否已经被搜索
    private boolean[] marked;
    //使用栈，存储顶点序列
    private Stack<Integer> reversePost;

    //创建一个检测环对象，检测图G中是否有环
    public DepthFirstOrder(Digraph G){
        //初始化marked数组
        this.marked = new boolean[G.V()];
        //初始化reversePost栈
        this.reversePost = new Stack<Integer>();

        //遍历图中的每一个顶点，让每个顶点作为入口，完成一次深度优先搜索
        for (int v = 0;v<G.V();v++){
            if (!marked[v]){
                dfs(G,v);
            }
        }
    }

    //基于深度优先搜索，把顶点排序
    private void dfs(Digraph G, int v){
        //标记当前v已经被搜索
        marked[v] = true;
        //通过循环深度搜索顶点v
        for (Integer w : G.adj(v)) {
            //如果当前顶点w没有搜索，则递归调用dfs进行搜索
            if (!marked[w]){
                dfs(G,w);
            }
        }
        //让顶点v进栈
        reversePost.push(v);
    }

    //获取顶点线性序列
    public Stack<Integer>  reversePost(){
        return reversePost;
    }
}

DirectedCycle

package cn.itcast.algorithm.graph;

public class DirectedCycle {
    //索引代表顶点，值表示当前顶点是否已经被搜索
    private boolean[] marked;
    //记录图中是否有环
    private boolean hasCycle;
    //索引代表顶点，使用栈的思想，记录当前顶点有没有已经处于正在搜索的有向路径上
    private boolean[] onStack;

    //创建一个检测环对象，检测图G中是否有环
    public DirectedCycle(Digraph G){
        //初始化marked数组
        this.marked = new boolean[G.V()];
        //初始化hasCycle
        this.hasCycle = false;
        //初始化onStack数组
        this.onStack = new boolean[G.V()];

        //找到图中每一个顶点，让每一个顶点作为入口，调用一次dfs进行搜索
        for (int v =0; v<G.V();v++){
            //判断如果当前顶点还没有搜索过，则调用dfs进行搜索
            if (!marked[v]){
                dfs(G,v);
            }

        }


    }

    //基于深度优先搜索，检测图G中是否有环
    private void dfs(Digraph G, int v){
        //把顶点v表示为已搜索
        marked[v] = true;

        //把当前顶点进栈
        onStack[v] = true;

        //进行深度搜索
        for (Integer w : G.adj(v)) {
            //判断如果当前顶点w没有被搜索过，则继续递归调用dfs方法完成深度优先搜索
            if (!marked[w]){
                dfs(G,w);
            }

            //判断当前顶点w是否已经在栈中，如果已经在栈中，证明当前顶点之前处于正在搜索的状态，那么现在又要搜索一次，证明检测到环了
            if (onStack[w]){
                hasCycle = true;
                return;
            }
        }
        //把当前顶点出栈
        onStack[v] = false;
    }

    //判断当前有向图G中是否有环
    public boolean hasCycle(){
        return hasCycle;
    }

}

Run time analysis

Applications

Design an algorithm to determine whether a DAG has a unique topological ordering

We would firstly run a topological sort on G, since this is a DAG. Denote this order as L, we then check whether there is an edge going from first node in L to the second node in L. Similarly check the edge from second to third. Repeatedly check all the vertices. If all of the vertices follow the previous rules, then return true, it has a unique topological ordering, otherwise, return false.

BFS

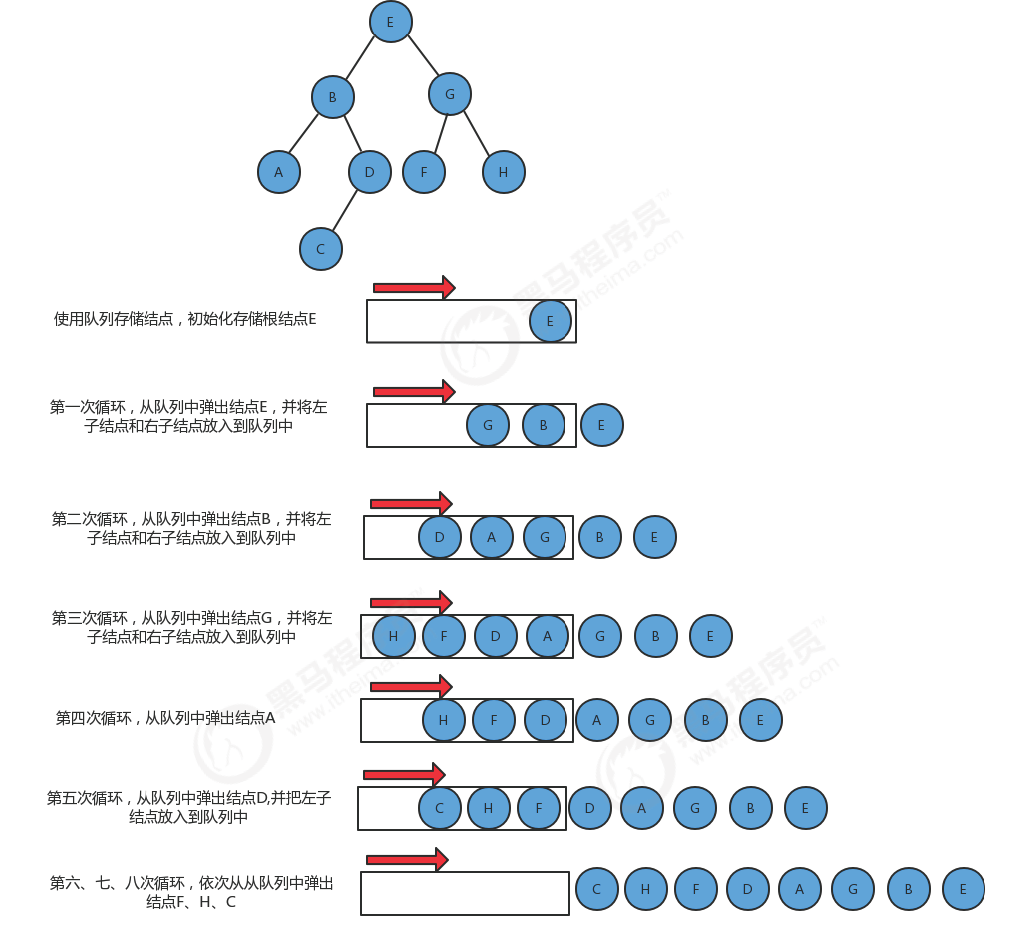
Pseudocode

procedure bfs(G,root) is
	let Q be a queue 
	mark root as explored
	Q.enqueue(root)
	while Q is not empty do
		v:= Q.dequeue
		if v is the goal then return v
		for all edges from v to w in G.adjacnetEdges(v) do 
			if w is not marked then label w as explored
				Q.enqueue(w)

Java implementation

package graph;

import java.util.LinkedList;
import java.util.Queue;

public class BFS {
    public boolean[] marked;
    private int count;

    private Queue<Integer> waitSearch;

    public BFS(Graph G, int s) {
        this.marked = new boolean[G.V()];
        this.count = 0;
        this.waitSearch = new LinkedList<>();
        bfs(G,s);
    }

    private void bfs(Graph G, int v) {
        // mark v as visited
        marked[v] = true;

        // let v in the queue, ready to search
        waitSearch.add(v);

        System.out.println(v);

        while (!waitSearch.isEmpty()) {
            Integer wait = waitSearch.remove();
            // iterate wait's adjacency matrix
            for (Integer w : G.adj(wait)) {
                if (!marked[w]) {
                    marked[w] = true;
                    waitSearch.add(w);
                    System.out.println(w);
                }

            }
        }

        // let connected vertex +1
        count++;
    }

    public boolean marked(int w) {
        return marked[w];
    }

    public int count() {
        return count;
    }
}

Finding all connected components

Bipartiteness

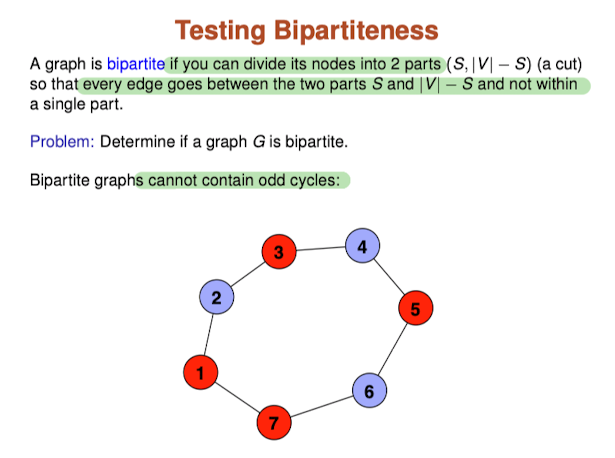
Solution:

1. Do a BFS starting from some node s
2. Color even levels “blue” and odd levels “red”
3. Check each edge to see if any edge has both endpoints the same level

Notice:

Nodes in adjacent levels must get different colors because by construction there are edges between adjacent levels

Proof of Correctness for Bipartite Testing

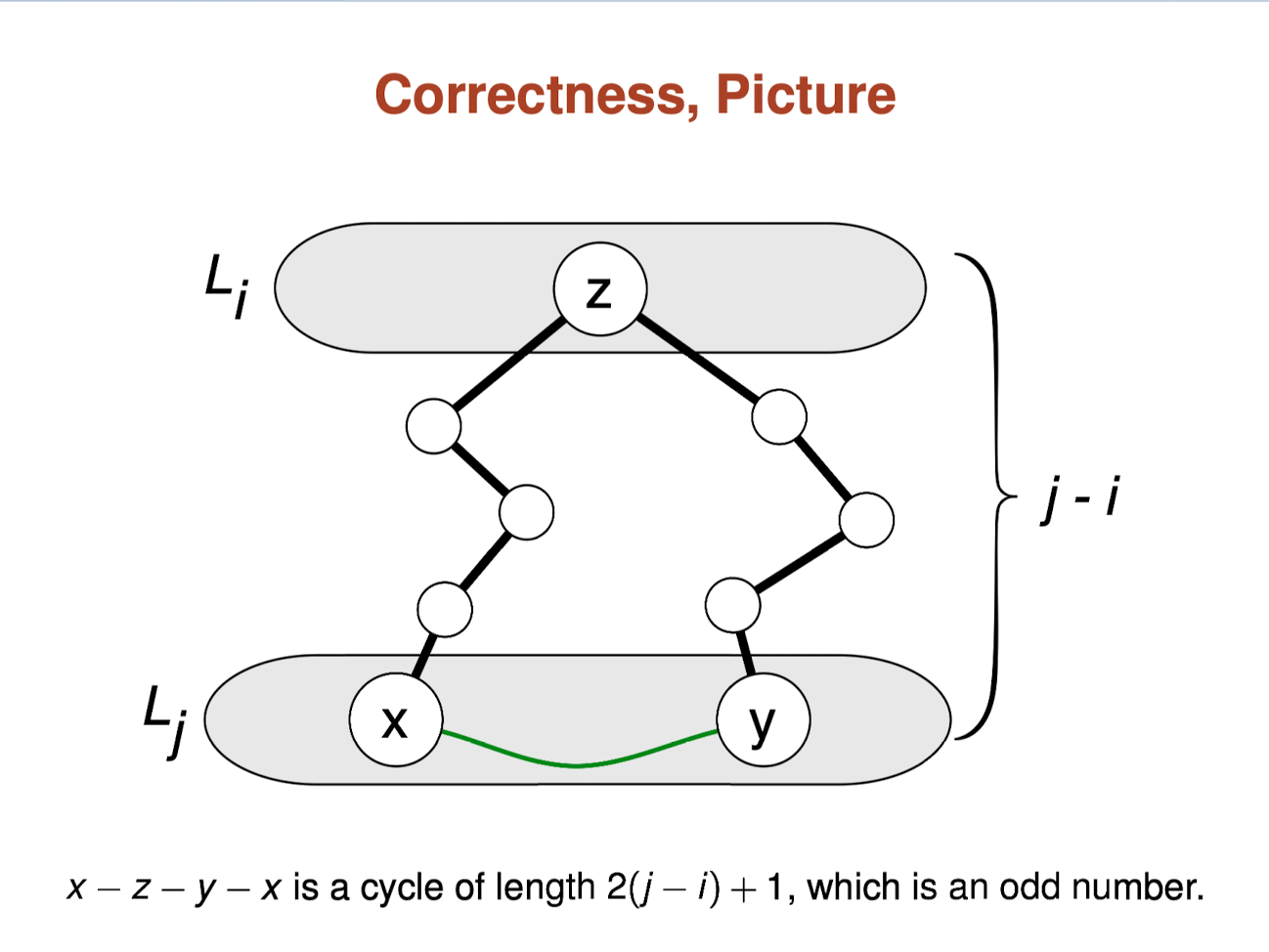
Bipartite Graph Checker

We can use the O(V+E) DFS or BFS (they work similarly) to check if a given graph is a Bipartite Graph by giving alternating color (orange versus blue in this visualization) between neighboring vertices and report ‘non bipartite’ if we ends up assigning same color to two adjacent vertices or ‘bipartite’ if it is possible to do such ‘2-coloring’ process. Try DFS_Checker or BFS_Checker on the example Bipartite Graph.

Bipartite Graphs have useful applications in (Bipartite) Graph Matching problem.

Note that Bipartite Graphs are usually only defined for undirected graphs so this visualization will convert directed input graphs into its undirected version automatically before continuing. This action is irreversible and you may have to redraw the directed input graph again for other purposes.

Applications

Detecting cycle

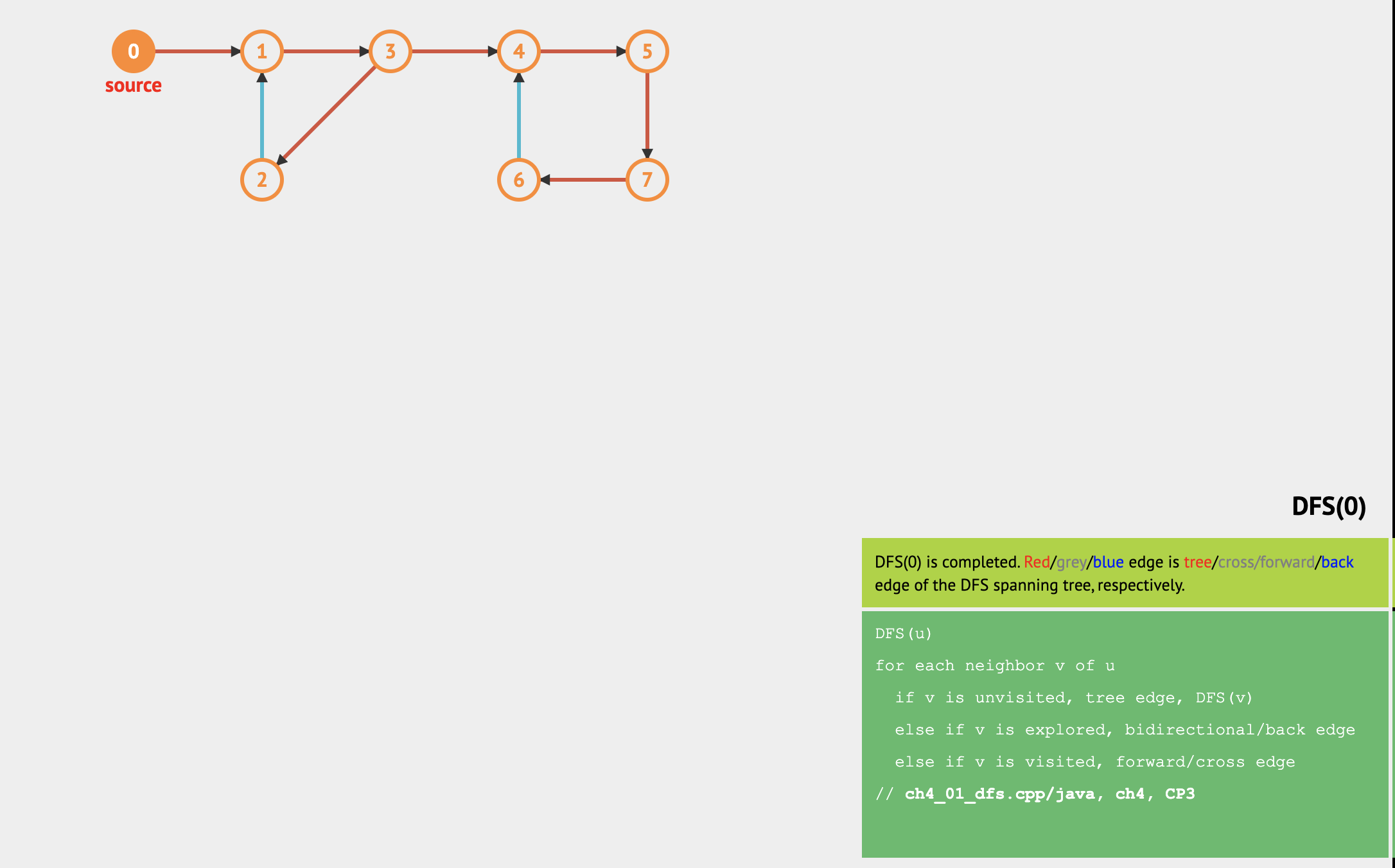
We can actually augment the basic DFS further to give more insights about the underlying graph.

In this visualization, we use blue color to highlight back edge(s) of the DFS spanning tree. The presence of at least one back edge shows that the traversed graph (component) is cyclic while its absence shows that at least the component connected to the source vertex of the traversed graph is acyclic.

Back edge can be detected by modifying array status[u] to record three different states:

1. unvisited: same as earlier, DFS has not reach vertex u before,
2. explored: DFS has visited vertex u, but at least one neighbor of vertex u has not been visited yet (DFS will go depth-first to that neighbor first),
3. visited: now stronger definition: all neighbors of vertex u have also been visited and DFS is about to backtrack from vertex u to vertex p[u].

If DFS is now at vertex x and explore edge x → y and encounter status[y] = explored, we can declare x → y is a back edge (a cycle is found as we were previously at vertex y (hence status[y] = explored), go deep to neighbor of y and so on, but we are now at vertex x that is reachable from y but vertex x leads back to vertex y).

The edges in the graph that are not tree edge(s) nor back edge(s) are colored grey. They are called forward or cross edge(s) and currently have limited use (not elaborated).

Now try DFS(0) on the example graph above with this new understanding, especially about the 3 possible status of a vertex (unvisited/normal black circle, explored/blue circle, visited/orange circle) and back edge. Edge 2 → 1 will be discovered as a back edge as it is part of cycle 1 → 3 → 2 → 1 (similarly with Edge 6 → 4 as part of cycle 4 → 5 → 7 → 6 → 4).

We can use following simple recursive function to print out the path stored in array p. Possible follow-up discussion: Can you write this in iterative form? (trivial)

method backtrack(u)
  if (u == -1) stop
  backtrack(p[u]);
  output vertex u

To print out the path from a source vertex s to a target vertex t in a graph, you can call O(V+E) DFS(s) (or BFS(s)) and then O(V) backtrack(t). Example: s = 0 and t = 4, you can call DFS(0) and then backtrack(4). When we call backtrack(4) after executing DFS(0) on the sample graph, we go back from 4 → p[4] = 3 → p[3] = 2 → p[2] = 1 → p[1] = 0 → p[0] = -1 (so 0 is the source) and print the path in reversed order (due to recursion) i.e.: 0 → 1 → 2 → 3 → 4.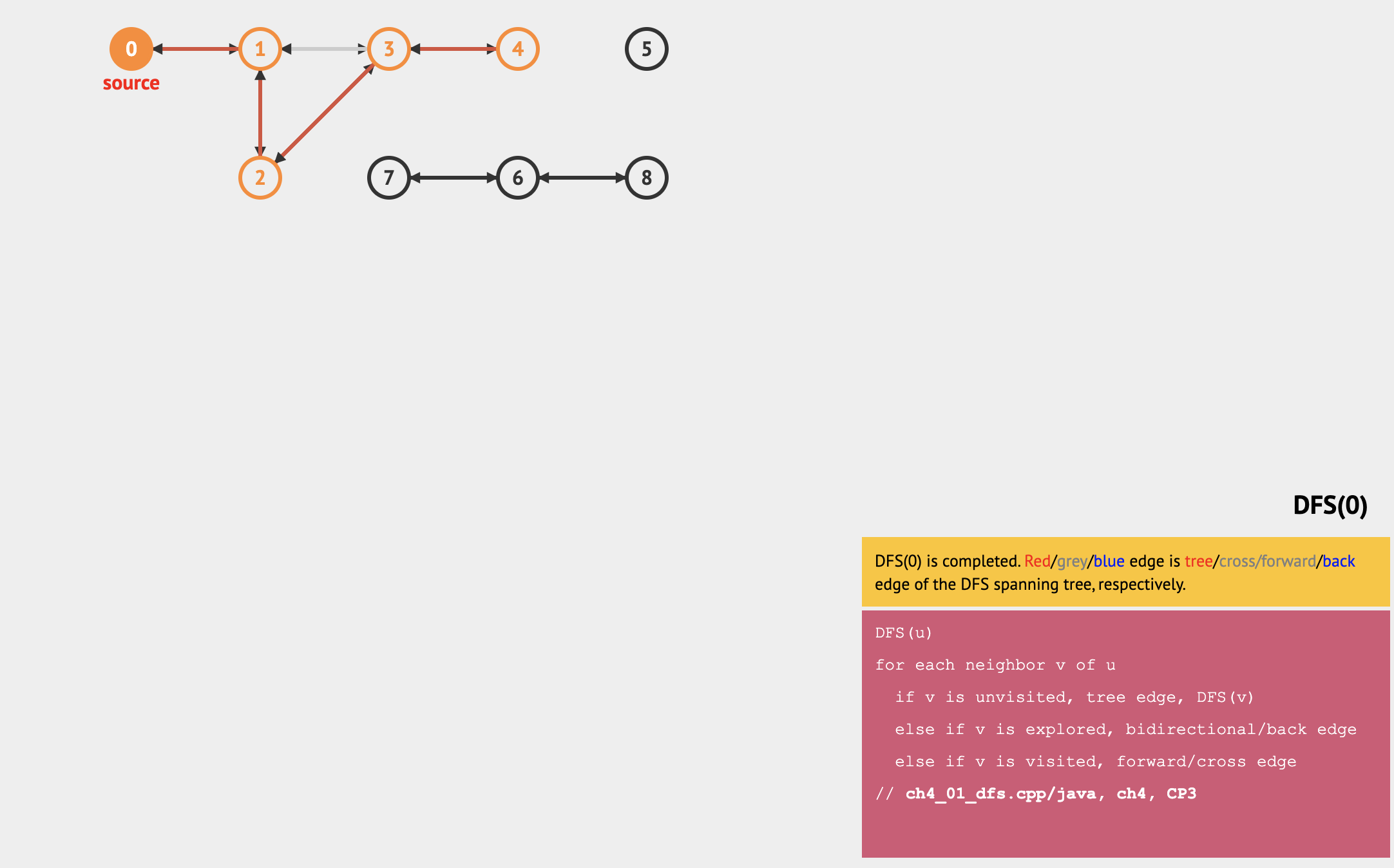

Q4 in midterm practice

Design an algorithm to take an undirected, connected graph G(V,E) and give each of its edge a direction such the following two conditions are satisfied:

1. The resulting directed graph contains a tree all of whose edges point away from the root
2. Any edge that does not belong to the above tree forms a directed cycle with edges of the tree (A directed cycle is a cycle in which all the edges are going the same way)

Answer

We shall run DFS to produce a tree and then flip the edges not in the tree appropriately

• Run DFS. As we traverse the edges during DFS we create the directed edge from parent to child, ensuring that all edges face away from the root. At the same time, we timestamp each node such that we know the order in which we visited them (which will be necessary to easily decide the direction of non-tree edges) This satisfies the first condition.
• We then deal with the remaining edges. Every edge will connect two nodes, and every node is timestamped. We direct non-tree edges from the more recent node to the older node. This ensures that it points back to a node that will form a cycle (and this relies on the traversal ordering provided by DFS)