图论基础

图的逻辑结构和具体实现

一幅图是由节点和边构成的，逻辑结构如下：

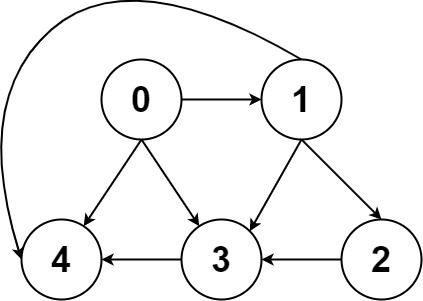
什么叫「逻辑结构」？就是说为了方便研究，我们把图抽象成这个样子。

根据这个逻辑结构，我们可以认为每个节点的实现如下：

/* 图节点的逻辑结构 */
class Vertex {
    int id;
    Vertex[] neighbors;
}

看到这个实现，你有没有很熟悉？它和我们之前说的多叉树节点几乎完全一样：

/* 基本的 N 叉树节点 */
class TreeNode {
    int val;
    TreeNode[] children;
}

所以说，图真的没啥高深的，就是高级点的多叉树而已。

不过呢，上面的这种实现是「逻辑上的」，实际上我们很少用这个 Vertex 类实现图，而是用常说的邻接表和邻接矩阵来实现。

邻接表和邻接矩阵

用邻接表和邻接矩阵的存储方式如下：

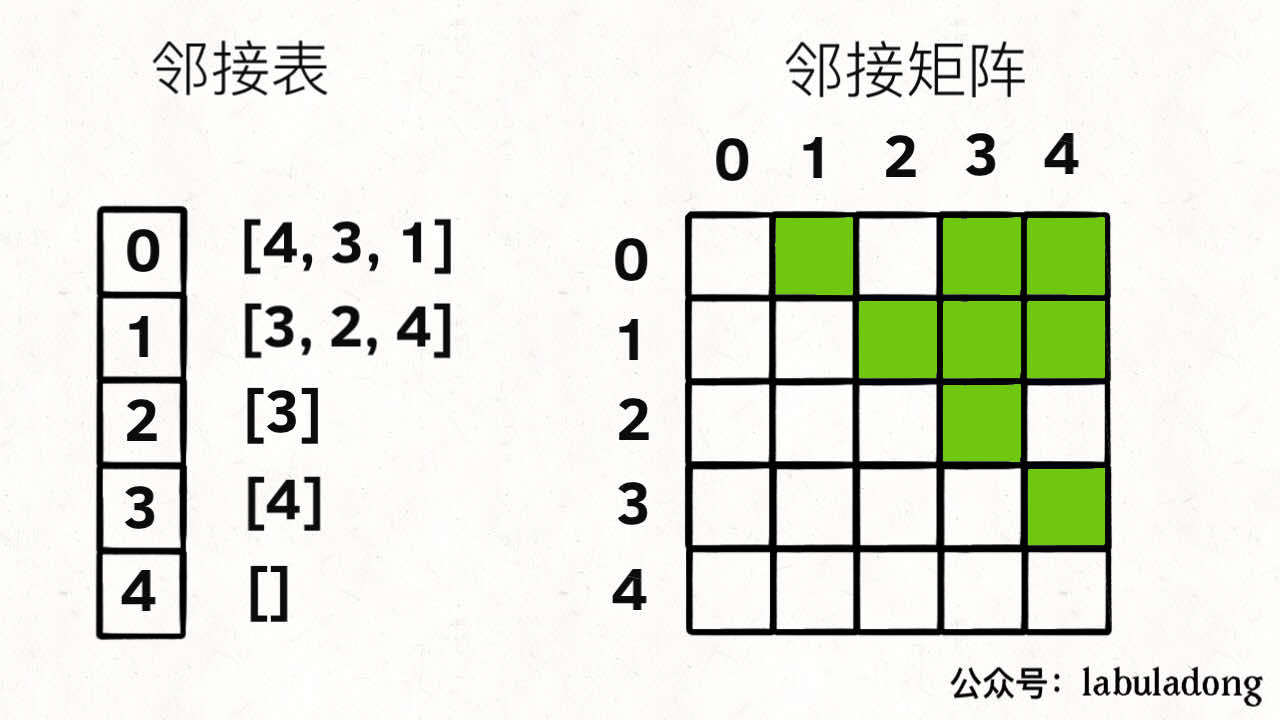
邻接表很直观，我把每个节点 x 的邻居都存到一个列表里，然后把 x 和这个列表关联起来，这样就可以通过一个节点 x 找到它的所有相邻节点。

1. 邻接表，好处是占用的空间少
2. 邻接表无法快速判断两个节点是否相邻(想判断节点 1 是否和节点 3 相邻，我要去邻接表里 1 对应的邻居列表里查找 3 是否存在。)

邻接矩阵则是一个二维布尔数组，我们权且成为 matrix，如果节点 x 和 y 是相连的，那么就把 matrix[x][y] 设为 true（上图中绿色的方格代表 true）。如果想找节点 x 的邻居，去扫一圈 matrix[x][..] 就行了。

1. 需要更多的存储空间。
2. 只要看看 matrix[1][3] 就知道了，效率高。

图的遍历

/* 多叉树遍历框架 */
void traverse(TreeNode root) {
    if (root == null) return;

    for (TreeNode child : root.children)
        traverse(child);
}

图和多叉树最大的区别是，图是可能包含环的，你从图的某一个节点开始遍历，有可能走了一圈又回到这个节点。

所以，如果图包含环，遍历框架就要一个 visited 数组进行辅助：