动态规划

动态规划框架思想

首先，动态规划问题的一般形式就是求最值。

比如说让你求最长递增子序列呀，最小编辑距离呀等等。

核心问题是:求解动态规划的核心问题是穷举。

动态规划三大要素

1. 存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

2. 动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。

3. 只有列出正确的「状态转移方程」，才能正确地穷举。

框架明确

明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。

1. 明确base case
2. 明确状态，进行状态转移
3. 明确选择的方式
4. 定义dp数组/函数的含义

按上面的套路走，最后的结果就可以套这个框架：

# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

第一步要明确两点，「状态」和「选择」。

先说状态，如何才能描述一个问题局面？只要给几个物品和一个背包的容量限制，就形成了一个背包问题呀。所以状态有两个，就是「背包的容量」和「可选择的物品」。

再说选择，也很容易想到啊，对于每件物品，你能选择什么？选择就是「装进背包」或者「不装进背包」嘛。

明白了状态和选择，动态规划问题基本上就解决了，只要往这个框架套就完事儿了：

第二步要明确 dp 数组的定义。

首先看看刚才找到的「状态」，有两个，也就是说我们需要一个二维 dp 数组。

dp[i][w] 的定义如下：对于前 i 个物品，当前背包的容量为 w，这种情况下可以装的最大价值是 dp[i][w]。

算法实战

斐波那契数列

暴力递归

int fib(int N) {
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);
}

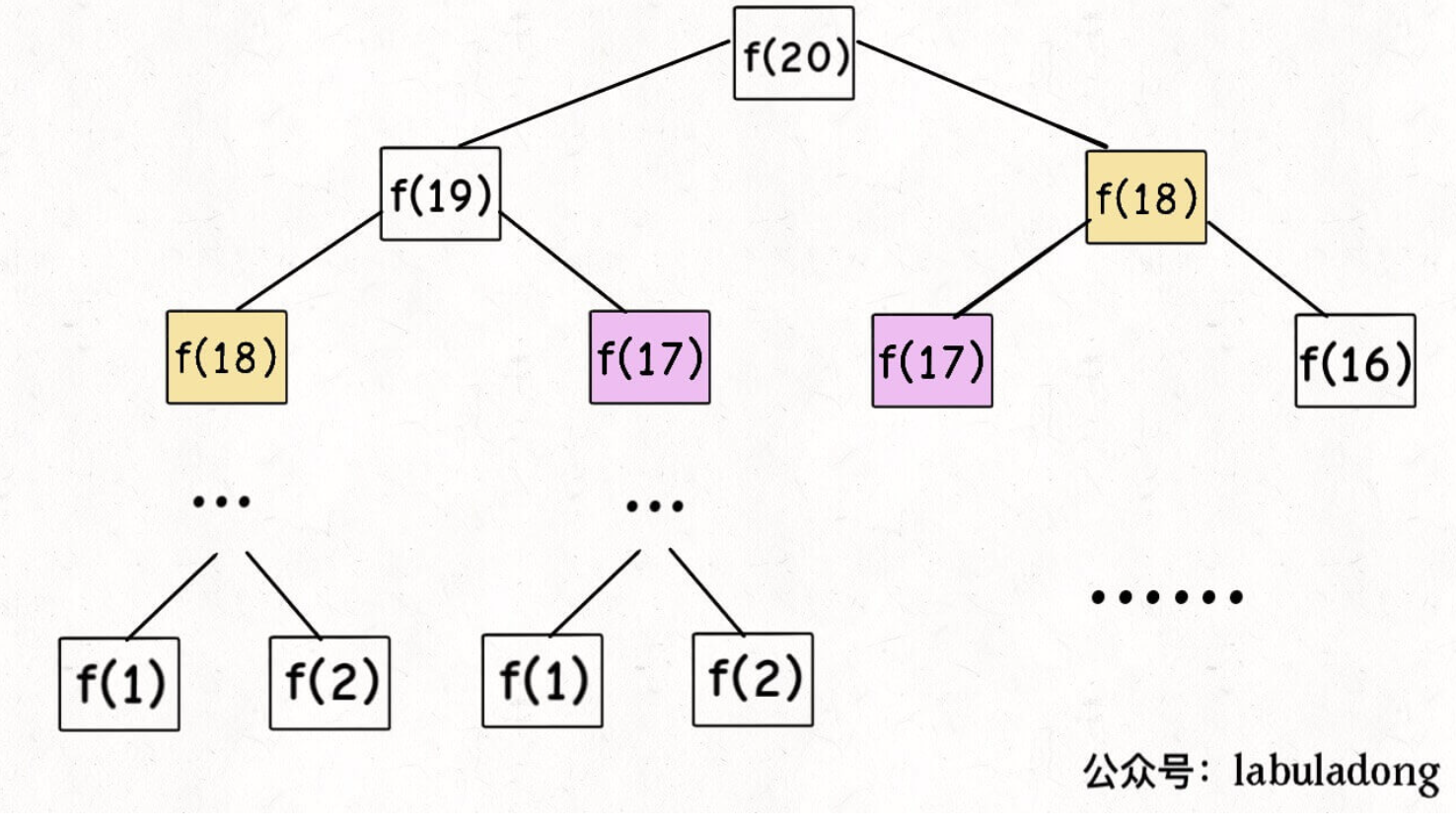
PS：但凡遇到需要递归的问题，最好都画出递归树，这对你分析算法的复杂度，寻找算法低效的原因都有巨大帮助。

递归算法的时间复杂度怎么计算？就是用子问题个数乘以解决一个子问题需要的时间。

首先计算子问题个数，即递归树中节点的总数。显然二叉树节点总数为指数级别，所以子问题个数为 O(2^n)。

然后计算解决一个子问题的时间，在本算法中，没有循环，只有 f(n - 1) + f(n - 2) 一个加法操作，时间为 O(1)。

所以，这个算法的时间复杂度为二者相乘，即 O(2^n)，指数级别，爆炸。

递归函数调用的次数*递归函数本身的复杂度

带备忘录的递归

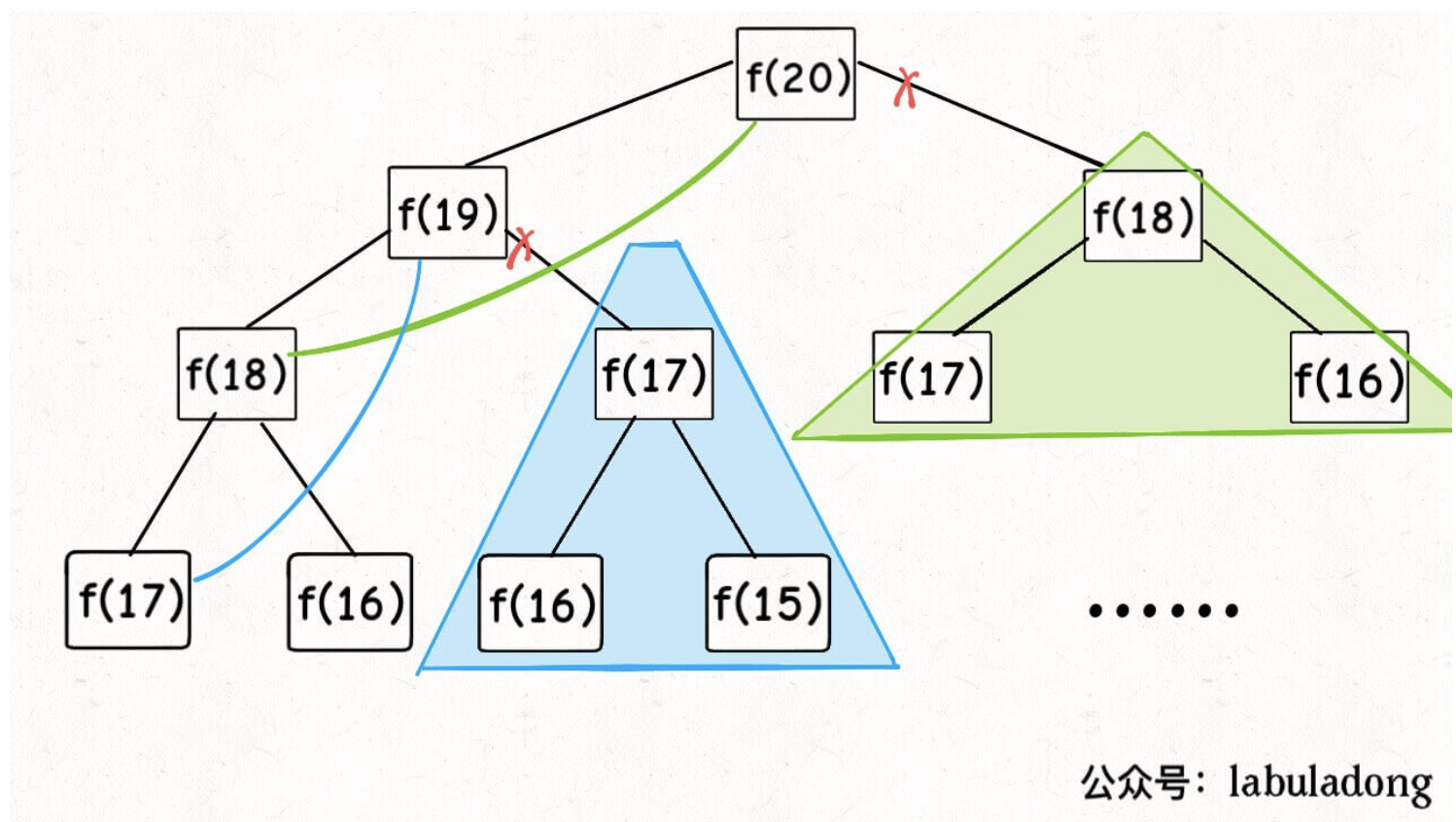
一般使用一个数组充当这个「备忘录」，当然你也可以使用哈希表（字典），思想都是一样的。

俗称剪枝

public int fib_memo(int n) {
    int[] memo = new int[n + 1];
    return helper(memo, n);
}

public int helper(int[] memo, int n) {
  // 备忘录全部初始化为0
    if (memo[n] != 0) return memo[n];

    // base case
    if (n == 0 || n == 1) return n;

    memo[n] = helper(memo, n - 1) + helper(memo, n - 2);

    return memo[n];
}

注意备忘录是申请一个N+1 长度的数组

因为我们要操作memo的索引是从0开始的，所以为了保证最后边界的合法性，一定是从N+1开始的

Python 解法

def fib(self, n: int) -> int:
    memo = (n + 1) * [0]

    def helper(memo: List[int], n: int) -> int:
        # memo
        if memo[n] != 0:
            return memo[n]

        # base case
        if n == 1 or n == 0:
            return n

        memo[n] = helper(memo, n - 1) + helper(memo, n - 2)

        return memo[n]

    return helper(memo, n)

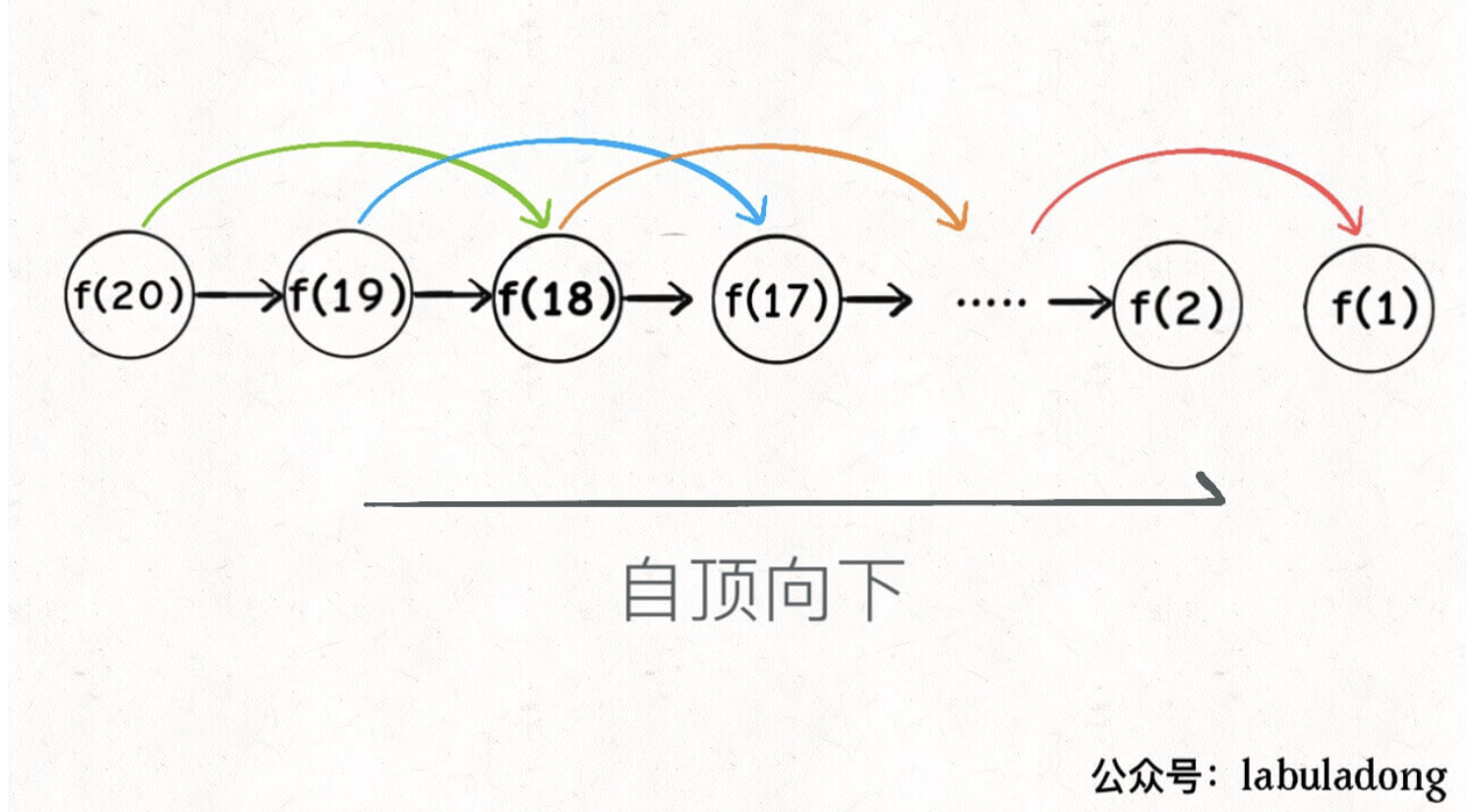
dp 数组的迭代解法

public int fib_bottom_to_up(int n) {
    if (n == 0) return 0;

    int[] dp = new int[n + 1];

    dp[0] = 0;
    dp[1] = 1;

    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    return dp[n];
}

def fib2(self, n: int) -> int:
    if n == 0: return 0
    dp = (n + 1) * [0]

    dp[0] = 0
    dp[1] = 1

    for i in range(2, n + 1):
        dp[i] = dp[i - 1] + dp[i - 2]

    return dp[n]

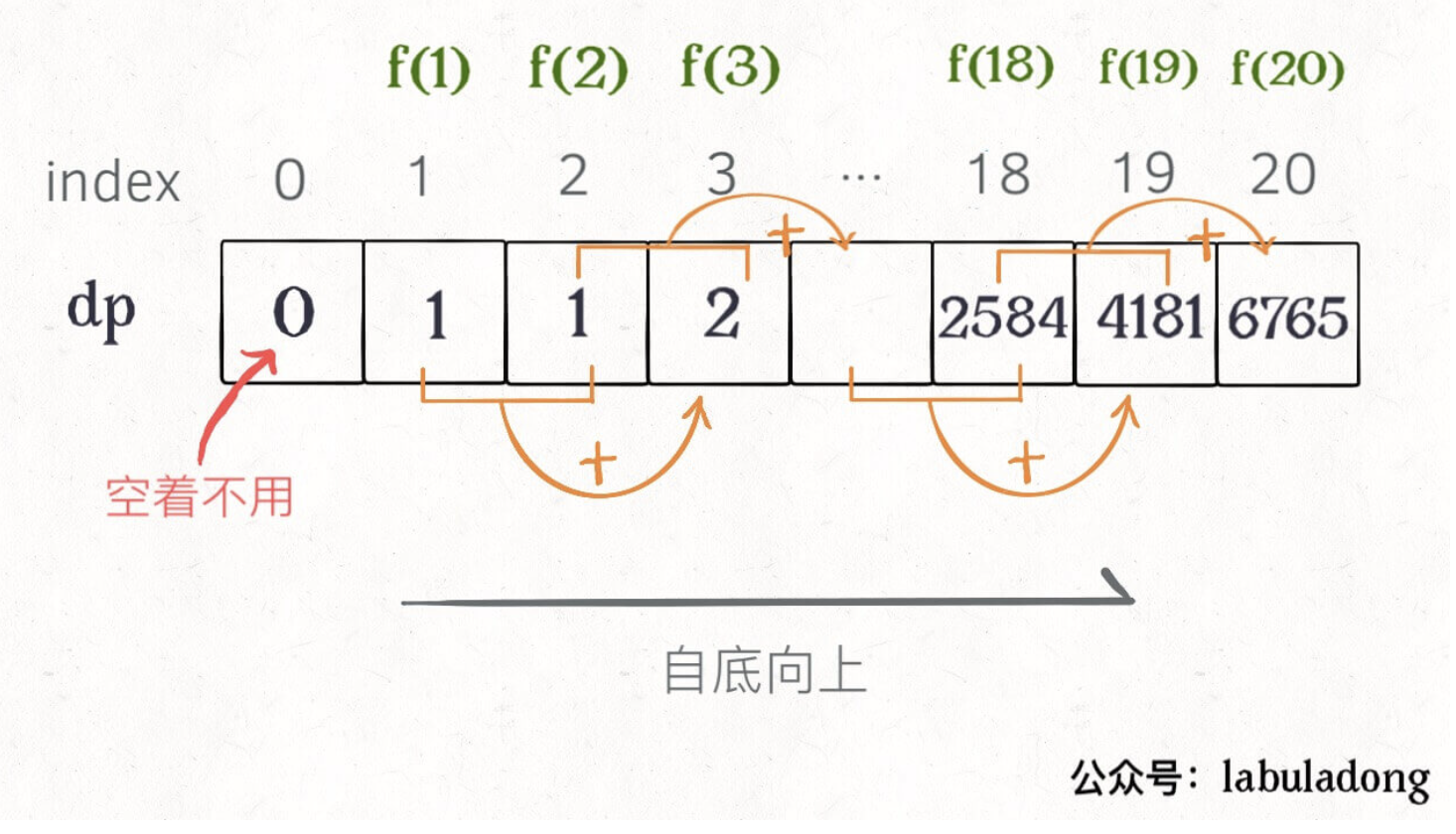
进一步优化(状态压缩)

状态转移方程

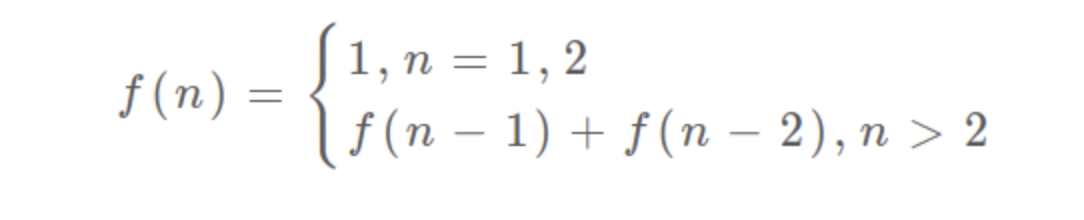
public int fib_dp(int n) {
    if (n <= 2) return 1;

    int sum = 0;
    int n1 = 0;
    int n2 = 1;

    for (int i = 2; i <= n; i++) {
        sum = n1 + n2;
        n1 = n2;
        n2 = sum;
    }
    return sum;
}

int fib(int n) {
    if (n < 1) return 0;
    if (n == 2 || n == 1) 
        return 1;
    int prev = 1, curr = 1;
    for (int i = 3; i <= n; i++) {
        int sum = prev + curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

这个技巧就是所谓的「状态压缩」，如果我们发现每次状态转移只需要 DP table 中的一部分，那么可以尝试用状态压缩来缩小 DP table 的大小，只记录必要的数据，上述例子就相当于把DP table 的大小从 n 缩小到 2。后续的动态规划章节中我们还会看到这样的例子，一般来说是把一个二维的 DP table 压缩成一维，即把空间复杂度从 O(n^2) 压缩到 O(n)。

凑零钱问题

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

示例 2：

输入：coins = [2], amount = 3
输出：-1

示例 3：

输入：coins = [1], amount = 0
输出：0

示例 4：

输入：coins = [1], amount = 1
输出：1

示例 5：

输入：coins = [1], amount = 2
输出：2

暴力递归(带备忘录的)

首先，这个问题是动态规划问题，因为它具有「最优子结构」的。要符合「最优子结构」，子问题间必须互相独立。啥叫相互独立？你肯定不想看数学证明，我用一个直观的例子来讲解。

为什么说它符合最优子结构呢？比如你想求 amount = 11 时的最少硬币数（原问题），如果你知道凑出 amount = 10 的最少硬币数（子问题），你只需要把子问题的答案加一（再选一枚面值为 1 的硬币）就是原问题的答案。因为硬币的数量是没有限制的，所以子问题之间没有相互制，是互相独立的。

那么，既然知道了这是个动态规划问题，就要思考如何列出正确的状态转移方程？

1、确定 base case，这个很简单，显然目标金额 amount 为 0 时算法返回 0，因为不需要任何硬币就已经凑出目标金额了。

2、确定「状态」，也就是原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的「状态」就是目标金额 amount。

3、确定「选择」，也就是导致「状态」产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值，就是你的「选择」。

4、明确 dp 函数/数组的定义。我们这里讲的是自顶向下的解法，所以会有一个递归的 dp 函数，一般来说函数的参数就是状态转移中会变化的量，也就是上面说到的「状态」；函数的返回值就是题目要求我们计算的量。就本题来说，状态只有一个，即「目标金额」，题目要求我们计算凑出目标金额所需的最少硬币数量。所以我们可以这样定义 dp 函数：

dp(n) 的定义：输入一个目标金额 n，返回凑出目标金额 n 的最少硬币数量。

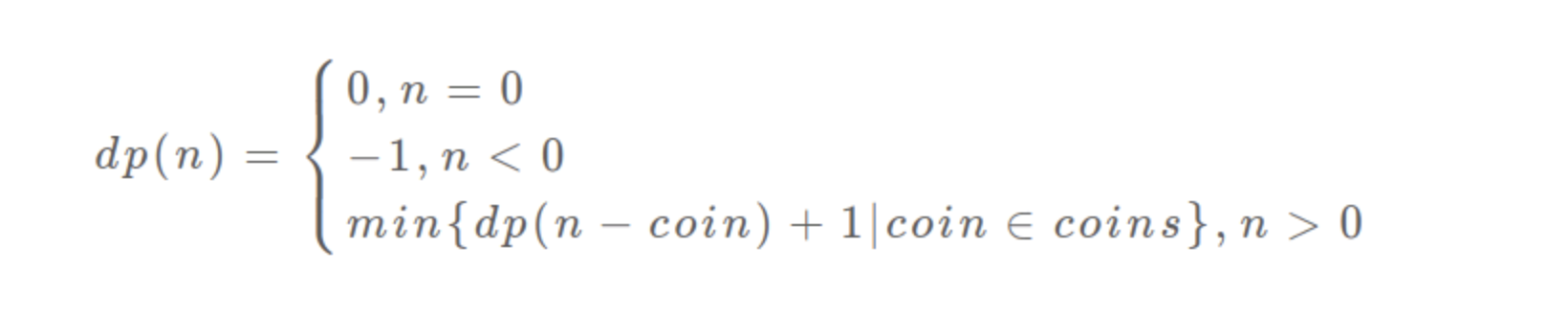
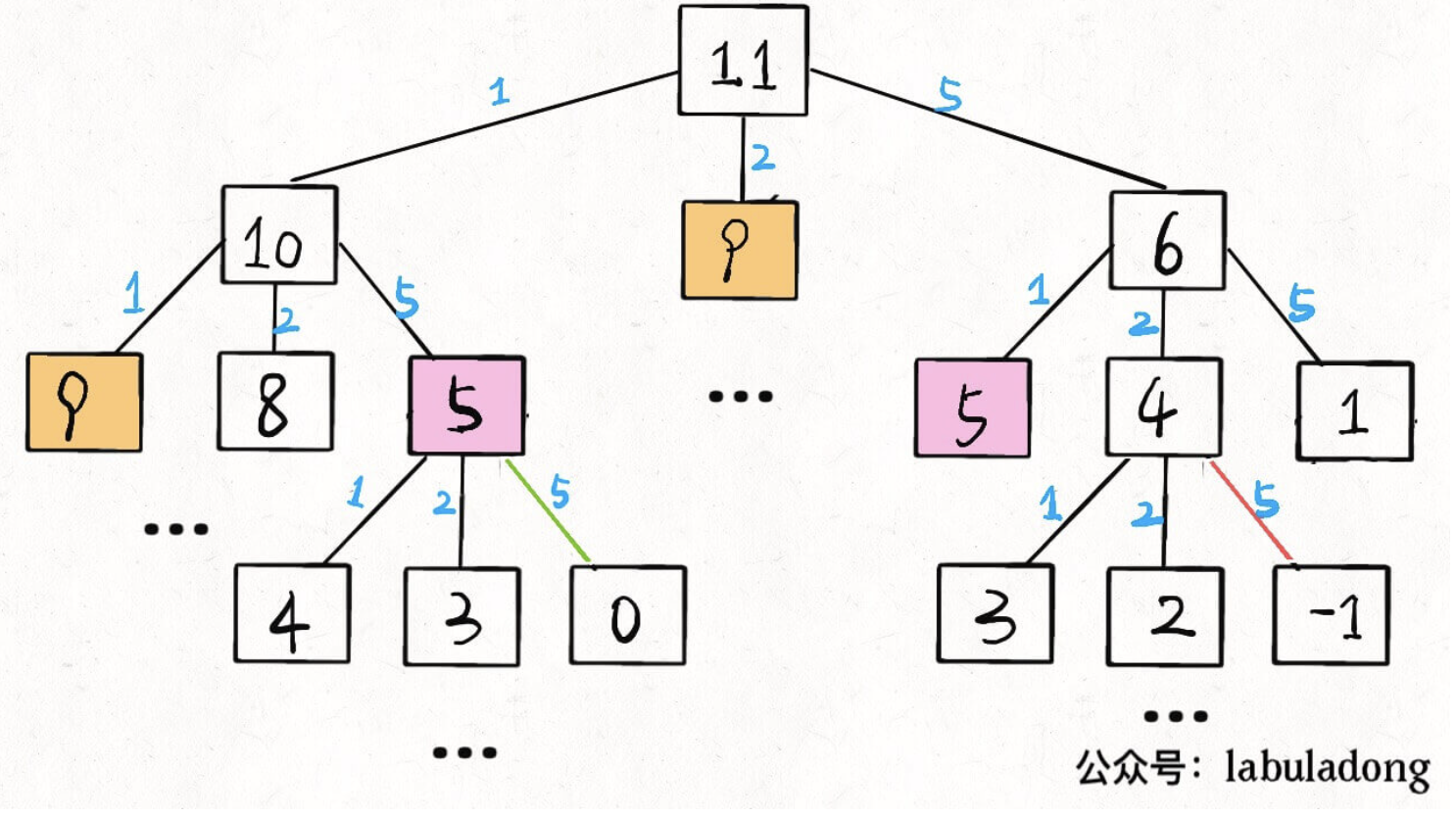
递归算法的时间复杂度分析：子问题总数 x 每个子问题的时间。

子问题总数为递归树节点个数，这个比较难看出来，是 O(n^k)，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为 O(k)。所以总时间复杂度为 O(k * n^k)，指数级别。

Java

int [] memo;
public int coinChange(int[] coins, int amount) {
    memo = new int[amount+1];
    Arrays.fill(memo,-666);
    return helper(coins, amount);
}

public int helper(int[] coins, int amount){
    if (amount==0) return 0;
    if (amount<0) return -1;
    if (memo[amount]!=-666) return memo[amount];

    int res = Integer.MAX_VALUE;
    for (int coin: coins){
        int subProblem = helper(coins,amount-coin);
        if(subProblem==-1) continue;
        res = Math.min(res,subProblem+1);
    }

    memo[amount] = res==Integer.MAX_VALUE?-1:res;
    return  memo[amount];
    
}

Python

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        memo = (amount + 1) * [-666]

        def helper(coins: List[int], amount: int) -> int:
            # base case
            if amount == 0: return 0
            if amount < 0: return -1
            # memo iteration
            if memo[amount] != -666: return memo[amount]

            res = sys.maxsize
            for coin in coins:
                subProblems = helper(coins, amount - coin)
                if subProblems < 0: continue
                res = min(res, subProblems + 1)
            
            memo[amount] = -1 if res == sys.maxsize else res

            return memo[amount]

        return helper(coins, amount)

def coinChange(coins: List[int], amount: int):
    # 备忘录
    memo = dict()
    def dp(n):
        # 查备忘录，避免重复计算
        if n in memo: return memo[n]
        # base case
        if n == 0: return 0
        if n < 0: return -1
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            if subproblem == -1: continue
            res = min(res, 1 + subproblem)

        # 记入备忘录
        memo[n] = res if res != float('INF') else -1
        return memo[n]

    return dp(amount)

dp 数组的迭代解法

当然，我们也可以自底向上使用 dp table 来消除重叠子问题，关于「状态」「选择」和 base case 与之前没有区别，dp 数组的定义和刚才 dp 函数类似，也是把「状态」，也就是目标金额作为变量。不过 dp 函数体现在函数参数，而 dp 数组体现在数组索引：

dp 数组的定义：当目标金额为 i 时，至少需要 dp[i] 枚硬币凑出。

根据我们文章开头给出的动态规划代码框架可以写出如下解法：

int coinChange(vector<int>& coins, int amount) {
    // 数组大小为 amount + 1，初始值也为 amount + 1
    vector<int> dp(amount + 1, amount + 1);
    // base case
    dp[0] = 0;
    // 外层 for 循环在遍历所有状态的所有取值
    for (int i = 0; i < dp.size(); i++) {
        // 内层 for 循环在求所有选择的最小值
        for (int coin : coins) {
            // 子问题无解，跳过
            if (i - coin < 0) continue;
            dp[i] = min(dp[i], 1 + dp[i - coin]);
        }
    }
    return (dp[amount] == amount + 1) ? -1 : dp[amount];
}

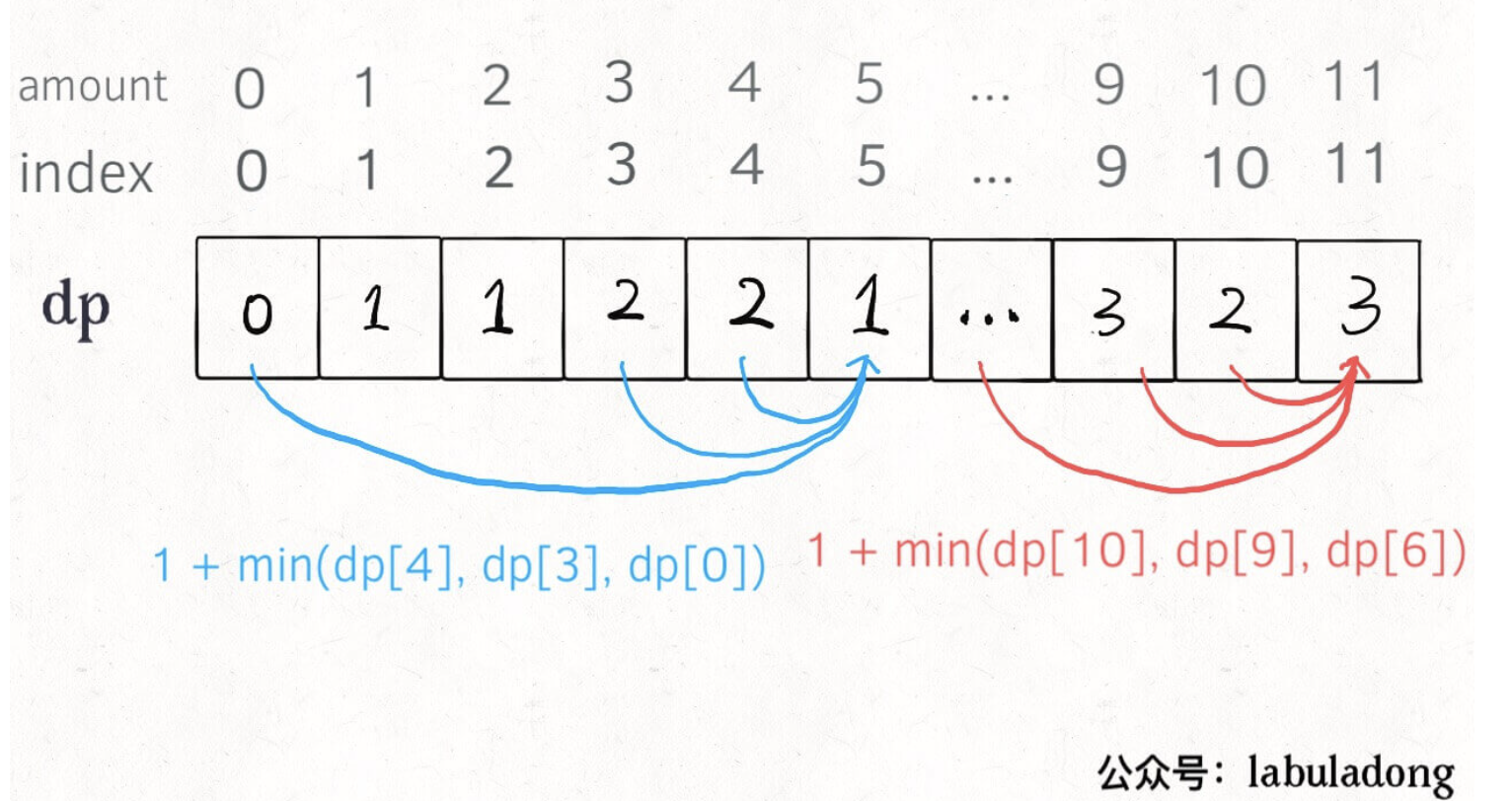
PS：为啥 dp 数组初始化为 amount + 1 呢，因为凑成 amount 金额的硬币数最多只可能等于 amount（全用 1 元面值的硬币），所以初始化为 amount + 1 就相当于初始化为正无穷，便于后续取最小值。

72. 编辑距离

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

思路

https://mp.weixin.qq.com/s?__biz=MzAxODQxMDM0Mw==&mid=2247484484&idx=1&sn=74594297022c84952162a68b7f739133&chksm=9bd7fa4caca0735a1364dd13901311ecd6ec4913c8db05a1ff6cae8f069627eebe8d651bbeb1&scene=21#wechat_redirect

解决两个字符串的动态规划问题，一般都是用两个指针i,j分别指向两个字符串的最后，然后一步步往前走，缩小问题的规模。

递归解法：

先梳理一下之前的思路：

base case 是i走完s1或j走完s2，可以直接返回另一个字符串剩下的长度。

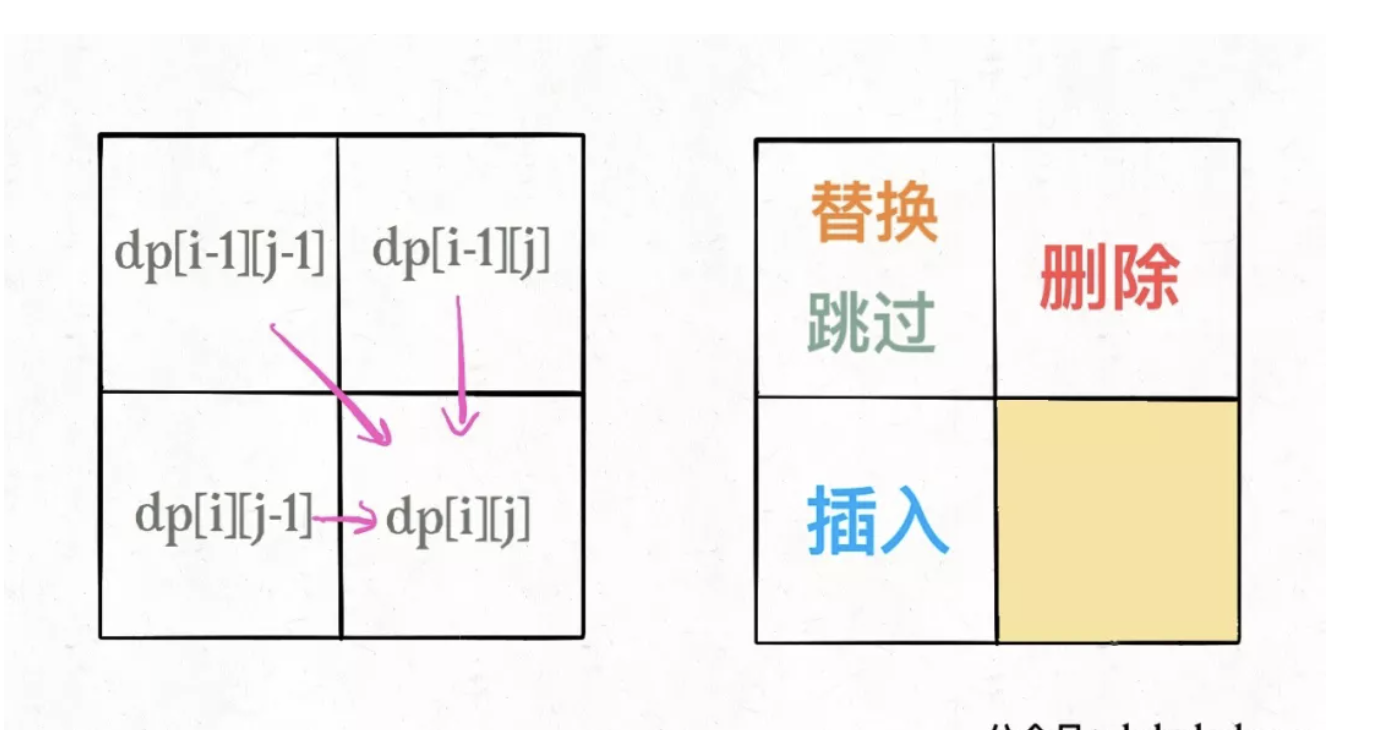
对于每对儿字符s1[i]和s2[j]，可以有四种操作：

if s1[i] == s2[j]:
    啥都别做（skip）
    i, j 同时向前移动
else:
    三选一：
        插入（insert）
        删除（delete）
        替换（replace）

有这个框架，问题就已经解决了。读者也许会问，这个「三选一」到底该怎么选择呢？很简单，全试一遍，哪个操作最后得到的编辑距离最小，就选谁。这里需要递归技巧，理解需要点技巧，先看下代码：

class Solution:
    def minDistance(self, s1: str, s2: str) -> int:
        memo = dict()

        def dp(i, j):
            # base case
            if i == -1:
                return j + 1
            if j == -1:
                return i + 1

            if (i, j) in memo:
                return memo[(i, j)]

            if s1[i] == s2[j]:
                memo[(i, j)] = dp(i - 1, j - 1)
            else:
                memo[(i, j)] = min(
                    dp(i, j - 1) + 1,
                    dp(i - 1, j) + 1,
                    dp(i - 1, j - 1) + 1
                )
            return memo[(i, j)]

        return dp(len(s1) - 1, len(s2) - 1)


if __name__ == '__main__':
    sol = Solution
    sol.minDistance(sol, "horse", "ros")

一些细节问题

if s1[i] == s2[j]:
    return dp(i - 1, j - 1)  # 啥都不做
# 解释：
# 本来就相等，不需要任何操作
# s1[0..i] 和 s2[0..j] 的最小编辑距离等于
# s1[0..i-1] 和 s2[0..j-1] 的最小编辑距离
# 也就是说 dp(i, j) 等于 dp(i-1, j-1)

dp(i, j - 1) + 1,    # 插入
# 解释：
# 我直接在 s1[i] 插入一个和 s2[j] 一样的字符
# 那么 s2[j] 就被匹配了，前移 j，继续跟 i 对比
# 别忘了操作数加一

dp(i - 1, j) + 1,    # 删除
# 解释：
# 我直接把 s[i] 这个字符删掉
# 前移 i，继续跟 j 对比
# 操作数加一

dp(i - 1, j - 1) + 1 # 替换
# 解释：
# 我直接把 s1[i] 替换成 s2[j]，这样它俩就匹配了
# 同时前移 i，j 继续对比
# 操作数加一

Dp Table 方法

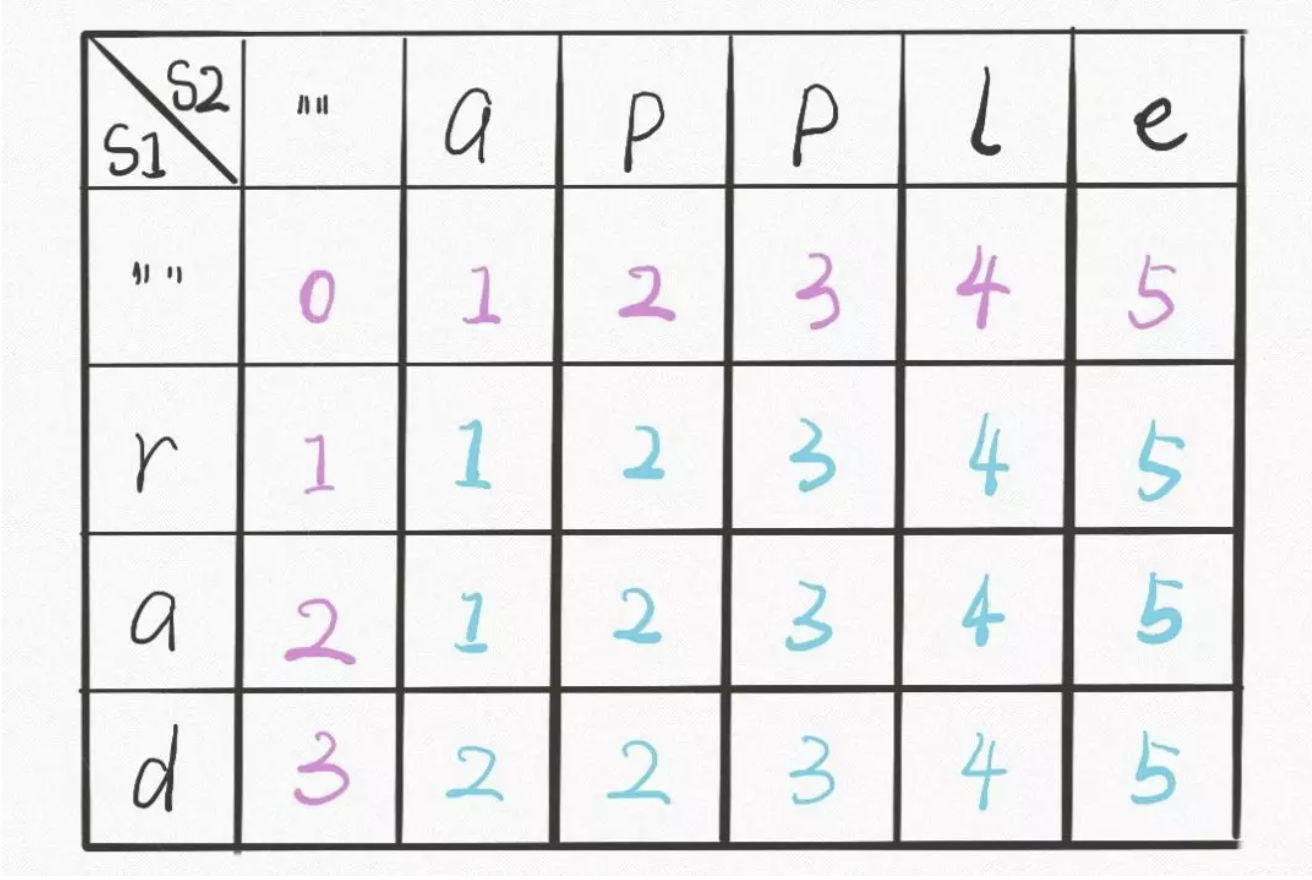
有了之前递归解法的铺垫，应该很容易理解。dp 函数的 base case 是i,j等于 -1，而数组索引至少是 0，所以 dp 数组会偏移一位，dp[..][0]和dp[0][..]对应 base case。。

既然 dp 数组和递归 dp 函数含义一样，也就可以直接套用之前的思路写代码，唯一不同的是，DP table 是自底向上求解，递归解法是自顶向下求解：

package dp;

public class MinDistance {
    public int minDistance(String s1, String s2) {
        int m = s1.length();
        int n = s2.length();
        // dp[i][j] 用来存储s1[0...i-1] 变成s2[0..j-1]的最小距离
        // 因为索引不能为-1，为非法，所以为0
        int dp[][] = new int[m + 1][n + 1];
        // base case
        for (int i = 1; i <= m; i++) {
            dp[i][0] = i;
        }
        for (int j = 1; j <= n; j++) {
            dp[0][j] = j;
        }

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    dp[i][j] = min(
                            dp[i - 1][j - 1] + 1,
                            dp[i - 1][j] + 1,
                            dp[i][j - 1] + 1
                    );

                }

            }

        }

        return dp[m][n];
    }


    public int min(int a, int b, int c) {
        return Math.min(a, Math.min(b, c));
    }
}

0,1 背包问题

package dp;

public class Knapsack {
    /**
     * @param w   背包的容量
     * @param n   物品的个数
     * @param wt  物品i的重量是wt[i]
     * @param val 物品的价值是val[i]
     * @return
     */
    public int knapsack(int w, int n, int[] wt, int[] val) {
        // dp[i][w] 在前 i 个物品的时候，当背包的容量为w的时候，
        // 可以装的最大价值是
        int[][] dp = new int[n + 1][w + 1];

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= w; j++) {
                if (j - wt[i-1] < 0) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(
                            dp[i - 1][j - wt[i - 1]] + val[i - 1],
                            dp[i - 1][j]
                    );
                }

            }

        }
        return dp[n][w];
    }

    public int knapsack2(int W, int N, int[] wt, int[] val) {
        int[][] dp = new int[N + 1][W + 1];

        for (int i = 1; i <= N; i++) {
            for (int w = 1; w <= W; w++) {
                if (w - wt[i-1] < 0) {
                    dp[i][w] = dp[i - 1][w];
                } else {
                    dp[i][w] = Math.max(
                            dp[i - 1][w],
                            dp[i - 1][w - wt[i-1]] + val[i - 1]
                    );
                }
            }
        }

        return dp[N][W] ;
    }


        public static void main(String[] args) {
        Knapsack knapsack = new Knapsack();
        int[] wt = {2, 1, 3};
        int[] val = {4, 2, 3};
        System.out.println(knapsack.knapsack2(4, 3, wt, val));
        System.out.println(knapsack.knapsack(4, 3, wt, val));
    }
}

518. 零钱兑换 II

难度中等572

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。

题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10] 
输出：1

解题思路

第一步要明确两点，「状态」和「选择」。

状态有两个，就是「背包的容量」和「可选择的物品」，选择就是「装进背包」或者「不装进背包」嘛，背包问题的套路都是这样。

明白了状态和选择，动态规划问题基本上就解决了，只要往这个框架套就完事儿了：

for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 计算(选择1，选择2...)

第二步要明确 dp 数组的定义。

首先看看刚才找到的「状态」，有两个，也就是说我们需要一个二维 dp 数组。

dp[i][j] 的定义如下：

若只使用前 i 个物品（可以重复使用），当背包容量为 j 时，有 dp[i][j] 种方法可以装满背包。

换句话说，翻译回我们题目的意思就是：

若只使用 coins 中的前 i 个硬币的面值，若想凑出金额 j**，有** dp[i][j] 种凑法。

经过以上的定义，可以得到：

base case 为 dp[0][..] = 0， dp[..][0] = 1。因为如果不使用任何硬币面值，就无法凑出任何金额；如果凑出的目标金额为 0，那么“无为而治”就是唯一的一种凑法。

我们最终想得到的答案就是 dp[N][amount]，其中 N 为 coins 数组的大小。

大致的伪码思路如下：

int dp[N+1][amount+1]
dp[0][..] = 0
dp[..][0] = 1


for i in [1..N]:
    for j in [1..amount]:
        把物品 i 装进背包,
        不把物品 i 装进背包
return dp[N][amount]

第三步，根据「选择」，思考状态转移的逻辑。

注意，我们这个问题的特殊点在于物品的数量是无限的，所以这里和之前写的 0-1 背包问题 文章有所不同。

如果你不把这第 i 个物品装入背包，也就是说你不使用 coins[i] 这个面值的硬币，那么凑出面额 j 的方法数 dp[i][j] 应该等于 dp[i-1][j]，继承之前的结果。

如果你把这第 i 个物品装入了背包，也就是说你使用 coins[i] 这个面值的硬币，那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]]。

首先由于 i 是从 1 开始的，所以 coins 的索引是 i-1 时表示第 i 个硬币的面值。

dp[i][j-coins[i-1]] 也不难理解，如果你决定使用这个面值的硬币，那么就应该关注如何凑出金额 j - coins[i-1]。

比如说，你想用面值为 2 的硬币凑出金额 5，那么如果你知道了凑出金额 3 的方法，再加上一枚面额为 2 的硬币，不就可以凑出 5 了嘛。

综上就是两种选择，而我们想求的 dp[i][j] 是「共有多少种凑法」，所以 dp[i][j] 的值应该是以上两种选择的结果之和：

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= amount; j++) {
        if (j - coins[i-1] >= 0)
            dp[i][j] = dp[i - 1][j] 
                     + dp[i][j-coins[i-1]];
return dp[N][W]

PS：有的读者在这里可能会有疑问，不是说可以重复使用硬币吗？那么如果我确定「使用第 i 个面值的硬币」，我怎么确定这个面值的硬币被使用了多少枚？简单的一个 dp[i][j-coins[i-1]] 可以包含重复使用第 i 个硬币的情况吗？

对于这个问题，建议你再仔回头细阅读一下我们对 dp 数组的定义，然后把这个定义代入 dp[i][j-coins[i-1]] 看看：

若只使用前 i 个物品（可以重复使用），当背包容量为 j-coins[i-1] 时，有 dp[i][j-coins[i-1]] 种方法可以装满背包。

看到了吗，dp[i][j-coins[i-1]] 也是允许你使用第 i 个硬币的，所以说已经包含了重复使用硬币的情况，你一百个放心。

最后一步，把伪码翻译成代码，处理一些边界情况。

我用 Java 写的代码，把上面的思路完全翻译了一遍，并且处理了一些边界问题：

public int change(int amount, int[] coins) {
    // dp table dp[i][amount]
    // use or not use?
    
    int N = coins.length;
    int[][] dp = new int[N+1][amount+1];

    // base case
    // amount = 0, return 1
    for(int i=0;i<=N;i++){
        dp[i][0] = 1;
    }

    for (int i =1; i<=N;i++){
        for(int j = 1; j<= amount;j++){
            if (j - coins[i-1]>=0){
                dp[i][j] = dp[i-1][j]+dp[i][j-coins[i-1]];
            } else{
                dp[i][j] = dp[i-1][j];
            }
        }
    }

    return dp[N][amount];


}

而且，我们通过观察可以发现，dp 数组的转移只和 dp[i][..] 和 dp[i-1][..] 有关，所以可以压缩状态，进一步降低算法的空间复杂度：

int change(int amount, int[] coins) {
    int n = coins.length;
    int[] dp = new int[amount + 1];
    dp[0] = 1; // base case
    for (int i = 0; i < n; i++)
        for (int j = 1; j <= amount; j++)
            if (j - coins[i] >= 0)
                dp[j] = dp[j] + dp[j-coins[i]];


    return dp[amount];
}

这个解法和之前的思路完全相同，将二维 dp 数组压缩为一维，时间复杂度 O(N*amount)，空间复杂度 O(amount)。

53. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [0]
输出：0

示例 4：

输入：nums = [-1]
输出：-1

示例 5：

输入：nums = [-100000]
输出：-100000

题解1:

public int maxSubArray(int[] nums) {
    /**
     * 输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
     * 输出：6
     * 解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
     */

    // 1. 定义初始化值
    int pre = 0;
    int ans = Integer.MIN_VALUE;
    // 2. 定义递推公式： max{f(i)}= max{num, f(i-1)}

    // 增强for循环的底层原理需要通过iterator来实现接口
    for (int num : nums) {
        pre = Math.max(pre + num, num);
        ans = Math.max(ans, pre);
    }

    return ans;
}

思路使用的是

KADANE'S ALGORITHM

也就是上图的含义

Index	0	1	2	3	4
Value	1	9	-9	-8	-6
Cur_Max	1	10	1	-7	-6
Ans_Max	1	10	10	10	10