二分查找（binary search）
Yuxuan Wu Lv13
2021-07-04 06:58:23 2.6k Words 11 Mins

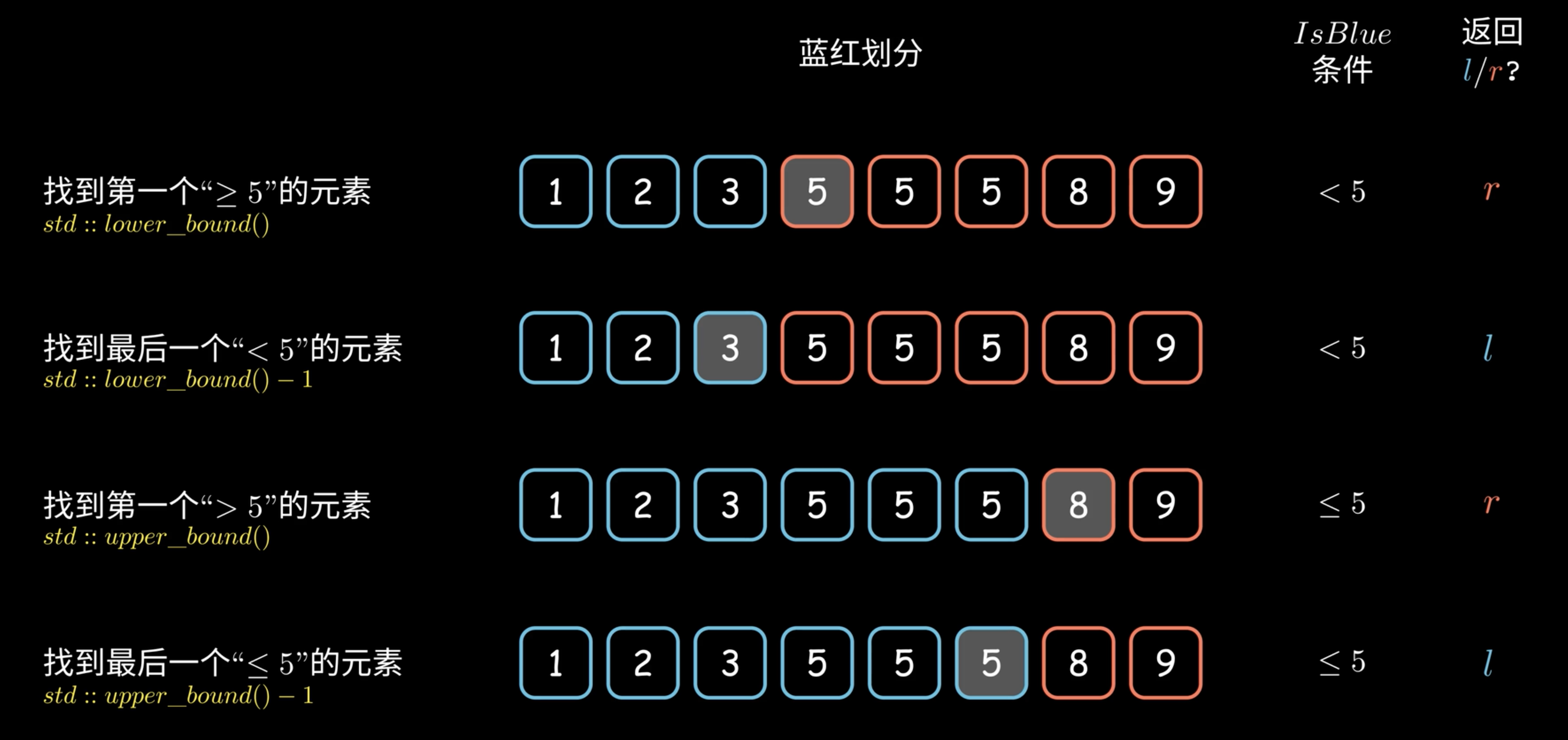
Binary Search两大基本原则

  1. 每次都要缩减搜索区域
  2. 每次缩减不能排除潜在的答案

三大模版

  • 找一个准确值
    • 循环条件是left<=right
    • 缩减搜索空间 left = mid+1， right=mid-1
  • 找一个模糊值（比4大的最小数）
    • 循环条件：left<right
    • 缩减搜索空间：left = mid, right= mid-1
  • 万用型
    • 循环条件 left < right - 1
    • 缩减搜索空间：left = mid, right = mid

704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

  1. 你可以假设 nums 中的所有元素是不重复的。
  2. n 将在 [1, 10000]之间。
  3. nums 的每个元素都将在 [-9999, 9999]之间。

方法1:朴素算法（不是二分查找，低效）

  • 时间复杂度还是O(n)
  • 这里没有用到二分查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length-1;

        while(left<=right){
            if(nums[left]==target) return left;
            if(nums[right]==target) return right;
            left++;
            right--;
        }

        return -1;

    }
}

方法2：二分查找（O(logn)）

伪代码如下：

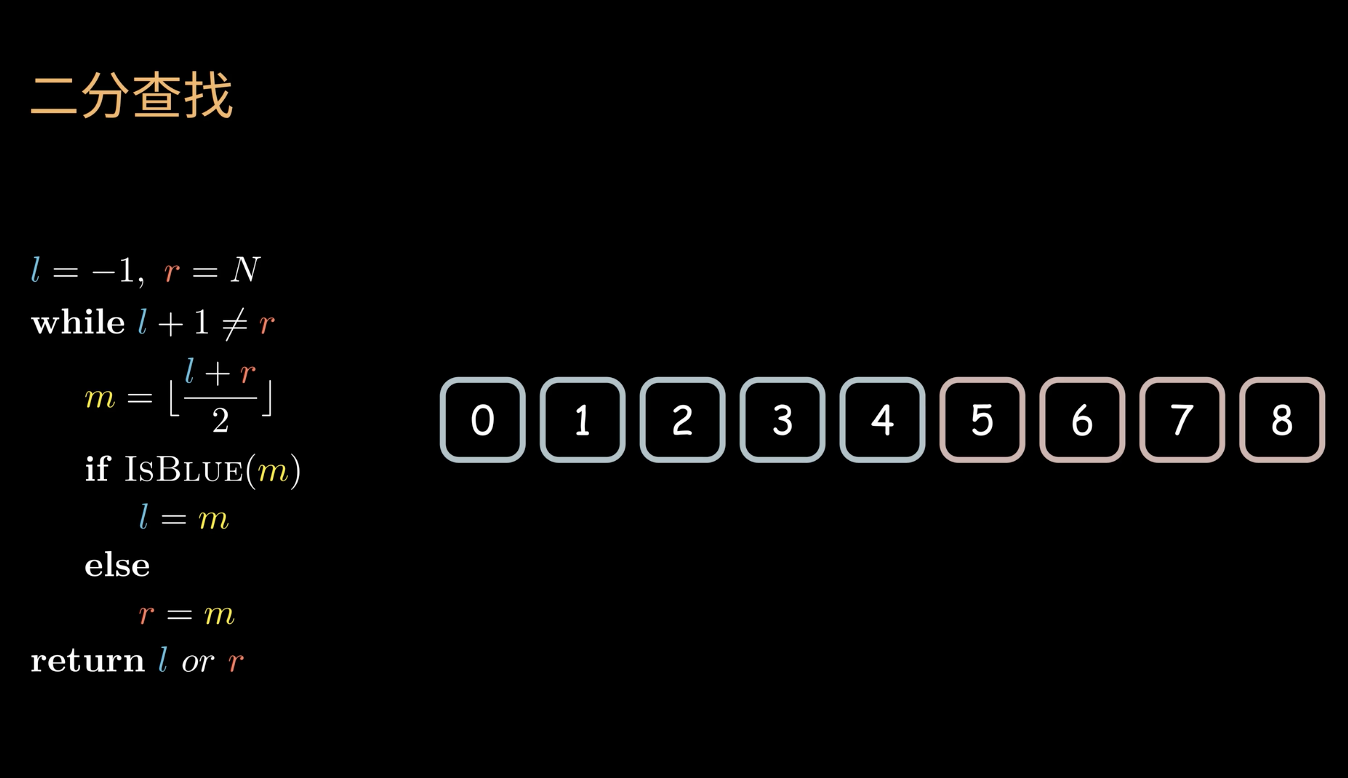
image-20210714091055281

  • 确定双指针的起点位置，注意这个算法的设计较为不一样
  • 左节点为-1，右节点为N
  • 循环的终止条件是l+1!=r
  • 这里的二分查找是将左右两边分为红色和蓝色的区域
  • 注意这里的if条件判断的是蓝色边界的条件
  • 先选择pivot number，m
    • 同时注意int 是向下取整的
  • 循环结束的条件是刚好lr在蓝红边界
  • 然后判断落点是在蓝色区间还是红色区间，
  • 然后将对应的左节点或者右节点变为m
  • 最后需要根据实际情况来判断返回的是l还是r
    • return left or right

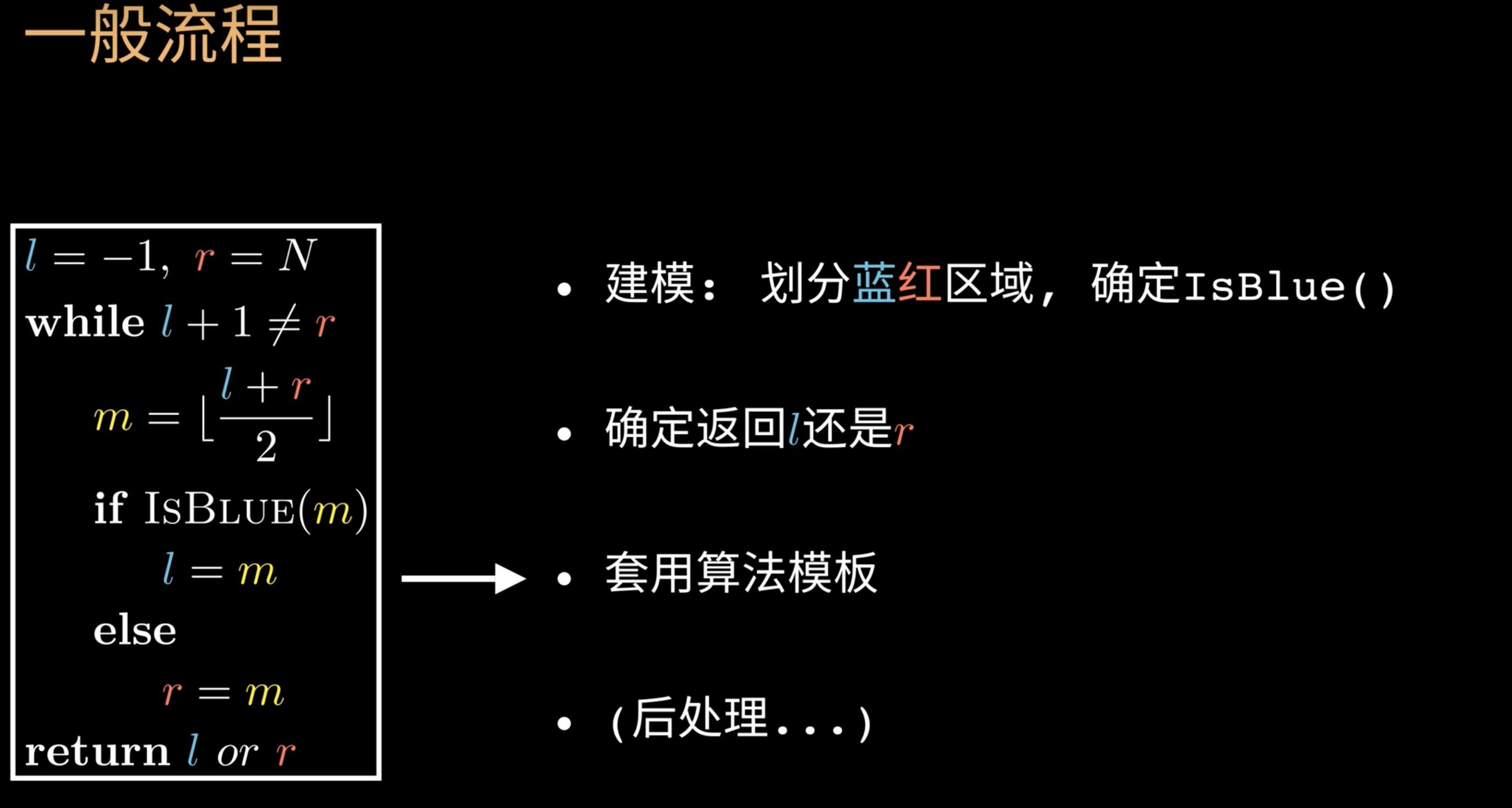
image-20210714101531521

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
package sorting;

public class BinarySearch {
    public static int binarySearch(int[] nums, int target) {
        int left = -1;
        int right = nums.length;
        while (left + 1 != right) {
            int m = (left + right) / 2;
            if (nums[m] < target) {
                left = m;
            } else {
                right = m;
            }
        }
        // 这里存在一个如果他不存在的情况，需要考虑
        if (right == nums.length || nums[right] != target) return -1;
        return right;
    }
}

拓展和使用：

image-20210714103541557

注意，变化的是IsBlue的条件，根据要求来变化要求

细节问题

  1. 为什么left 和 right指针的初始值为-1 和 N

image-20210723110440607

  • 因为这种思路的本质是拓展或者延伸蓝红区域，所以如果数组一开始全部属于蓝色区域，则这种方法就不适用，反之依然
  1. m 是否始终处于[0,N) 内？

image-20210723111230465

  • 因为m需要始终处于数组序列中，所以一定是有意义的
  1. 更新指针时，能不能携程l=m+1, 或者r = m-1？

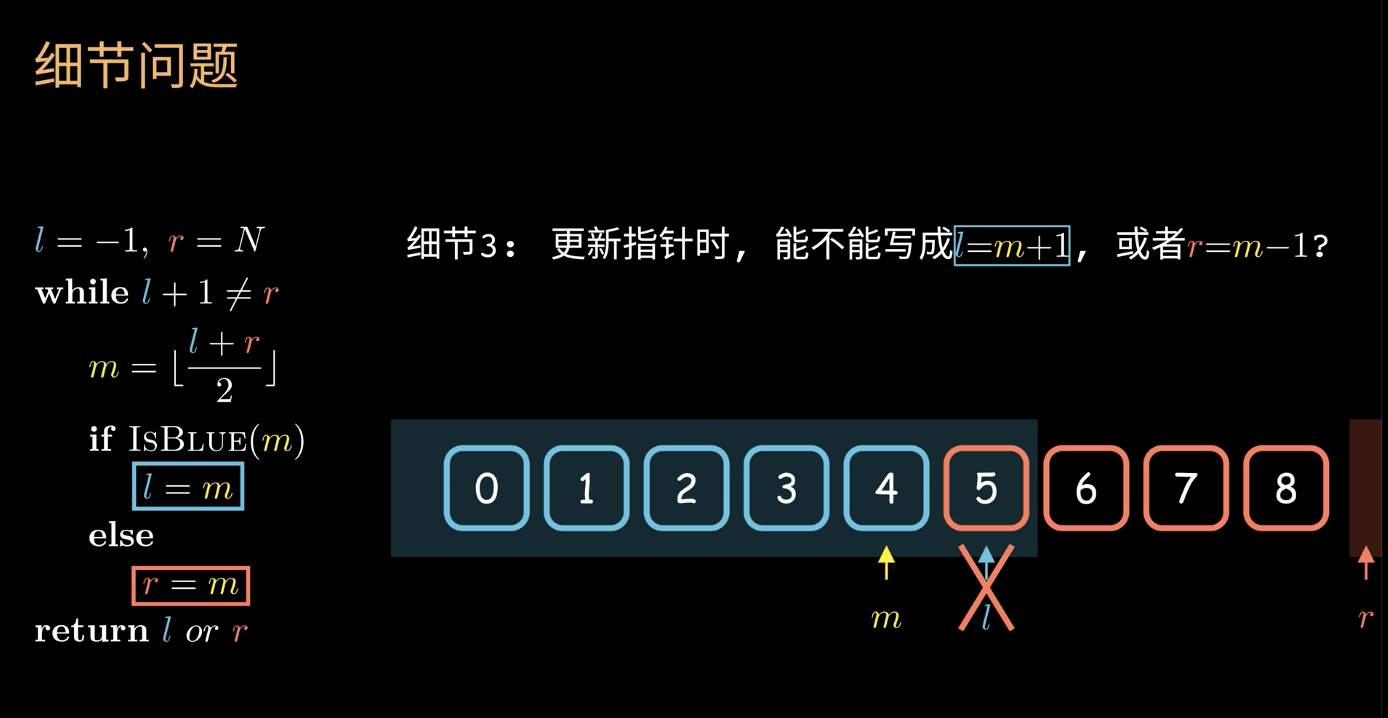
image-20210723111324873

  • 如果红蓝区域交接，如果再进行+1的操作则会是查找发现问题和错乱
  1. 程序会不会陷入死循环

image-20210723113321854

  • 无论隔了多久，他们最后的循环会退回第一种情况，然后退出循环

方法三（二分查找的另一种方式）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static int binarySearch2(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] < target) {
            left = mid+1;
        } else if (nums[mid] > target) {
            right = mid-1;
        } else {
            return mid;
        }
    }
    return -1;
}

这里需要注意的几个细节！

  • left <= right 注意是等于号，否则会死循环，就因为int是向下取整，所以一直卡着
  • 注意这里需要保证每次的更新都是下一位，一定需要+1 / -1
  • 和上一种方法不一样的是，上面的判断条件是left!=right+1

上述方法的逻辑统一

来梳理一下这些细节差异的因果逻辑：

第一个，最基本的二分查找算法：

1
2
3
4
5
6
7
8
因为我们初始化 right = nums.length - 1
所以决定了我们的「搜索区间」是 [left, right]
所以决定了 while (left <= right)
同时也决定了 left = mid+1 和 right = mid-1


因为我们只需找到一个 target 的索引即可
所以当 nums[mid] == target 时可以立即返回

第二个，寻找左侧边界的二分查找：

1
2
3
4
5
6
7
8
9
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid


因为我们需找到 target 的最左侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧右侧边界以锁定左侧边界

第三个，寻找右侧边界的二分查找：

1
2
3
4
5
6
7
8
9
10
11
12
13
因为我们初始化 right = nums.length
所以决定了我们的「搜索区间」是 [left, right)
所以决定了 while (left < right)
同时也决定了 left = mid + 1 和 right = mid


因为我们需找到 target 的最右侧索引
所以当 nums[mid] == target 时不要立即返回
而要收紧左侧边界以锁定右侧边界


又因为收紧左侧边界时必须 left = mid + 1
所以最后无论返回 left 还是 right，必须减一

对于寻找左右边界的二分搜索，常见的手法是使用左闭右开的「搜索区间」，我们还根据逻辑将「搜索区间」全都统一成了两端都闭，便于记忆，只要修改两处即可变化出三种写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
int binary_search(int[] nums, int target) {
    int left = 0, right = nums.length - 1; 
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}


int left_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }
    }
    // 最后要检查 left 越界的情况
    if (left >= nums.length || nums[left] != target)
        return -1;
    return left;
}




int right_bound(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }
    }
    // 最后要检查 right 越界的情况
    if (right < 0 || nums[right] != target)
        return -1;
    return right;
}

如果以上内容你都能理解，那么恭喜你，二分查找算法的细节不过如此。

通过本文，你学会了：

1、分析二分查找代码时，不要出现 else，全部展开成 else if 方便理解。

2、注意「搜索区间」和 while 的终止条件，如果存在漏掉的元素，记得在最后检查。

3、如需定义左闭右开的「搜索区间」搜索左右边界，只要在 nums[mid] == target 时做修改即可，搜索右侧时需要减一。

4、如果将「搜索区间」全都统一成两端都闭，好记，只要稍改 nums[mid] == target 条件处的代码和返回的逻辑即可，推荐拿小本本记下，作为二分搜索模板。

278. 第一个错误的版本

你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

示例 1：

1
2
3
4
5
6
7
输入：n = 5, bad = 4
输出：4
解释：
调用 isBadVersion(3) -> false 
调用 isBadVersion(5) -> true 
调用 isBadVersion(4) -> true
所以，4 是第一个错误的版本。

示例 2：

1
2
输入：n = 1, bad = 1
输出：1

二分查找，减少查询次数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int left = 1, right = n;
        while (left < right) { // 循环直至区间左右端点相同
            int mid = left + (right - left) / 2; // 防止计算时溢出
            if (isBadVersion(mid)) {
                right = mid; // 答案在区间 [left, mid] 中
            } else {
                left = mid + 1; // 答案在区间 [mid+1, right] 中
            }
        }
        // 此时有 left == right，区间缩为一个点，即为答案
        return left;
    }
}


35. 搜索插入位置

难度简单951

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

你可以假设数组中无重复元素。

示例 1:

1
2
输入: [1,3,5,6], 5
输出: 2

示例 2:

1
2
输入: [1,3,5,6], 2
输出: 1

示例 3:

1
2
输入: [1,3,5,6], 7
输出: 4

示例 4:

1
2
输入: [1,3,5,6], 0
输出: 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int searchInsert(int[] nums, int target) {
        int n = nums.length;
        int left = 0, right = n - 1, ans = n;
        while (left <= right) {
            int mid = ((right - left) >> 1) + left;
            if (target <= nums[mid]) {
                ans = mid;
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return ans;
    }
}


int mid = ((right - left) >> 1) + left; >>1 在这里这是什么意思

右移一位，相当于除以2，例如5的2进制表示是0101，5 >> 1以后为0010等于2，正好是5/2 = 2。如果是5 >> 2，则表示除以4，0101 右移两位之后变成 0001，正好为5/4 = 1。总的来说就是 >> 符号表示n除以2的k次方，k表示位移步数。同理<<表示左移，相当于乘以2的k次方。

1
2
3
4
5
6
7
8
9
10
11
12
13
public int searchInsert(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        int mid = 0;
        while (left <= right){
            mid = (left + right) / 2;
            if (nums[mid] < target){
                left = mid + 1;
            }else if (nums[mid] > target){
                right = mid - 1;
            }else return mid;
        }
        return nums[mid] < target ? mid + 1 : mid;
    }
  • Post title：二分查找（binary search）
  • Post author：Yuxuan Wu
  • Create time：2021-07-04 06:58:23
  • Post link：yuxuanwu17.github.io2021/07/04/2021-07-04-704.-二分查找/
  • Copyright Notice：All articles in this blog are licensed under BY-NC-SA unless stating additionally.