反转链表相关问题的集合
Yuxuan Wu Lv13
2021-06-30 02:25:23 3.7k Words 15 Mins

206. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

img

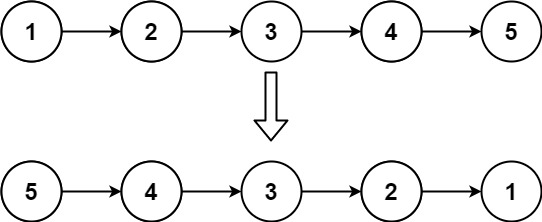
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]
示例 2：

img

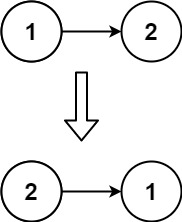
输入：head = [1,2]
输出：[2,1]
示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

进阶：链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-linked-list
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

方法1： 迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public ListNode reverseList(ListNode head) {
  // 1. 定义前指针节点和curr节点
  ListNode prev = null;
  ListNode curr = head;

  // 2.  //每次循环，都将当前节点指向它前面的节点，然后当前节点和前节点后移
  while(curr!=null){
    ListNode nextTemp = curr.next; // 临时结点，暂存当前节点的下一个节点，用于向后移位
    curr.next = prev; // 将当前节点指向他前面的一个节点，
    prev = curr;//前指针向后移动
    curr = nextTemp;//当前指针向后移动
  }
  return prev;


}

img

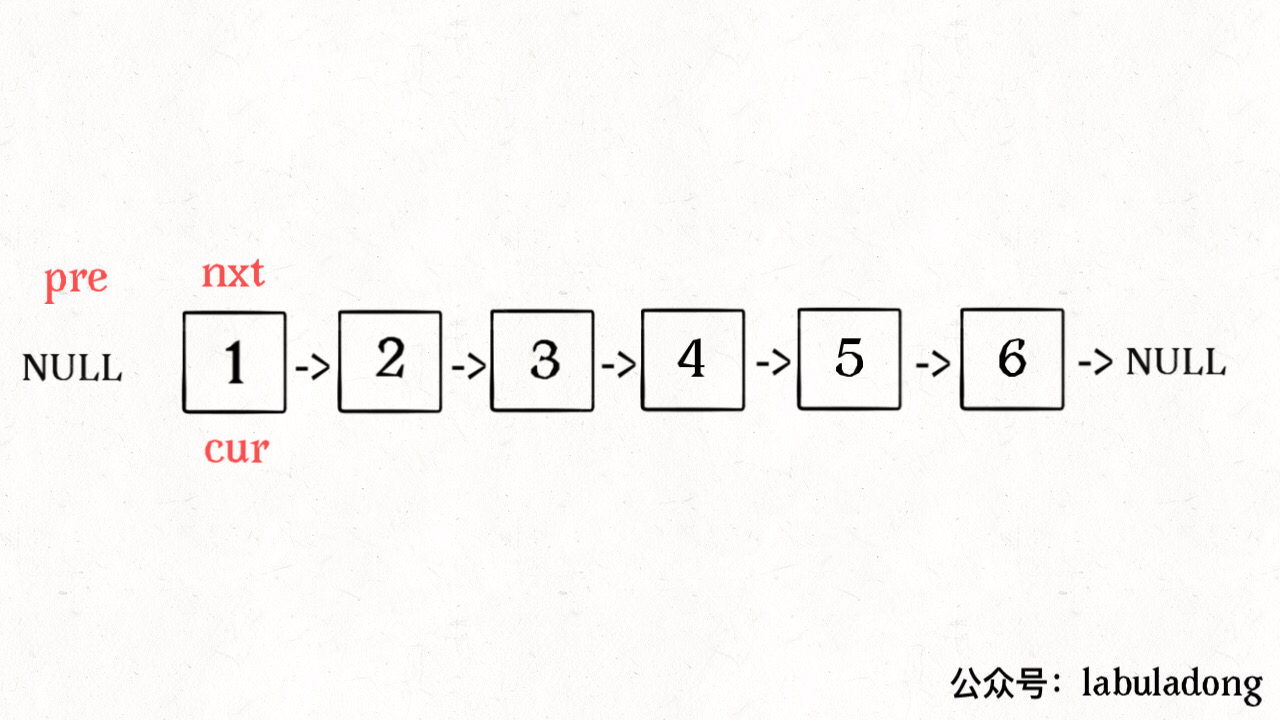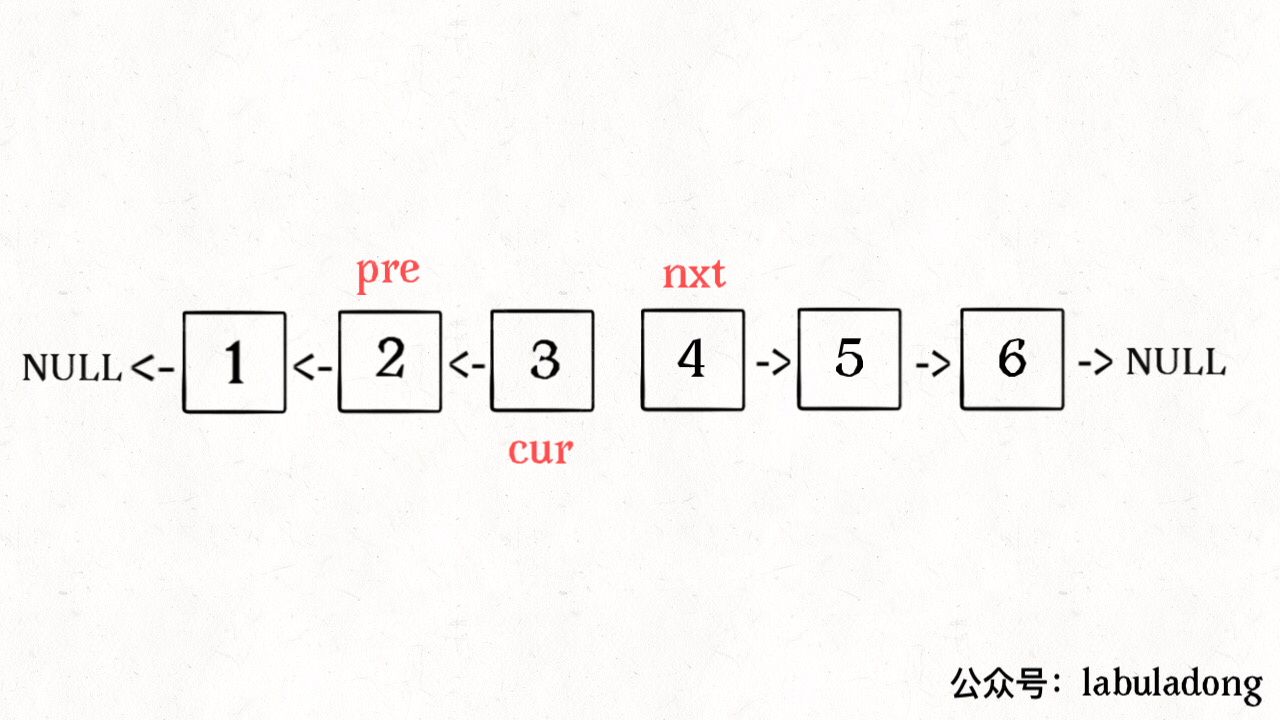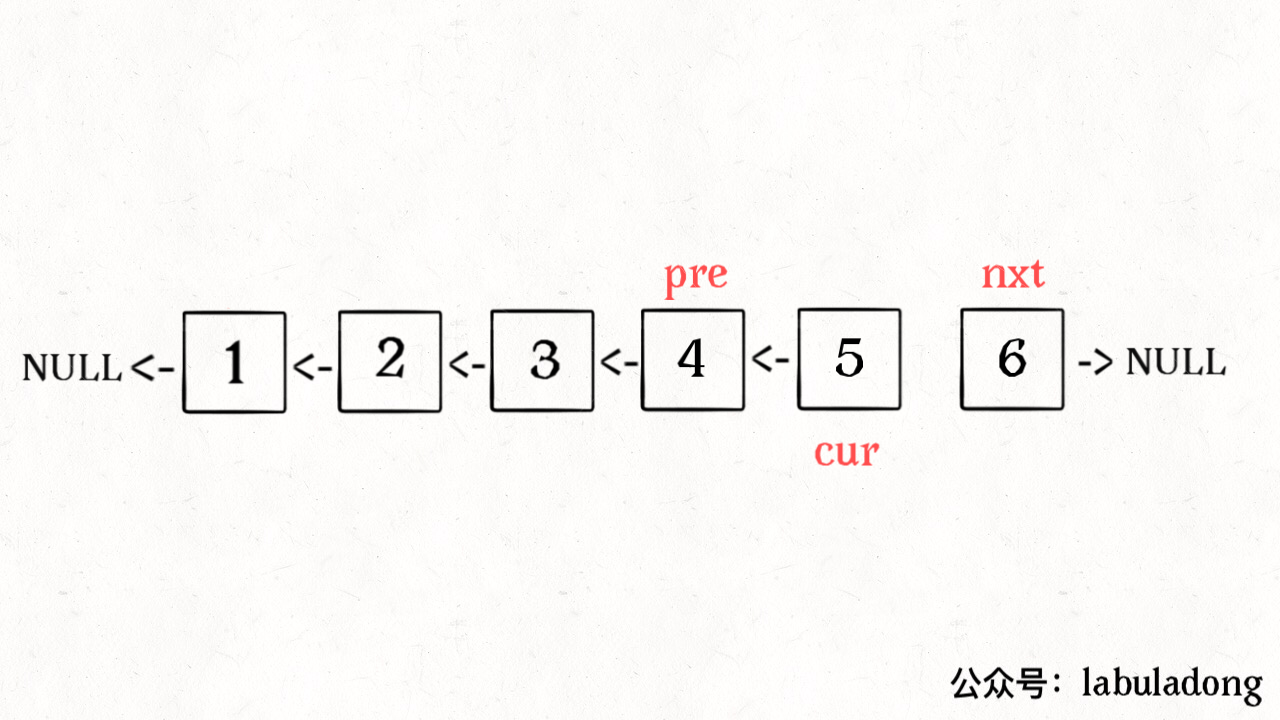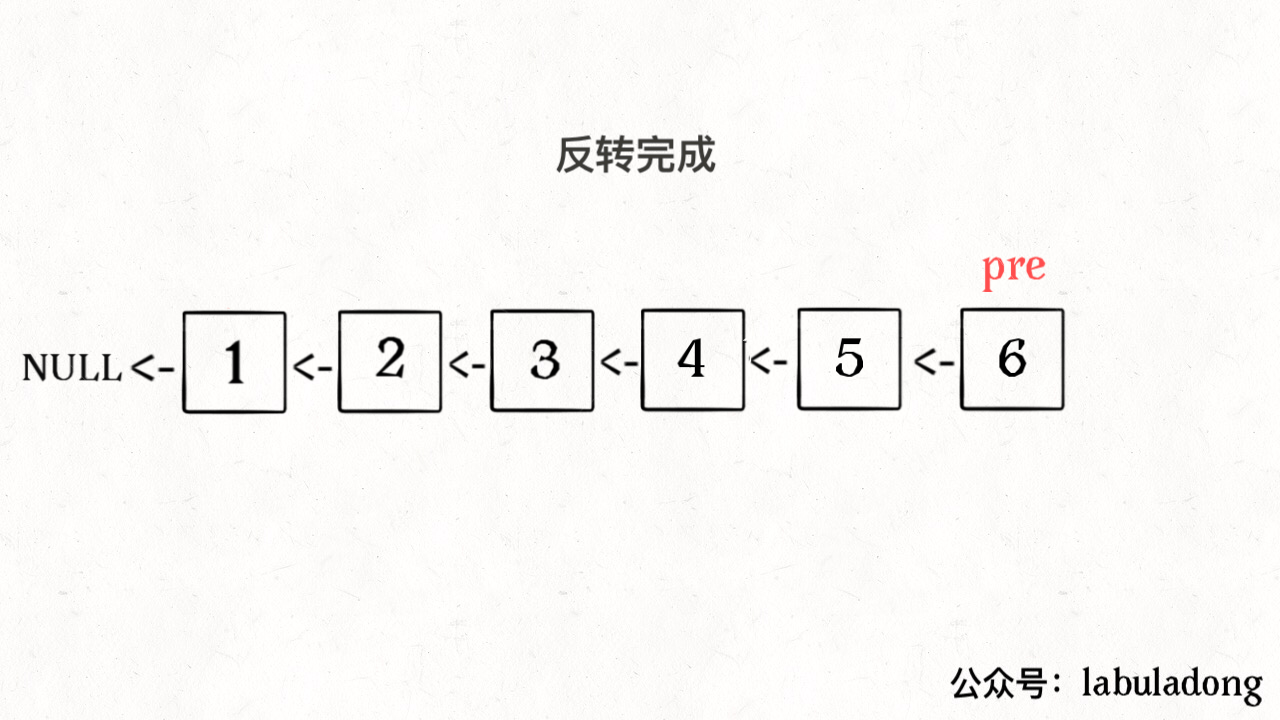
方法2:递归

为什么反转单链表可以使用递归

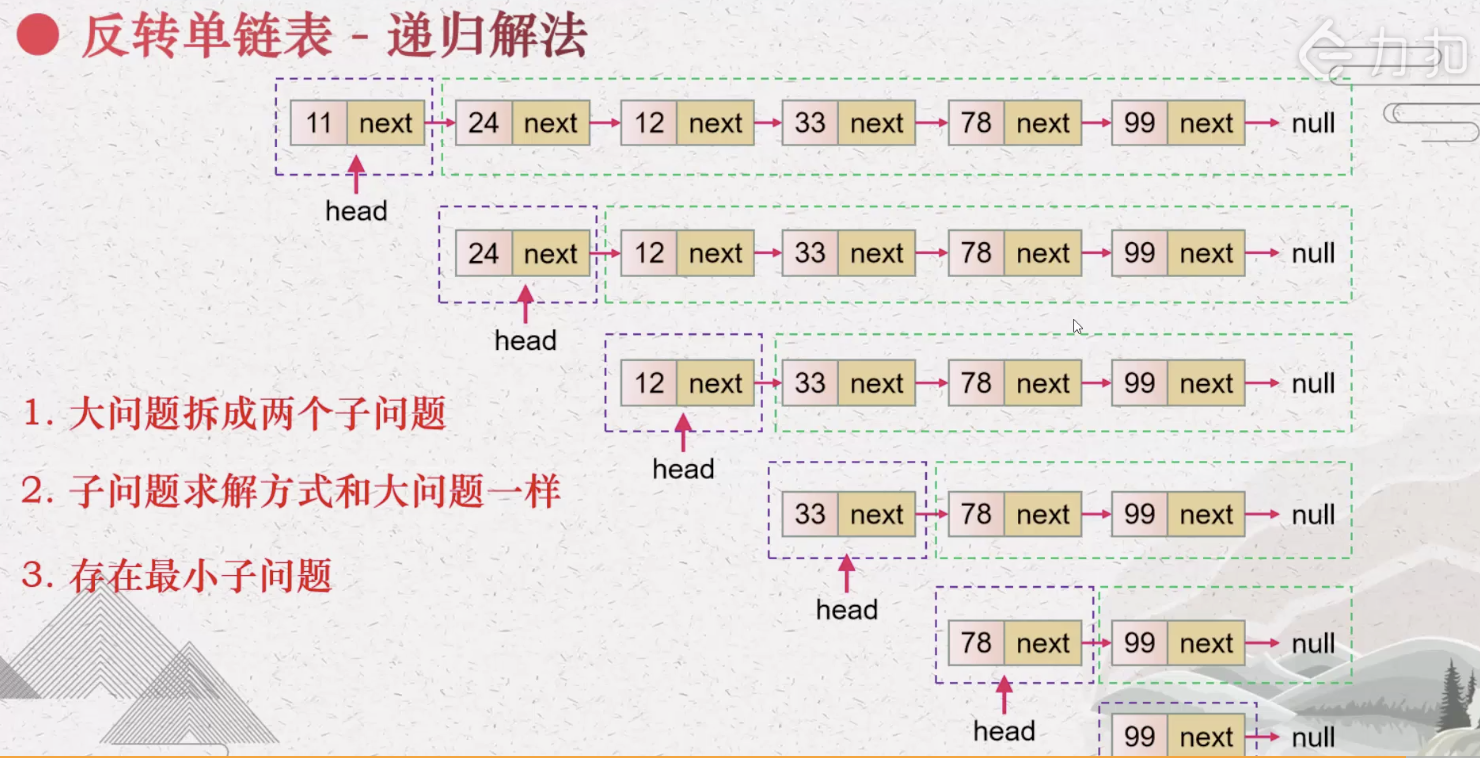
image-20210630152720383

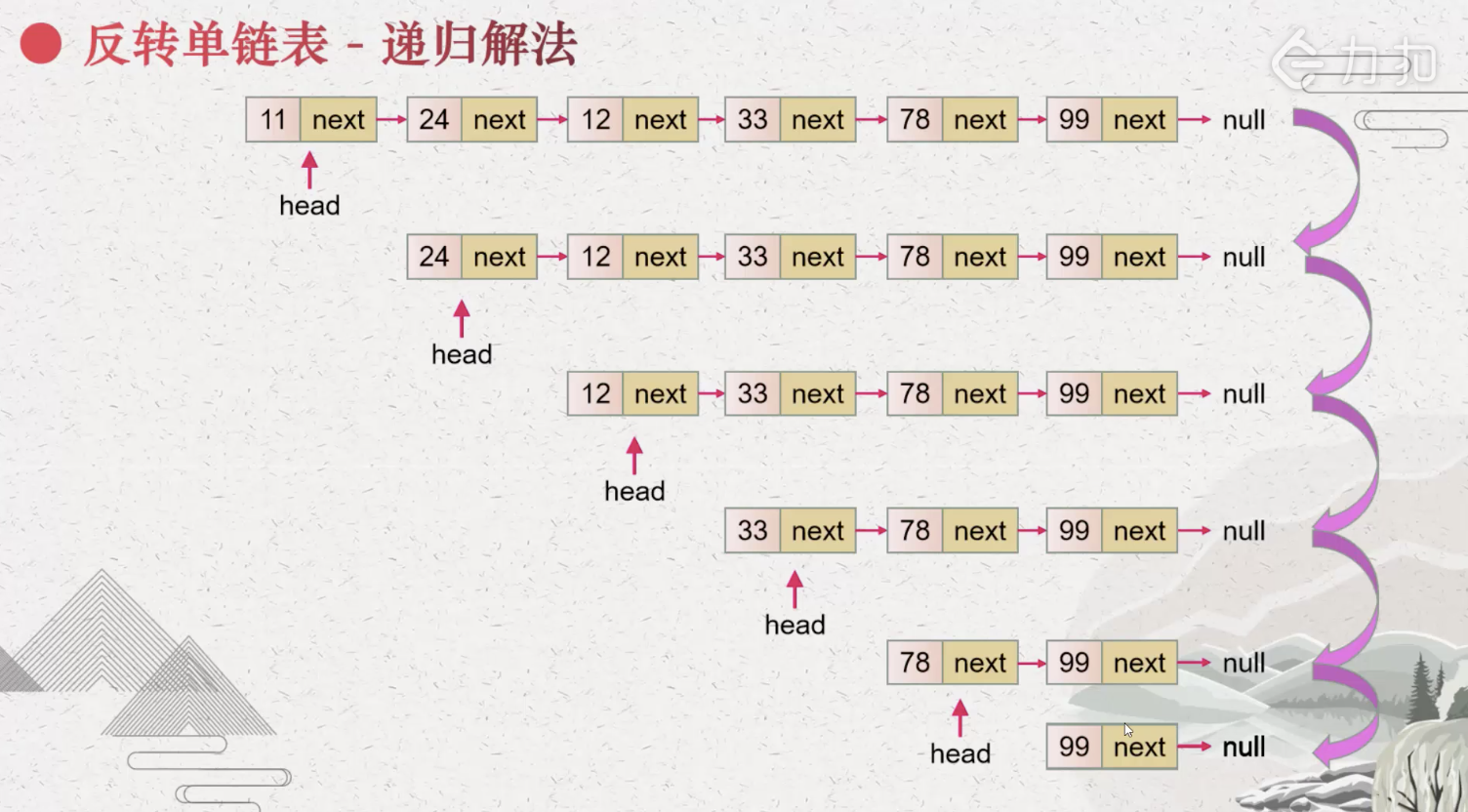
image-20210630164708719

  • 核心就是理解head.next.next=head; head.next =null 这两行代码
  • 这里递是将链表拆分为head头结点和除此之外其他的节点
  • 注意最上面的是return head 并不是直接返回答案，而是返回head节点，并用ListNode p来接受他
1
2
3
4
5
6
7
8
9
10
11
12
public ListNode reverseList2(ListNode head) {
    // 1. 先判断递归终止的条件
    // 1.1 当head==null 或者 只剩唯一一个结点，则也没有必要来进行翻转了
    // 1.2 注意返回的是head，这里是一个难以理解的点；也就是每次递归都拆分成head 和除了head以外的结点
    if (head==null||head.next==null)return head;

    // 2. 用来记录这个翻转链表 (递归递归，也是要保证移动的)
    ListNode p = reverseList2(head.next);
    head.next.next = head;
    head.next = null;
    return p;
}

递归反转整个链表（转自labuladong，侵删）

这个算法可能很多读者都听说过，这里详细介绍一下，先直接看实现代码：

1
2
3
4
5
6
7
ListNode reverse(ListNode head) {
    if (head.next == null) return head;
    ListNode last = reverse(head.next);
    head.next.next = head;
    head.next = null;
    return last;
}

看起来是不是感觉不知所云，完全不能理解这样为什么能够反转链表？这就对了，这个算法常常拿来显示递归的巧妙和优美，我们下面来详细解释一下这段代码。

对于递归算法，最重要的就是明确递归函数的定义。具体来说，我们的 reverse 函数定义是这样的：

输入一个节点 head**，将「以 **head 为起点」的链表反转，并返回反转之后的头结点。

明白了函数的定义，在来看这个问题。比如说我们想反转这个链表：

img

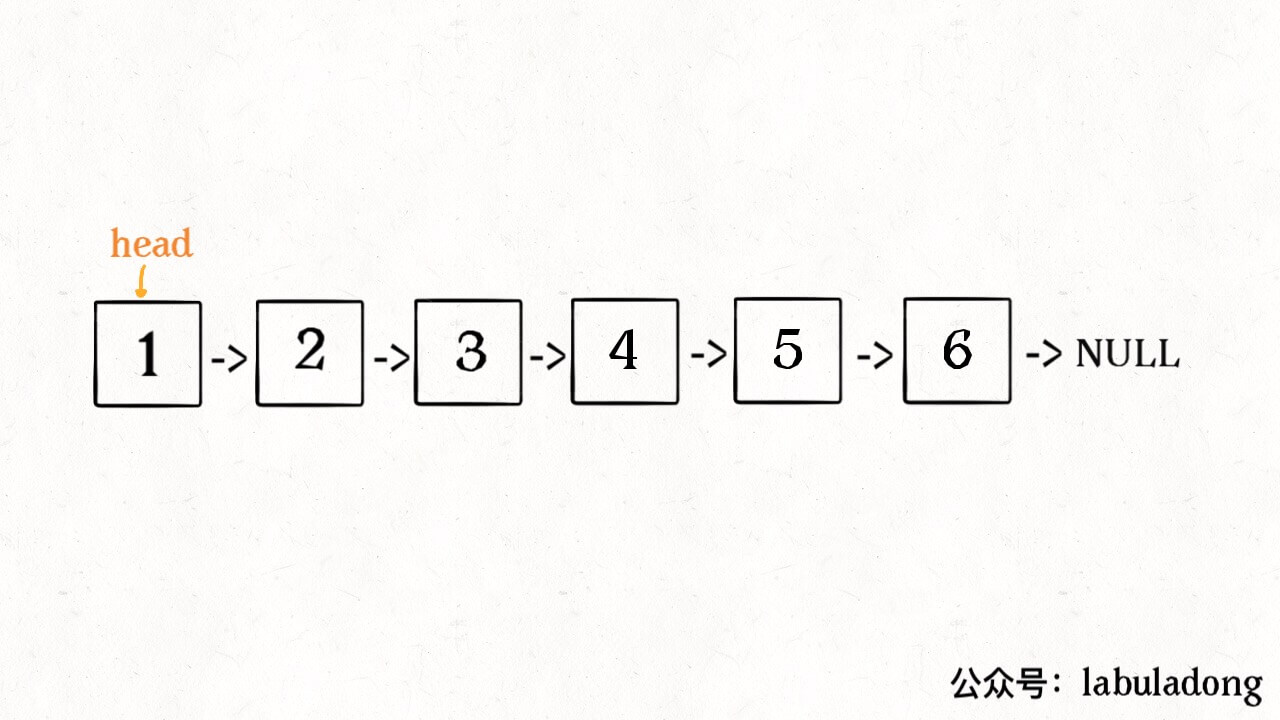
那么输入 reverse(head) 后，会在这里进行递归：

1
ListNode last = reverse(head.next);

不要跳进递归（你的脑袋能压几个栈呀？），而是要根据刚才的函数定义，来弄清楚这段代码会产生什么结果：

img

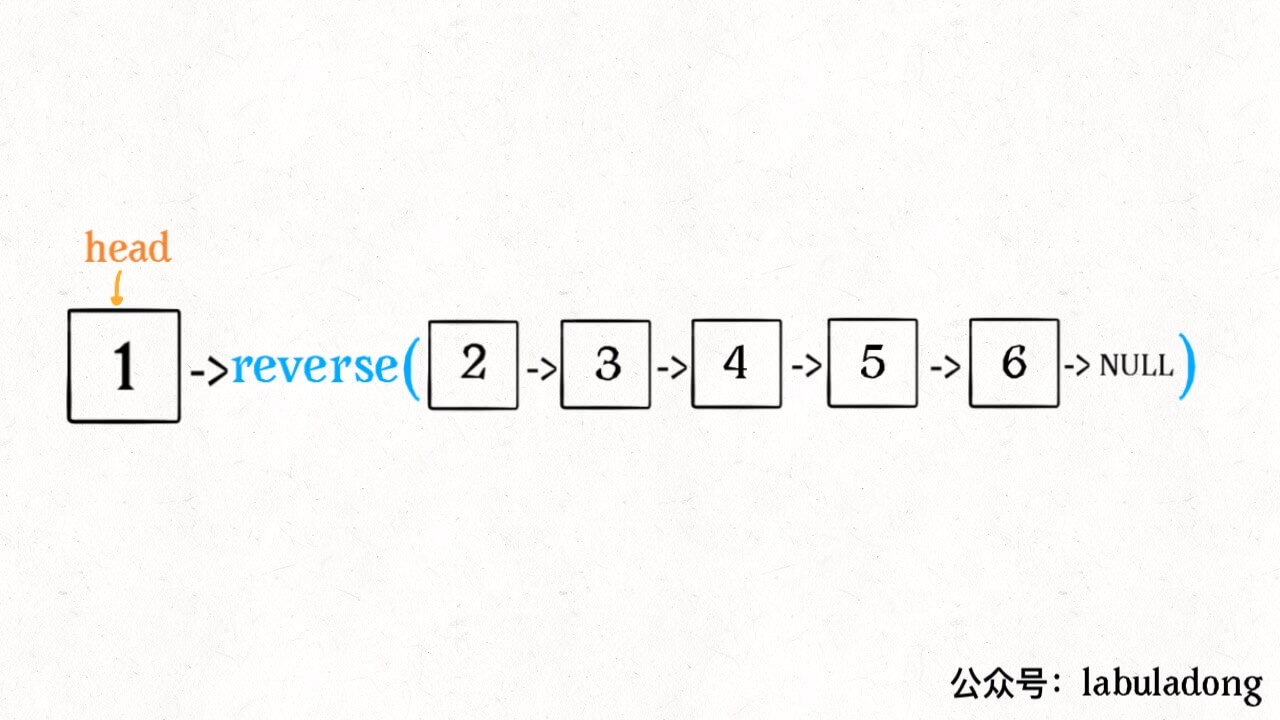
这个 reverse(head.next) 执行完成后，整个链表就成了这样：

img

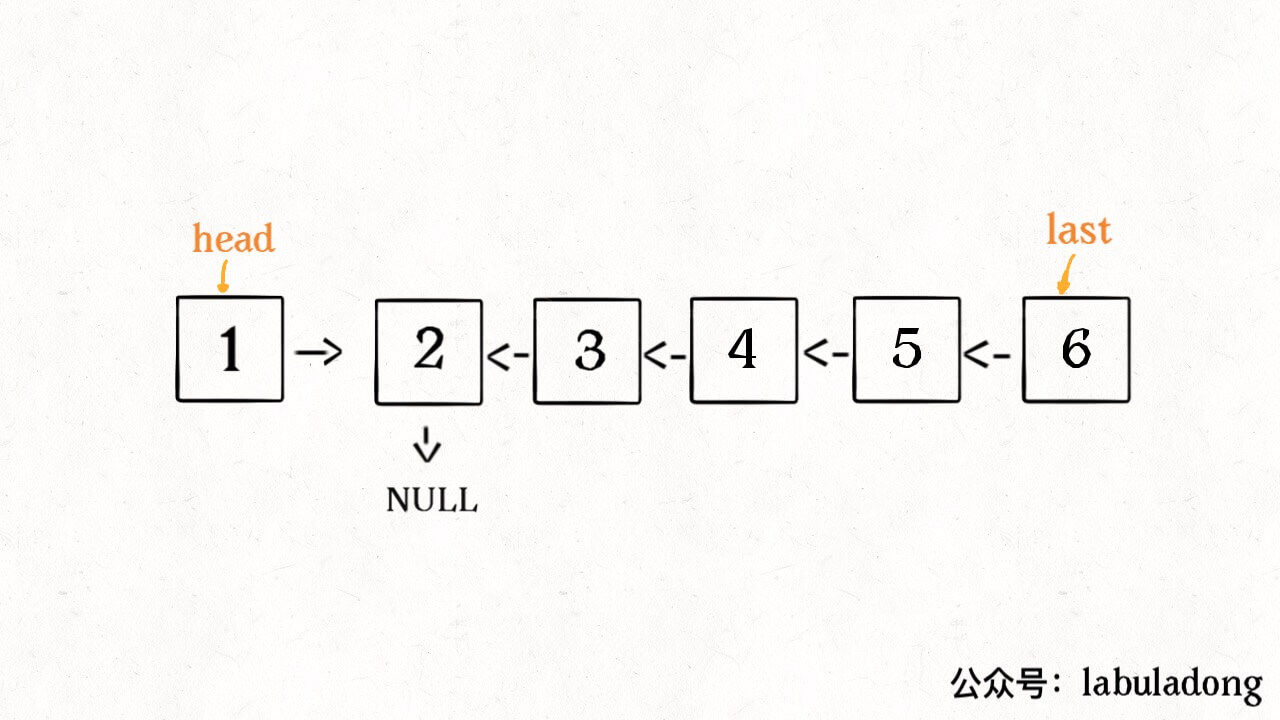
并且根据函数定义，reverse 函数会返回反转之后的头结点，我们用变量 last 接收了。

现在再来看下面的代码：

1
head.next.next = head;

img

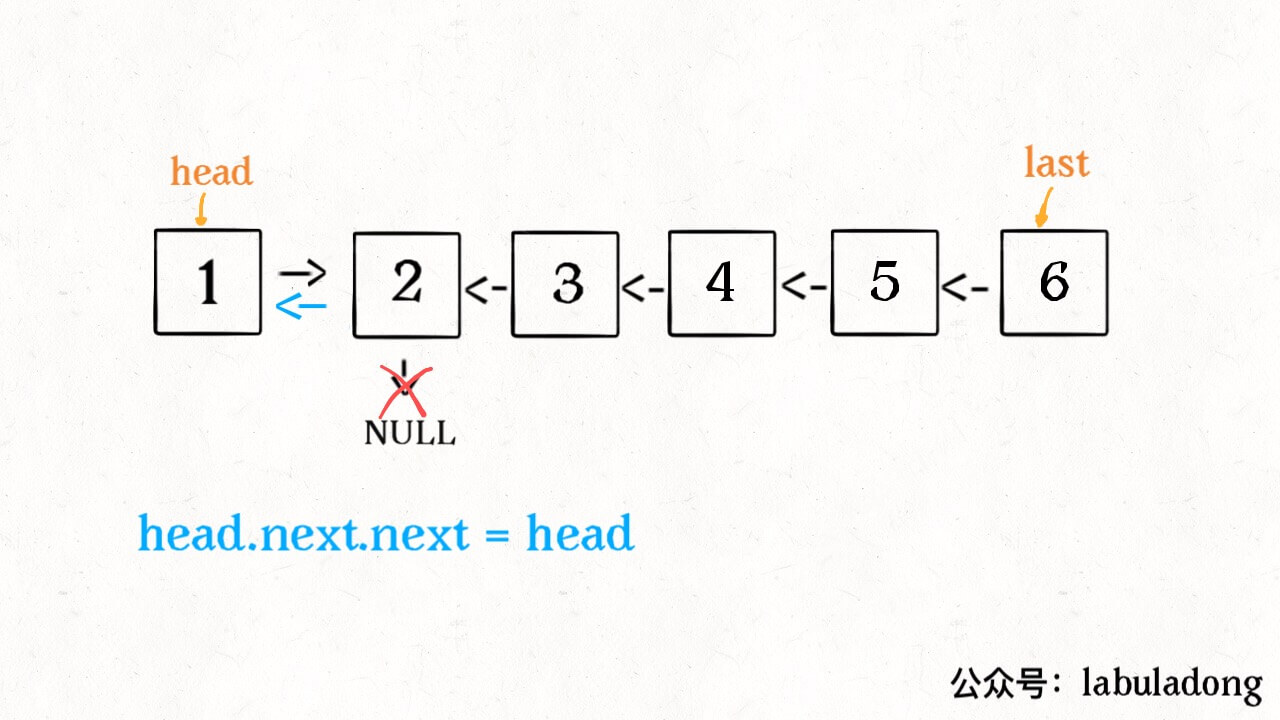
接下来：

1
2
head.next = null;
return last;

img

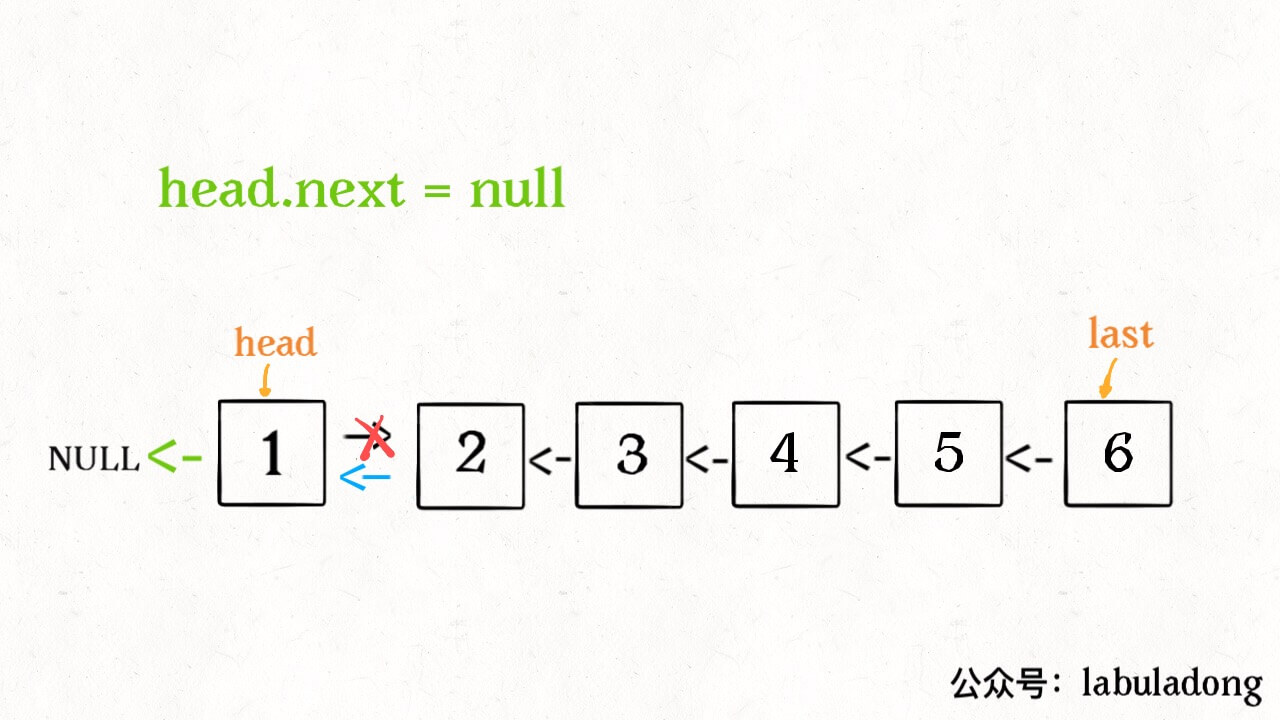
神不神奇，这样整个链表就反转过来了！递归代码就是这么简洁优雅，不过其中有两个地方需要注意：

1、递归函数要有 base case，也就是这句：

1
if (head.next == null) return head;

意思是如果链表只有一个节点的时候反转也是它自己，直接返回即可。

2、当链表递归反转之后，新的头结点是 last，而之前的 head 变成了最后一个节点，别忘了链表的末尾要指向 null：

1
head.next = null;

理解了这两点后，我们就可以进一步深入了，接下来的问题其实都是在这个算法上的扩展。

反转链表前 N 个节点

这次我们实现一个这样的函数：

1
2
// 将链表的前 n 个节点反转（n <= 链表长度）
ListNode reverseN(ListNode head, int n)

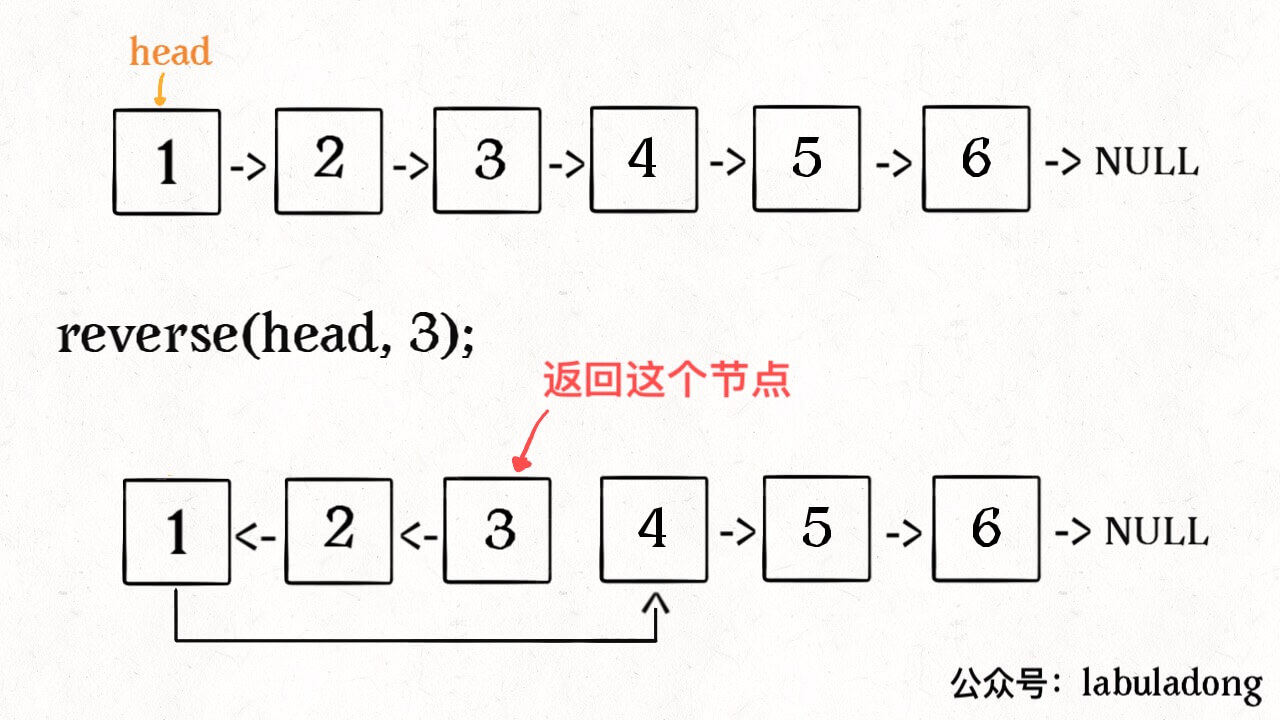
比如说对于下图链表，执行 reverseN(head, 3)：

img

解决思路和反转整个链表差不多，只要稍加修改即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
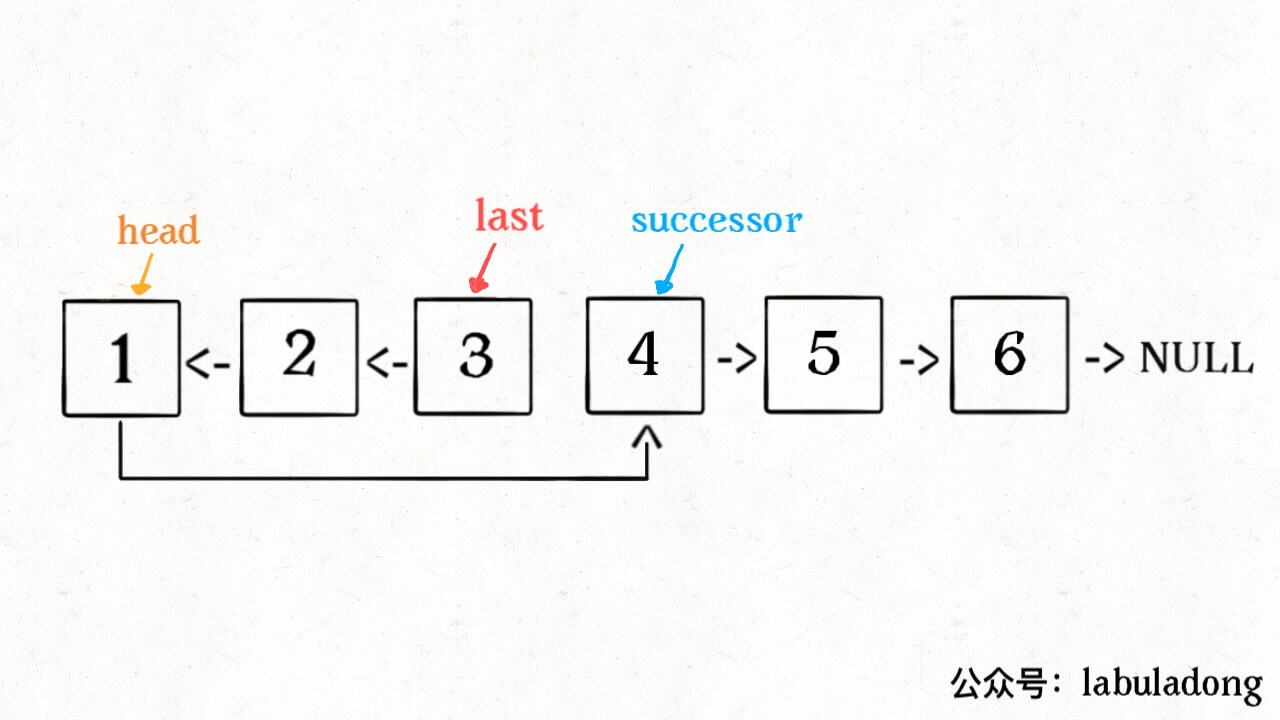
17
ListNode successor = null; // 后驱节点

// 反转以 head 为起点的 n 个节点，返回新的头结点
ListNode reverseN(ListNode head, int n) {
    if (n == 1) { 
        // 记录第 n + 1 个节点
        successor = head.next;
        return head;
    }
    // 以 head.next 为起点，需要反转前 n - 1 个节点
    ListNode last = reverseN(head.next, n - 1);

    head.next.next = head;
    // 让反转之后的 head 节点和后面的节点连起来
    head.next = successor;
    return last;
}

具体的区别：

1、base case 变为 n == 1，反转一个元素，就是它本身，同时要记录后驱节点。

2、刚才我们直接把 head.next 设置为 null，因为整个链表反转后原来的 head 变成了整个链表的最后一个节点。但现在 head 节点在递归反转之后不一定是最后一个节点了，所以要记录后驱 successor（第 n + 1 个节点），反转之后将 head 连接上。

3、值得注意的一点是进行到递归的时候successor 节点一定是定义在函数外部的，是final的，否则就会不停的覆盖原先的

img

OK，如果这个函数你也能看懂，就离实现「反转一部分链表」不远了

反转链表的一部分

现在解决我们最开始提出的问题，给一个索引区间 [m,n]（索引从 1 开始），仅仅反转区间中的链表元素。

1
ListNode reverseBetween(ListNode head, int m, int n)

首先，如果 m == 1，就相当于反转链表开头的 n 个元素嘛，也就是我们刚才实现的功能：

1
2
3
4
5
6
7
8
ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        // 相当于反转前 n 个元素
        return reverseN(head, n);
    }
    // ...
}

如果 m != 1 怎么办？如果我们把 head 的索引视为 1，那么我们是想从第 m 个元素开始反转对吧；如果把 head.next 的索引视为 1 呢？那么相对于 head.next，反转的区间应该是从第 m - 1 个元素开始的；那么对于 head.next.next 呢……

区别于迭代思想，这就是递归思想，所以我们可以完成代码：

1
2
3
4
5
6
7
8
9
ListNode reverseBetween(ListNode head, int m, int n) {
    // base case
    if (m == 1) {
        return reverseN(head, n);
    }
    // 前进到反转的起点触发 base case
    head.next = reverseBetween(head.next, m - 1, n - 1);
    return head;
}

至此，我们的最终大 BOSS 就被解决了。

具体代码的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
package linear;

public class ReverseTargetRange {

    public ListNode reverseBetween(ListNode head, int m, int n) {
        if (m == 1) {
            return reverseListN(head, n);
        }
        head.next = reverseBetween(head.next, m - 1, n - 1);
//        System.out.println("m==1 后的情况"+head);
        return head;
    }
    ListNode successor = null;
    public ListNode reverseListN(ListNode head, int num) {
        if (num == 1) {
            successor = head.next;
            return head;
        }
        ListNode last = reverseListN(head.next, num - 1);
        head.next.next = head;
        head.next = successor;
        return last;
    }
}

25. K 个一组翻转链表

给你一个链表，每 k 个节点一组进行翻转，请你返回翻转后的链表。

k 是一个正整数，它的值小于或等于链表的长度。

如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

进阶：

  • 你可以设计一个只使用常数额外空间的算法来解决此问题吗？
  • 你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

img

1
2
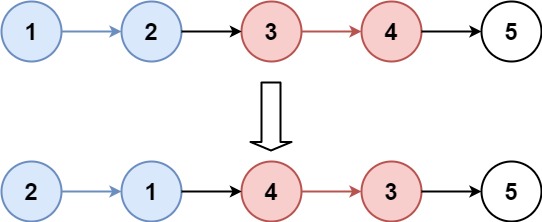
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

img

1
2
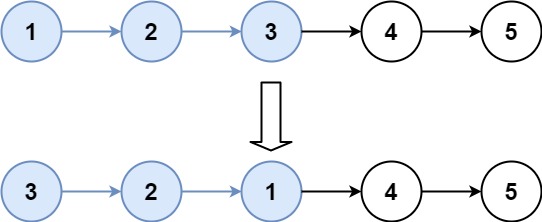
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

示例 3：

1
2
输入：head = [1,2,3,4,5], k = 1
输出：[1,2,3,4,5]

示例 4：

1
2
输入：head = [1], k = 1
输出：[1]

思路题解：

  1. 之前已经可以用迭代的方式来反转整个链表

  2. 「反转以 a 为头结点的链表」其实就是「反转 a 到 null 之间的结点」，那么如果让你「反转 a 到 b 之间的结点」，你会不会？

    只要更改函数签名，并把上面的代码中 null 改成 b 即可：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    /** 反转区间 [a, b) 的元素，注意是左闭右开 */
    ListNode reverse(ListNode a, ListNode b) {
        ListNode pre, cur, nxt;
        pre = null; cur = a; nxt = a;
        // while 终止的条件改一下就行了
        while (cur != b) {
            nxt = cur.next;
            cur.next = pre;
            pre = cur;
            cur = nxt;
        }
        // 返回反转后的头结点
        return pre;
    }

现在我们迭代实现了反转部分链表的功能，接下来就按照之前的逻辑编写 reverseKGroup 函数即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode reverseKGroup(ListNode head, int k) {
    if (head == null) return null;
    // 区间 [a, b) 包含 k 个待反转元素
    ListNode a, b;
    a = b = head;
    for (int i = 0; i < k; i++) {
        // 不足 k 个，不需要反转，base case
        if (b == null) return head;
        b = b.next;
    }
    // 反转前 k 个元素
    ListNode newHead = reverse(a, b);
    // 递归反转后续链表并连接起来
    a.next = reverseKGroup(b, k);
    return newHead;
}

解释一下 for 循环之后的几句代码，注意 reverse 函数是反转区间 [a, b)，所以情形是这样的：

img

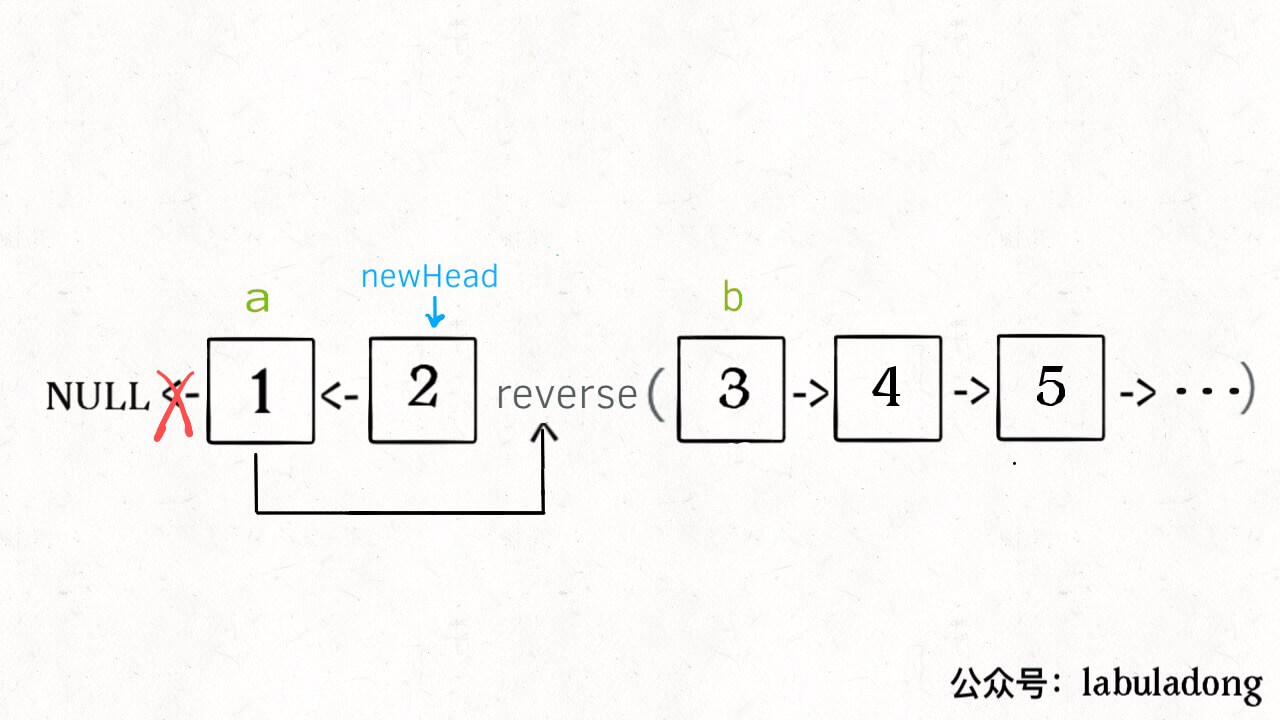
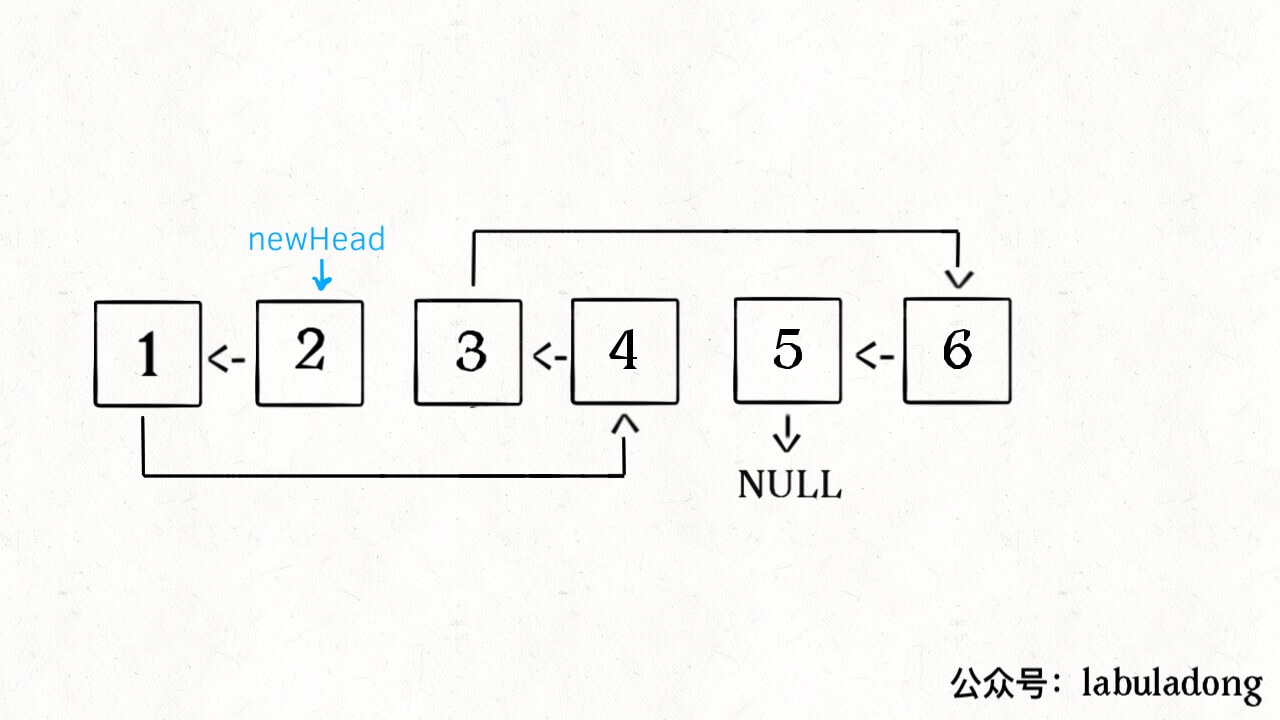
递归部分就不展开了，整个函数递归完成之后就是这个结果，完全符合题意：

img

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
package linear;

public class ReverseKGroup {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null) return null;
        ListNode a = head;
        ListNode b = head;

        for (int i = 0; i < k; i++) {
            // base case 是不足k，就不需要反转
            if (b == null) return head;
            b = b.next;
        }
        ListNode newNode = reverse(a, b);
        a.next = reverseKGroup(b, k);

        return newNode;
    }

    public ListNode reverse(ListNode a, ListNode b) {
        ListNode prev, curr, nxt;
        prev = null;
        curr = a;
        while (curr != b) {
            nxt = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nxt;
        }

        return prev;

    }
}

234. 回文链表

难度简单1073

请判断一个链表是否为回文链表。

示例 1:

1
2
输入: 1->2
输出: false

示例 2:

1
2
输入: 1->2->2->1
输出: true

这道题的关键在于，单链表无法倒着遍历，无法使用双指针技巧。那么最简单的办法就是，把原始链表反转存入一条新的链表，然后比较这两条链表是否相同。关于如何反转链表，可以参见前文 递归翻转链表的一部分。

其实，借助二叉树后序遍历的思路，不需要显式反转原始链表也可以倒序遍历链表，下面来具体聊聊。

对于二叉树的几种遍历方式，我们再熟悉不过了：

1
2
3
4
5
6
7
void traverse(TreeNode root) {
    // 前序遍历代码
    traverse(root.left);
    // 中序遍历代码
    traverse(root.right);
    // 后序遍历代码
}

在「学习数据结构的框架思维」中说过，链表兼具递归结构，树结构不过是链表的衍生。那么，链表其实也可以有前序遍历和后序遍历：

1
2
3
4
5
void traverse(ListNode head) {
    // 前序遍历代码
    traverse(head.next);
    // 后序遍历代码
}

这个框架有什么指导意义呢？如果我想正序打印链表中的val值，可以在前序遍历位置写代码；反之，如果想倒序遍历链表，就可以在后序遍历位置操作：

1
2
3
4
5
6
7
/* 倒序打印单链表中的元素值 */
void traverse(ListNode head) {
    if (head == null) return;
    traverse(head.next);
    // 后序遍历代码
    print(head.val);
}

说到这了，其实可以稍作修改，模仿双指针实现回文判断的功能：

用arrayList来存储

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean isPalindrome(ListNode head) {

        ArrayList<Integer> node1 = nodeToArray(head);
        ListNode reverseListNode = traverse(head);
        ArrayList<Integer> node2 = nodeToArray(reverseListNode);
        return node1.equals(node2);
    }

    public ArrayList<Integer> nodeToArray(ListNode head) {
        ArrayList<Integer> node = new ArrayList<>();
        while (head != null) {
            node.add(head.val);
            head = head.next;
        }
        return node;
    }

    public ListNode traverse(ListNode head) {
        if (head == null || head.next == null) return head;
      	ListNode last = traverse(head.next);
        head.next.next = head;
        head.next = null;
        return last;
    }
}
  1. 翻转链表
  2. ListNode转换成ArrayList并且储存
  3. 判断两者的值是否相等

双指针堆栈思想

这么做的核心逻辑是什么呢？实际上就是把链表节点放入一个栈，然后再拿出来，这时候元素顺序就是反的，只不过我们利用的是递归函数的堆栈而已。

1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
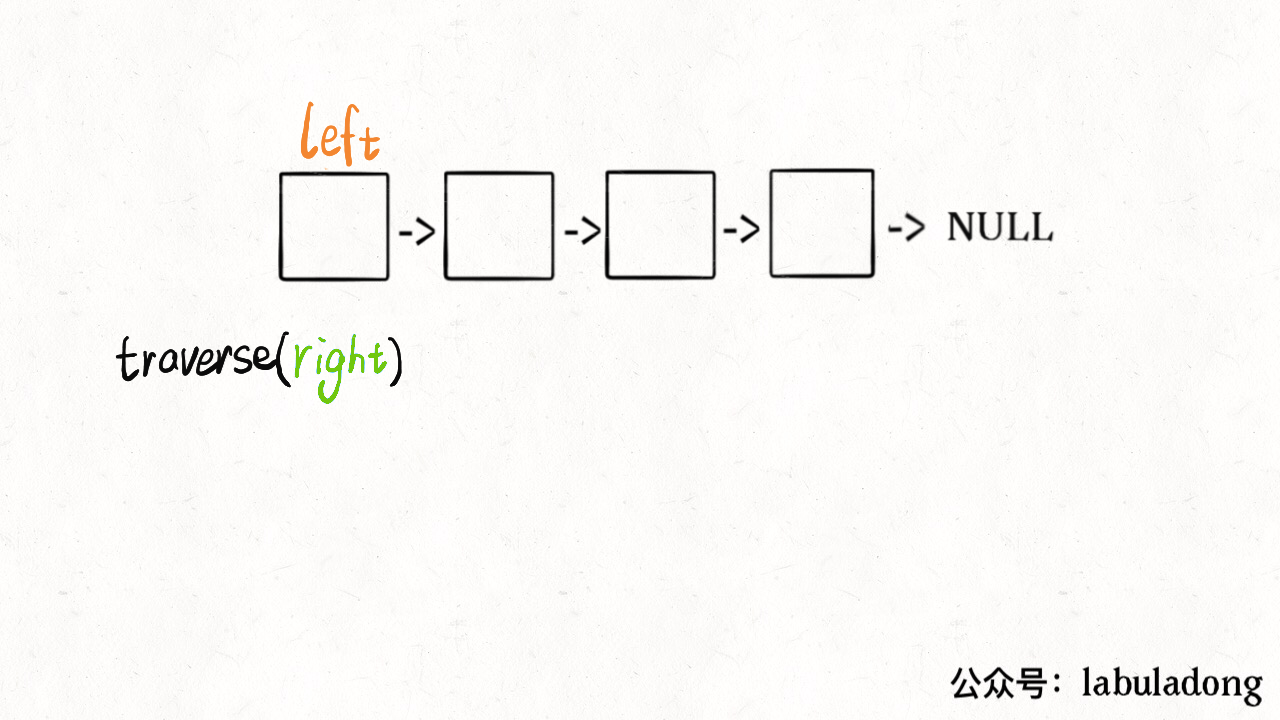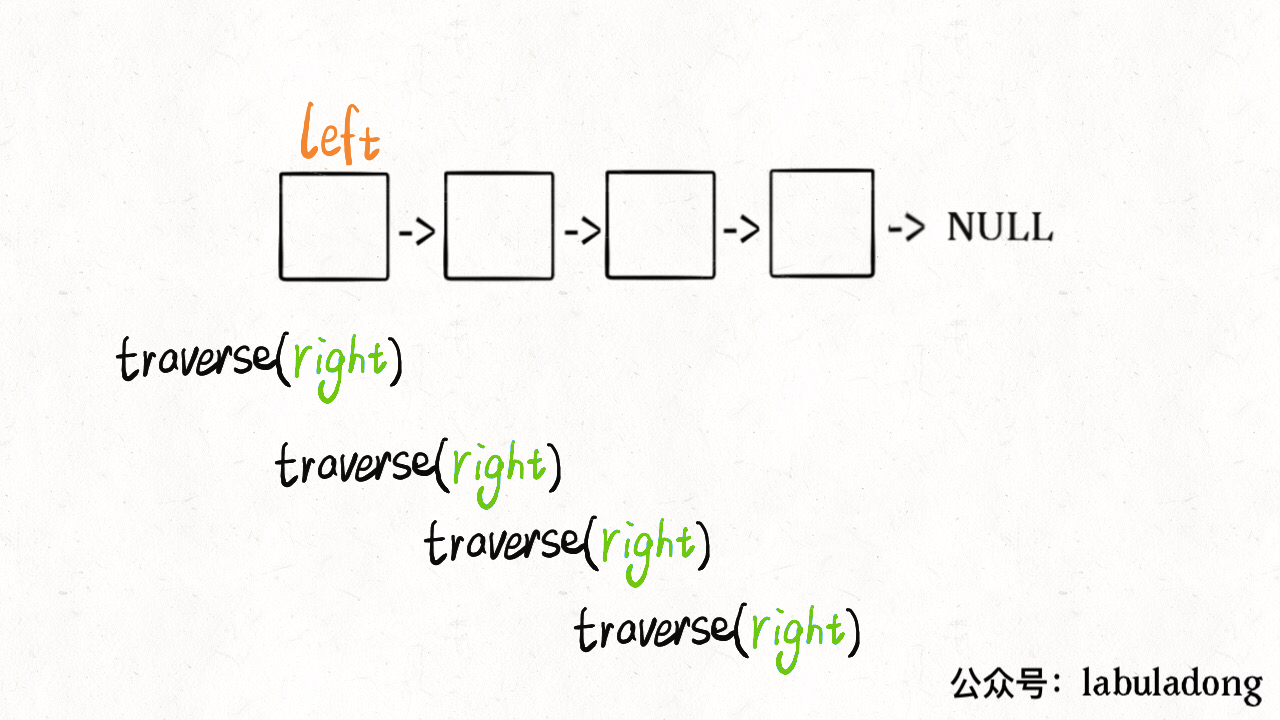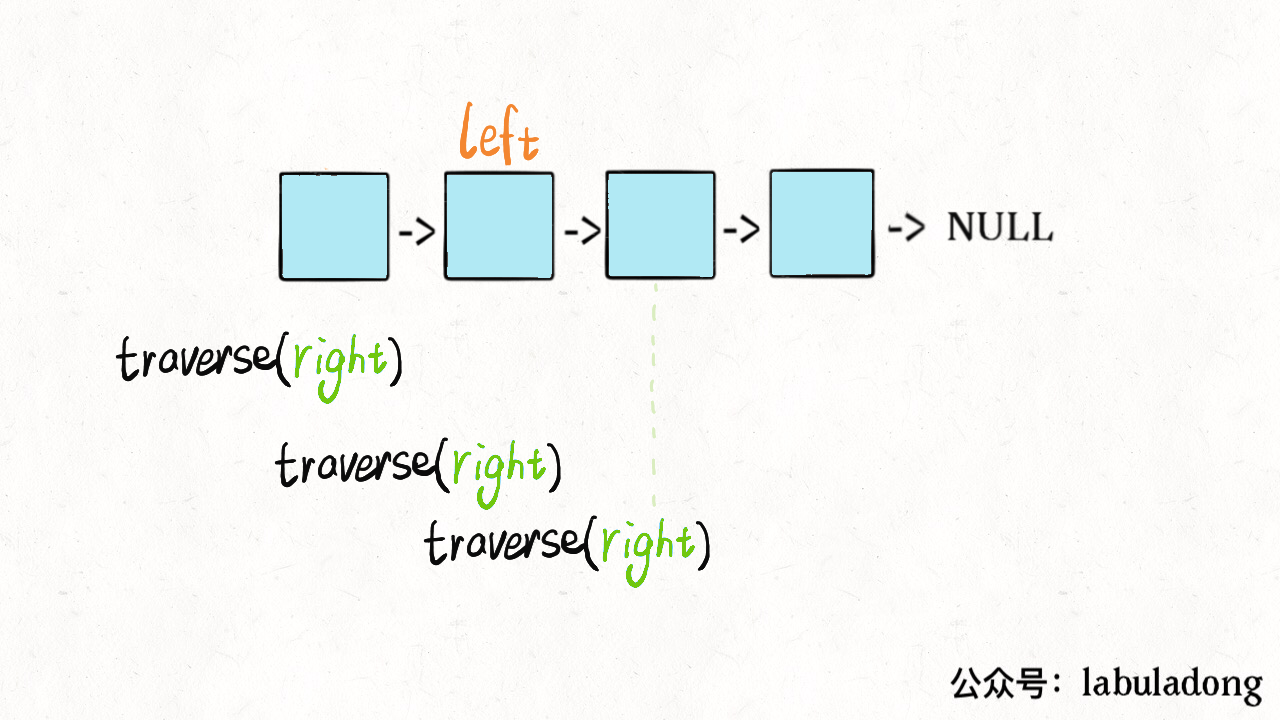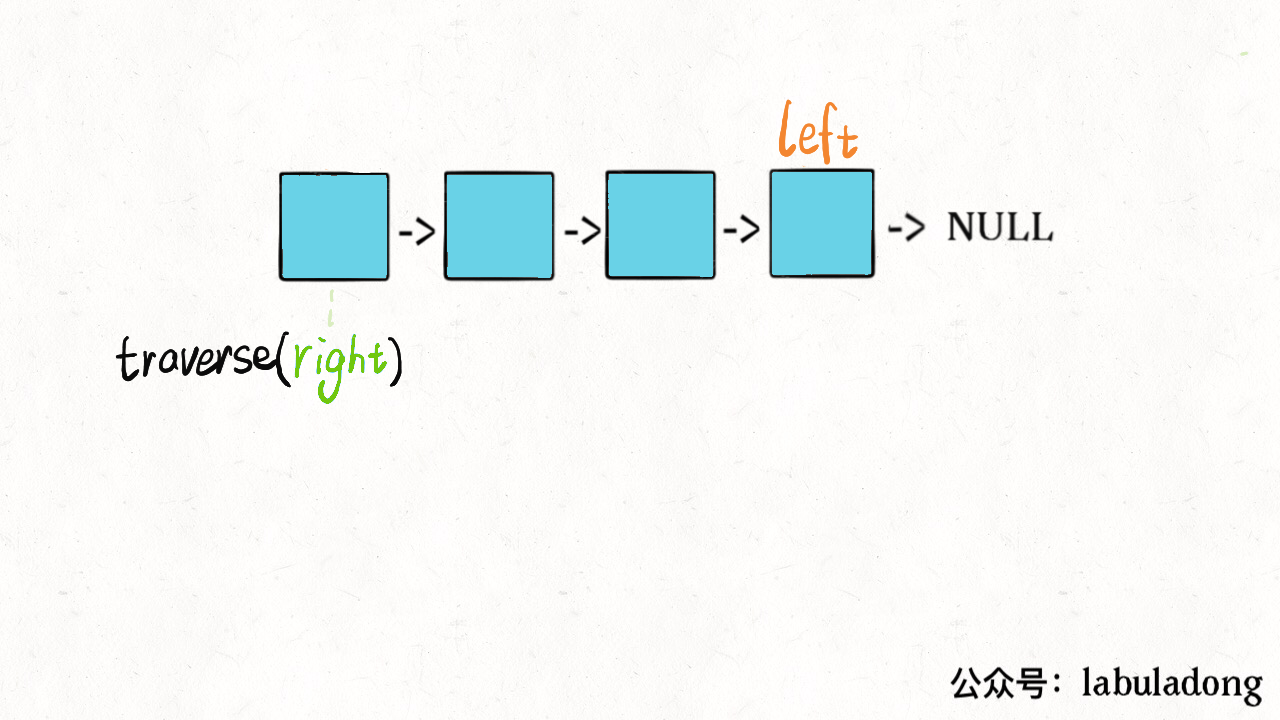
17
class Solution {
    ListNode left;
    public boolean isPalindrome(ListNode head) {
        left = head;
        return traverse(head);

    }

    public boolean traverse(ListNode right){
        if(right==null) return true;
        boolean res = traverse(right.next);
        res = res && (right.val == left.val);
        left = left.next;
        return res;

    }
}

当然，无论造一条反转链表还是利用后序遍历，算法的时间和空间复杂度都是 O(N)。下面我们想想，能不能不用额外的空间，解决这个问题呢？

二、优化空间复杂度

更好的思路是这样的：

1、先通过「双指针技巧」中的快慢指针来找到链表的中点：

1
2
3
4
5
6
7
ListNode slow, fast;
slow = fast = head;
while (fast != null && fast.next != null) {
    slow = slow.next;
    fast = fast.next.next;
}
// slow 指针现在指向链表中点

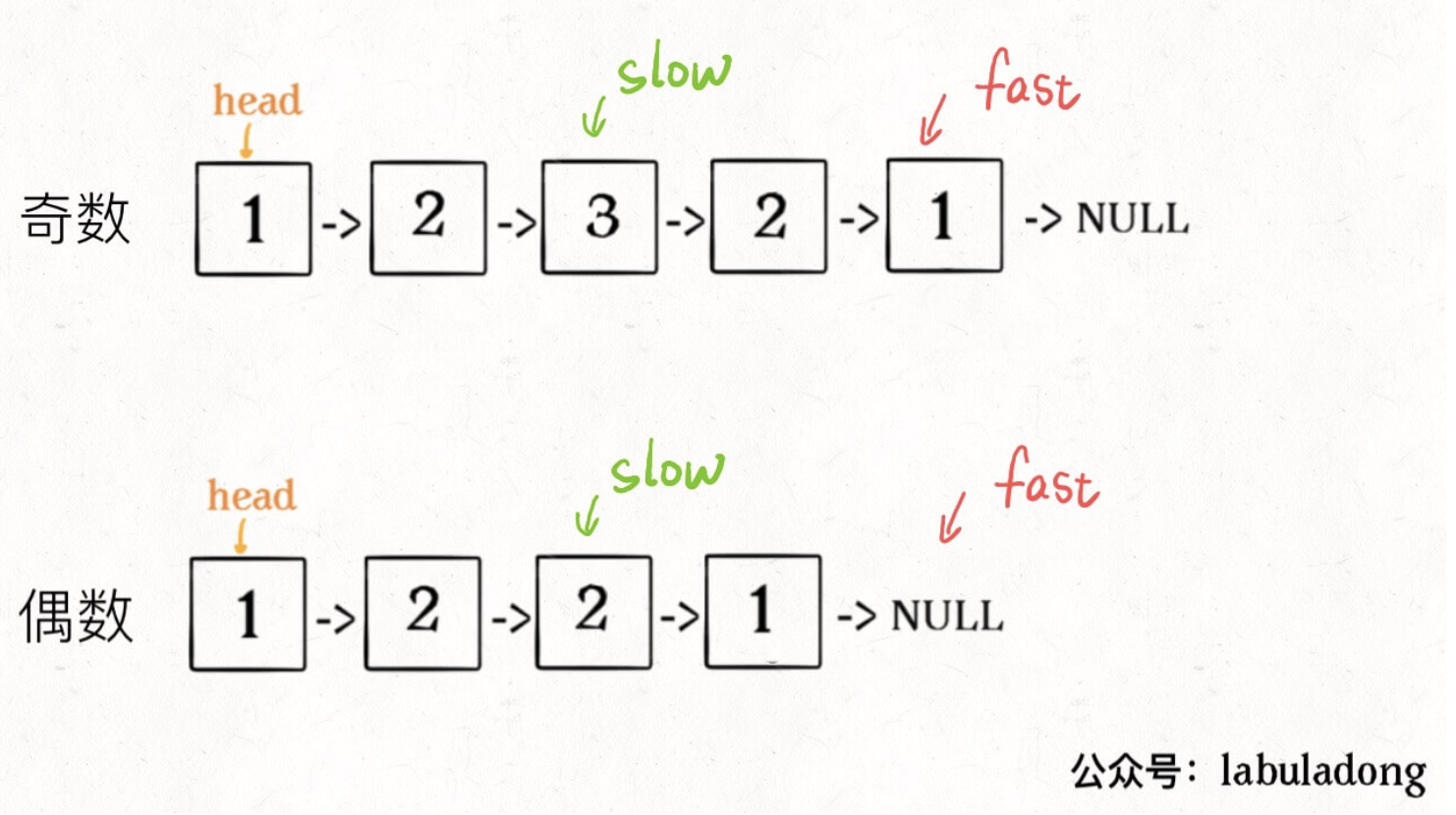
image-20210809153903320

2、如果**fast指针没有指向null，说明链表长度为奇数，slow**还要再前进一步：

1
2
if (fast != null)
    slow = slow.next;

2

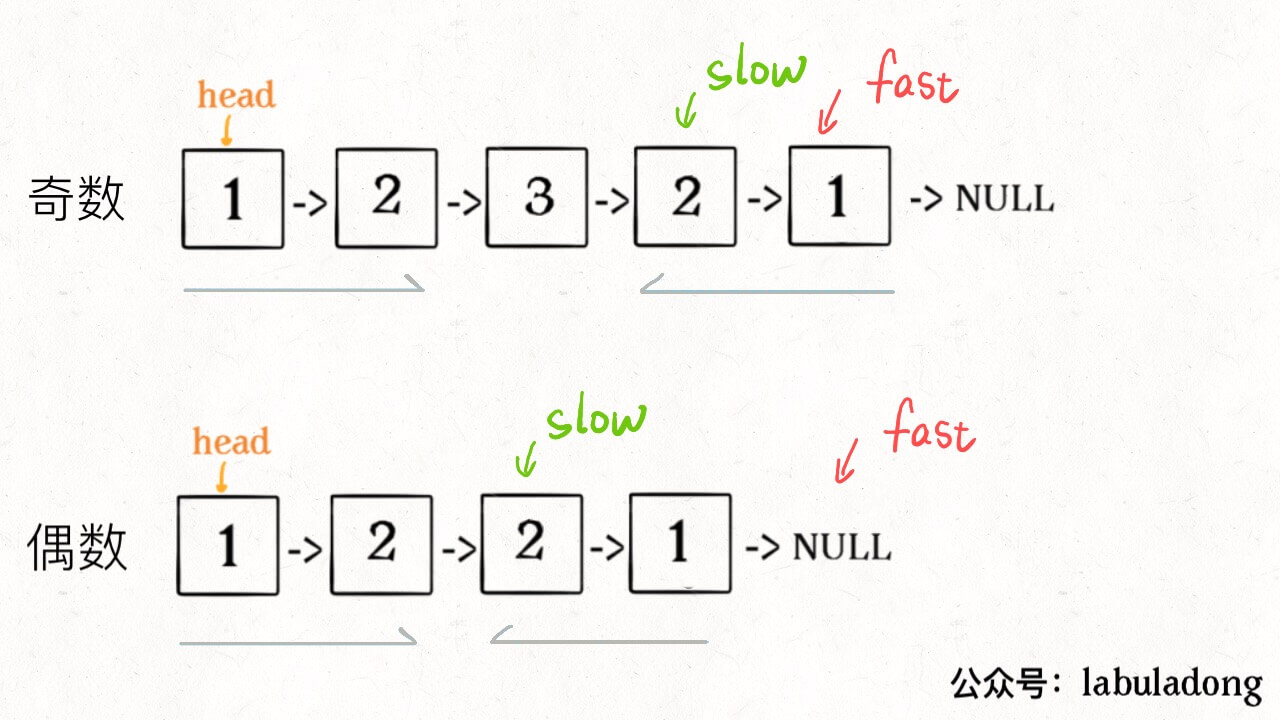
3、从**slow**开始反转后面的链表，现在就可以开始比较回文串了：

1
2
3
4
5
6
7
8
9
10
ListNode left = head;
ListNode right = reverse(slow);

while (right != null) {
    if (left.val != right.val)
        return false;
    left = left.next;
    right = right.next;
}
return true;

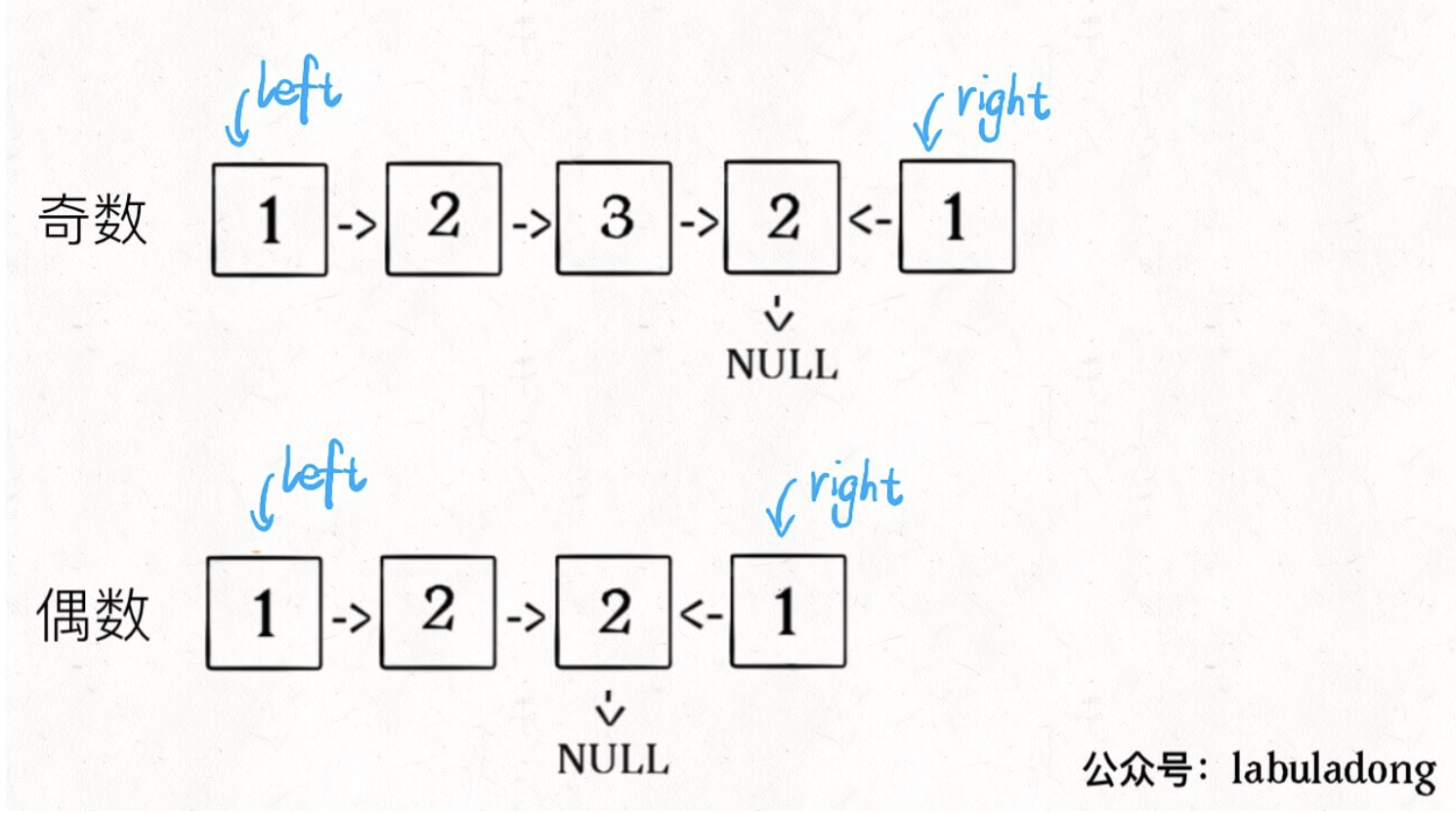
image-20210809153956688

至此，把上面 3 段代码合在一起就高效地解决这个问题了，其中reverse函数很容易实现：

1
2
3
4
5
6
7
8
9
10
ListNode reverse(ListNode head) {
    ListNode pre = null, cur = head;
    while (cur != null) {
        ListNode nxt = cur.next;
        cur.next = pre;
        pre = cur;
        cur = nxt;
    }
    return pre;
}

img

算法总体的时间复杂度 O(N)，空间复杂度 O(1)，已经是最优的了。

我知道肯定有读者会问：这种解法虽然高效，但破坏了输入链表的原始结构，能不能避免这个瑕疵呢？

其实这个问题很好解决，关键在于得到p, q这两个指针位置：

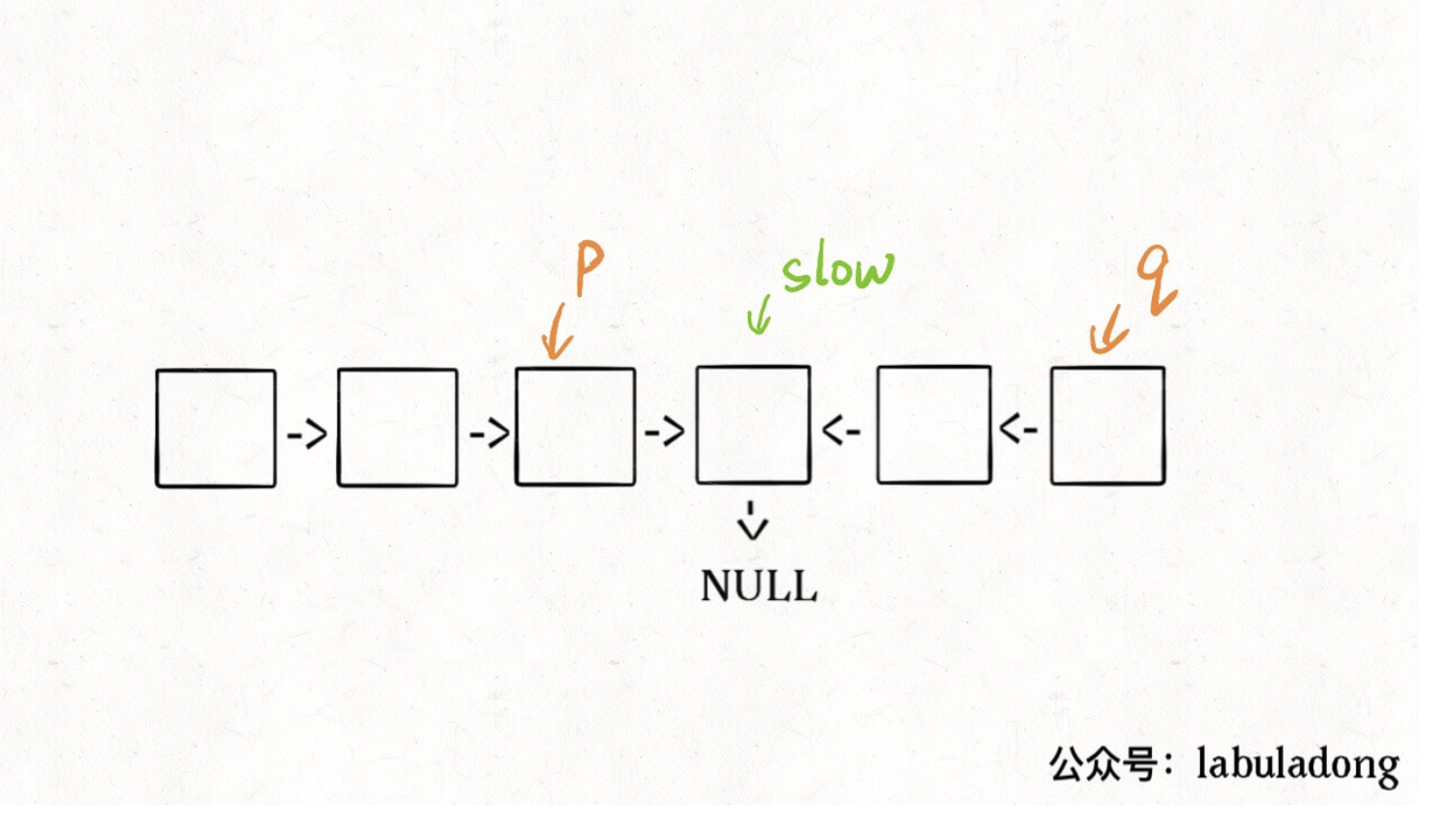
image-20210809155544978

这样，只要在函数 return 之前加一段代码即可恢复原先链表顺序：

1
p.next = reverse(q);

篇幅所限，我就不写了，读者可以自己尝试一下。

完整的java代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public boolean isPalindrome(ListNode head) {
       ListNode slow = findMiddleNode(head);
        ListNode left = head;
        ListNode right = traverse(slow);

        while (right != null) {
            if (left.val != right.val) {
                return false;
            }
            left = left.next;
            right = right.next;
        }
        return true;

    }

    public ListNode findMiddleNode(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;

        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }

        if (fast != null)
            slow = slow.next;
        return slow;
    }
        public ListNode traverse(ListNode head) {
        if (head == null || head.next == null) return head;

        ListNode last = traverse(head.next);
        head.next.next = head;
        head.next = null;
        return last;
    }
}
  • Post title：反转链表相关问题的集合
  • Post author：Yuxuan Wu
  • Create time：2021-06-30 02:25:23
  • Post link：yuxuanwu17.github.io2021/06/30/2021-06-30-206.-反转链表/
  • Copyright Notice：All articles in this blog are licensed under BY-NC-SA unless stating additionally.