小结 - 链表中的双指针

在这里，我们为你提供了一个模板，用于解决链表中的双指针问题。

// Initialize slow & fast pointers
ListNode slow = head;
ListNode fast = head;
/**
 * Change this condition to fit specific problem.
 * Attention: remember to avoid null-pointer error
 **/
while (slow != null && fast != null && fast.next != null) {
    slow = slow.next;           // move slow pointer one step each time
    fast = fast.next.next;      // move fast pointer two steps each time
    if (slow == fast) {         // change this condition to fit specific problem
        return true;
    }
}
return false;   // change return value to fit specific problem

在调用 next 字段之前，始终检查节点是否为空。

获取空节点的下一个节点将导致空指针错误。例如，在我们运行 fast = fast.next.next 之前，需要检查 fast 和 fast.next 不为空。

仔细定义循环的结束条件。

快慢指针的常见算法

快慢指针一般都初始化指向链表的头结点 head，前进时快指针 fast 在前，慢指针 slow 在后，巧妙解决一些链表中的问题。

1、判定链表中是否含有环

这属于链表最基本的操作了，学习数据结构应该对这个算法思想都不陌生。

单链表的特点是每个节点只知道下一个节点，所以一个指针的话无法判断链表中是否含有环的。

如果链表中不含环，那么这个指针最终会遇到空指针 null 表示链表到头了，这还好说，可以判断该链表不含环：

但是如果链表中含有环，那么这个指针就会陷入死循环，因为环形数组中没有 null 指针作为尾部节点。

经典解法就是用两个指针，一个跑得快，一个跑得慢。如果不含有环，跑得快的那个指针最终会遇到 null，说明链表不含环；如果含有环，快指针最终会超慢指针一圈，和慢指针相遇，说明链表含有环。

boolean hasCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;

        if (fast == slow) return true;
    }
    return false;
}

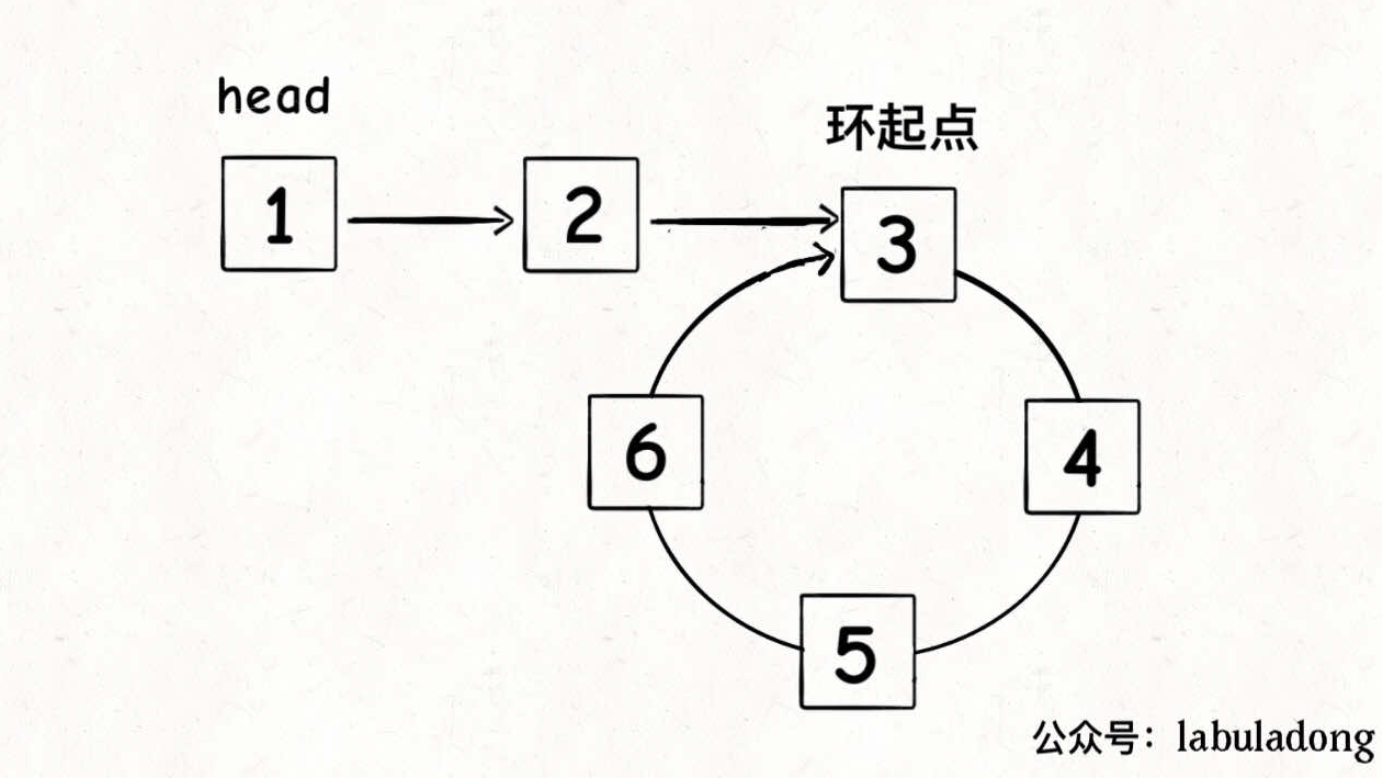
2、已知链表中含有环，返回这个环的起始位置

ListNode detectCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) break;
    }
    // 上面的代码类似 hasCycle 函数
    if (fast == null || fast.next == null) {
        // fast 遇到空指针说明没有环
        return null;
    }

    slow = head;
    while (slow != fast) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

第一次相遇时，假设慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步：

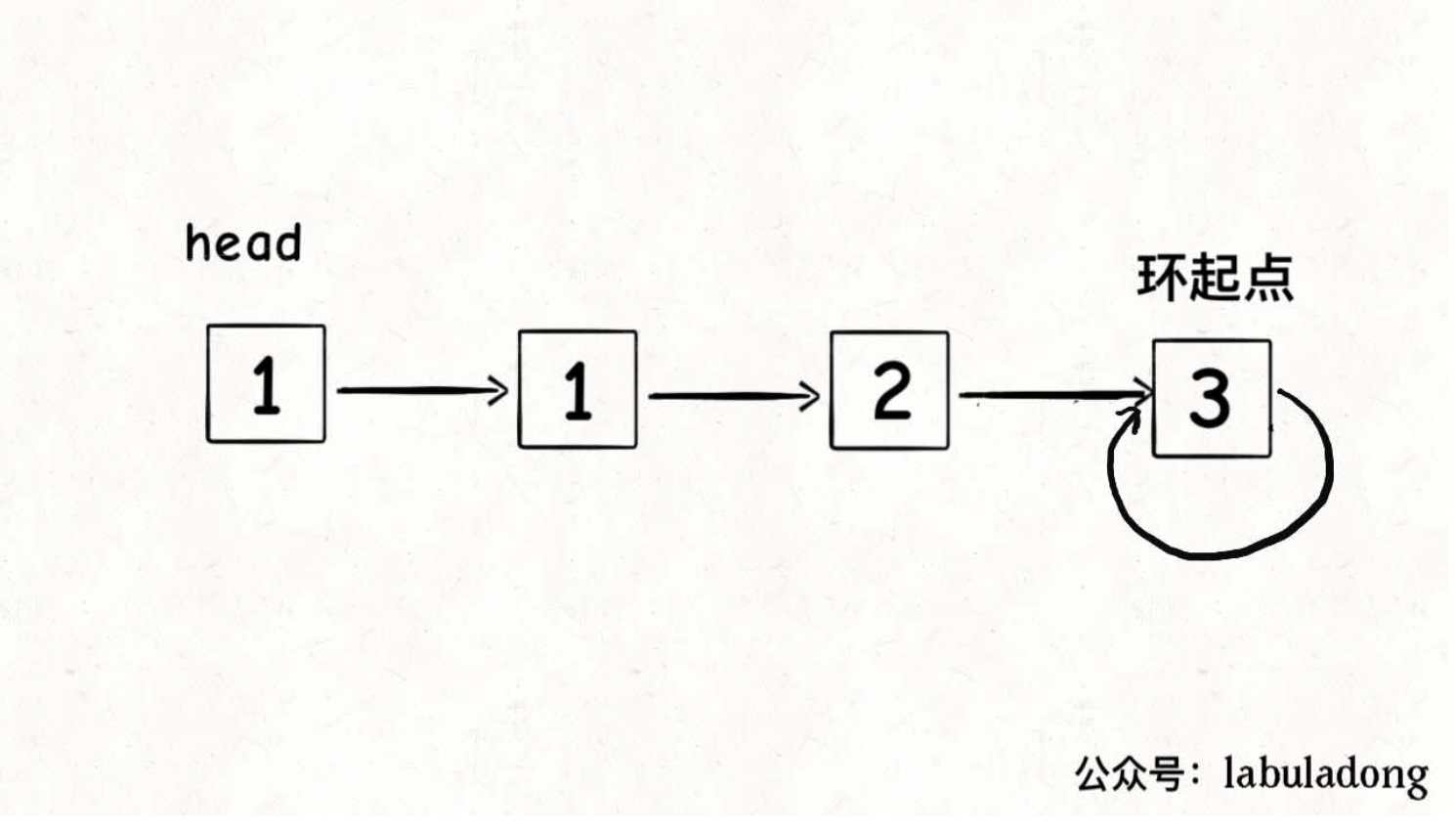
fast 一定比 slow 多走了 k 步，这多走的 k 步其实就是 fast 指针在环里转圈圈，所以 k 的值就是环长度的「整数倍」。

设相遇点距环的起点的距离为 m，那么环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。

巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。你甭管 fast 在环里到底转了几圈，反正走 k 步可以到相遇点，那走 k - m 步一定就是走到环起点了：

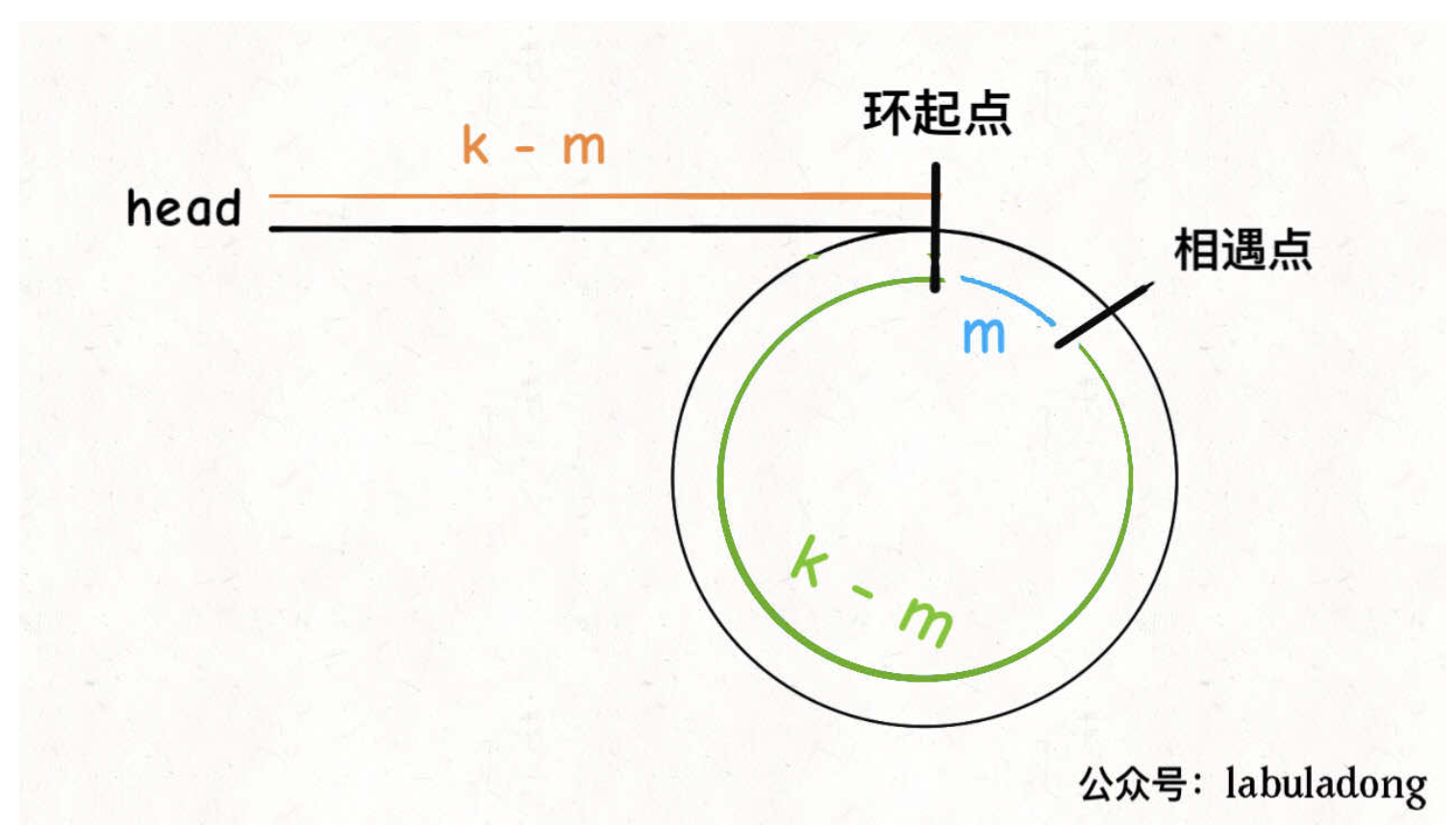
所以，只要我们把快慢指针中的任一个重新指向 head，然后两个指针同速前进，k - m 步后就会相遇，相遇之处就是环的起点了。

链表中的快慢指针

大致思路就是这样的。有几个细节还需要捋一捋。
快慢指针

这里解释一下：

只要快指针还能往下走，就继续往下走。
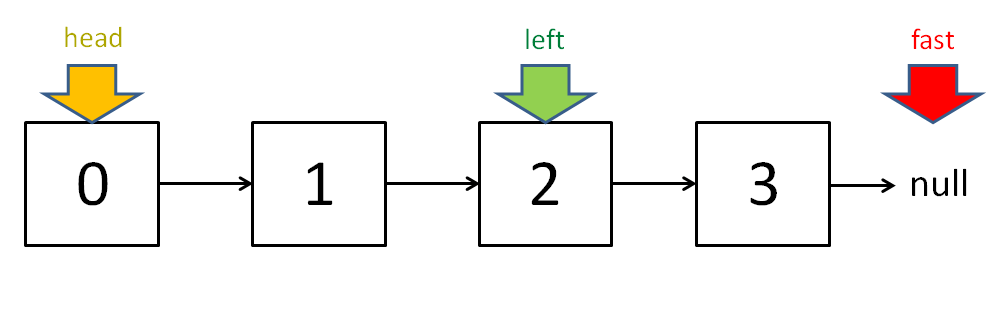
- 所以在图中偶数次的情况，slow在中间偏右
- 所以在图中奇数次的情况，slow在正中间
当快指针遍历结束时，其next节点不为空，说明有链表的size是偶数个，这时候中间节点有两个
当快指针遍历结束时，其next节点为空，说明链表的size是奇数个，这时候中间节点只有一个

当链表的长度是奇数时，slow 恰巧停在中点位置；如果长度是偶数，slow 最终的位置是中间偏右：

寻找链表中点的一个重要作用是对链表进行归并排序。

回想数组的归并排序：求中点索引递归地把数组二分，最后合并两个有序数组。对于链表，合并两个有序链表是很简单的，难点就在于二分。

但是现在你学会了找到链表的中点，就能实现链表的二分了。关于归并排序的具体内容本文就不具体展开了。